Кластер 3– V2, V4, V6 высокие «экономные покупатели».
Кластерный анализ
13.1. Кластерный анализ представляет собой класс методов, используемых для классификации объектов или событий в относительно однородные группы, которые называют кластерами.
Например: Проведено исследование покупателей по двум переменным: ориентация на качество (переменная 1), и чувствительность к цене (переменная 2).
На рис.1. представлена идеальная ситуация для кластеризации.
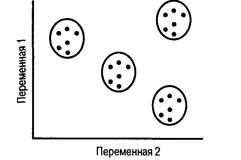
Рис.1. Идеальная ситуация для кластеризации
На практике чаще всего встречается другая ситуация (рис.2.)
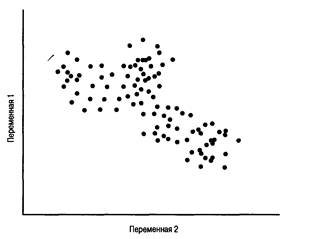
Рис.2. Реальная ситуация кластеризации
Кластерный анализ используется в маркетинге для следующих целей:
- Сегментация рынка. Например, потребителей можно разбить на кластеры на основе выгод, которые они ожидают получить от покупки данного товара.
- Понимание поведения покупателей. Кластерный анализ используют для идентификации однородных групп покупателей.
- Определение возможностей нового товара. Кластеризацией торговых марок и товаров можно определить конкурентоспособные наборы в пределах данного рынка. Торговые марки в одном и том же кластере конкурируют более жестко между собой, чем с марками других кластеров.
13.2. Этапы выполнения кластерного анализа
1. Формулировка проблемы
2. Выбор меры рассеяния
3. Выбор метода кластеризации
4. Принятие решения о количестве кластеров
5. Интерпретация и профилирование кластеров
6. Оценка достоверности кластеризации
Формулировка проблемы
Задача состоит в том, чтобы выбранный набор переменных смог описать сходство между объектами с точки зрения признаков, имеющих отношение к данной проблеме.
Выбор меры рассеяния
Заключается в выборе способа измерения расстояния или меры сходства. Наиболее часто в качестве меры сходства используется расстояние между объектами. Объекты с меньшими расстояниями между собой больше похожи, чем объекты с большими расстояниями.
Существует несколько способов вычислить расстояние между объектами:
- Эвклидово расстояние
 А (х1, у1) В(х2, у2)
А (х1, у1) В(х2, у2)
.В
 d = |AB| =
d = |AB| = 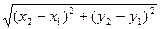 . А
. А
- Расстояние городских кварталов или Манхэттенское расстояние
d = |x2 – x1| + | y2 – y1|
Если переменные измерены в различных единицах, то перед кластеризацией их необходимо нормализовать.
Выбор метода кластеризации
Методы кластеризации могут быть иерархическими и неиерархическими.
Иерархические методы могут быть агломеративными (объединяющими) и дивизивными (разделяющими).
Агломеративная кластеризация начинается с каждого объекта в отдельном кластере. Кластеры объединяют, группируя объекты каждый раз во все более и более крупные кластеры. Этот процесс продолжается до тех пор, пока все объекты не станут членами одного кластера.
Дивизивная кластеризация начинается со всех объектов, сгруппированных в единственном кластере. Кластеры делят до тех пор, пока каждый объект не окажется в отдельном кластере.
Обычно в маркетинговых исследованиях используются агломеративные методы, например, методы связи, дисперсионные и центроидные данные.
Методы связи включают методы «ближайшего соседа», «далекого соседа» и «среднего расстояния» (Рис.3).
Метод «ближайшего соседа» (одиночная связь) первыми объединяют два объекта, расстояние между которыми минимально. Далее определяют следующее по величине самое короткое расстояние, и в кластер с первыми двумя объектами вводят третий объект. Расстояние между кластерами – расстояние между их ближайшими точками.
В методе «далекого соседа» (полная связь) расстояния между кластерами вычисляют как расстояния между их самыми удаленными точками
В методе «среднего расстояния» расстояние между кластерами определяют, как среднее значение всех расстояний между объектами двух кластеров.
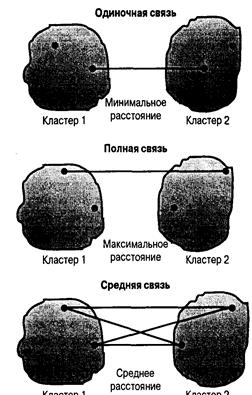
Рис.3. Методы связи для процедуры кластеризации.
В центроидных методах (Рис.4) расстояние между двумя кластерами представляет собой расстояние между их центороидами (средними).
Дисперсионные методы формируют кластеры таким образом, чтобы минимизировать внутрикластерную дисперсию. Один из них – метод Варда (Рис.4.).
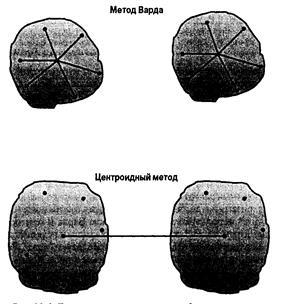
Рис.4. Центроидный метод и метод Варда
Наилучшие результаты у метода средней связи и Варда.
Неиерархические методы кластеризации ( к – средних)
Последовательный пороговый метод – выбирают центр кластера и все объекты, находящиеся в пределах заданного от центра порогового значения, группируют вместе. Затем выбирают новый кластерный центр, и процесс повторяют для несгруппированных точек.
Параллельный пороговый метод работает аналогично, выбирают несколько кластерных центров и объекты в пределах порогового уровня группируют с ближайшим центром.
Недостатки неиерархических методов:
- Число кластеров определяется заранее и выбор кластерных центров происходит независимо.
- Многие неиерархические методы выбирают первые к случаев ( к – число кластеров) и зависят от порядка наблюдений.
Пример. В табл.1 представлены данные опроса об отношении потребителей к посещению магазинов для покупки товаров. Маркетологи определили шесть переменных:
V1 – посещение магазина для покупки товаров – приятный процесс;
V2 – посещение магазинов для покупки товаров плохо сказывается на вашем бюджете;
V3 – я совмещаю посещение магазинов для покупки товаров с питанием вне дома;
V4 – я стараюсь сделать лучшие покупки при посещении магазинов;
V5 – мне не нравится посещение магазинов для покупки товаров;
V6 – вы можете сэкономить много денег, сравнивая цены в разных магазинах.
Степень согласия выражалась по семибальной шкале (1 – полностью не согласен, 7 – полностью согласен).
Таблица 1. – Данные для кластеризации
| Номер респондента | V1 | V2 | V3 | V4 | V5 | V6 |
Результаты иерархической кластеризации представлены в табл.2. Первая строка плана агломерации – первая стадия, на которой объединены респонденты 14 и 16.
Расстояние между кластерами – квадрат эвклидова расстояния между точками.
Цифра (входа в кластер 1) на стадии 7 указывает на то, что респондента 14 впервые включили в кластер на стадии 1. Последняя колонка «Следующая стадия», показывает стадию, на которой другой случай (респондент) или кластер объединили с этим кластером.
Таблица 2. – Результаты иерархической кластеризации
План агломерации на основании метода Варда
| Объединяемые кластеры | Стадия, на которой впервые появился кластер | |||||
| Стадия | Кластер 1 | Кластер 2 | Коэффициент (расстояние между кластерами) | Кластер 1 | Кластер 2 | Следующая стадия |
| 1,0 | ||||||
| 2,5 | ||||||
| 4,0 | ||||||
| 5,5 | ||||||
| 7,0 | ||||||
| 8,5 | ||||||
| 10,17 | ||||||
| 12,67 | ||||||
| 15,25 | ||||||
| 18,25 | ||||||
| 22,75 | ||||||
| 27,5 | ||||||
| 32,7 | ||||||
| 40,5 | ||||||
| 51,0 | ||||||
| 63,125 | ||||||
| 78,29 | ||||||
| 171,29 | ||||||
| 330,45 |
Древовидная диаграмма (дендрограмма) – графическое отображение результатов кластеризации (Рис.5). Вертикальные кластеры показывают кластеры, объединяемые вместе. Таблица 3 содержит данные о кластерной принадлежности объектов (два, три, четыре кластера).
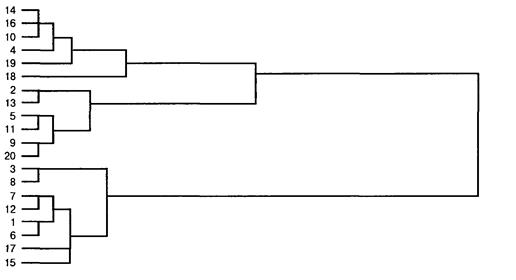
Рис. 5. Древовидная диаграмма, используемая в методе Варда
Таблица 3. - Принадлежность кластеру при использовании метода Варда
| Число кластеров | |||
| Метка (номер) случая | |||
Принятие решения о числе кластеров.
- В иерархической кластеризации в качестве критерия можно использовать расстояния, при которых объединяют кластеры (при переходе от 17 к 18 стадии коэффициент расстояния увеличивается более, чем вдвое).
- Относительные размеры кластеров должны быть достаточно выразительными.
Три кластера: 8, 6, 6 элементов
Четыре кластера: 8, 6, 5, 1.
Интерпретация и профилирование кластеров.
Включает проверку кластерных центроидов (табл. 4).
Кластер 1 – высокие значения V1, V3, низкое V5 «любители посещать магазин и делать покупки»;
Кластер 2 – высокое - V5, V1 V3 - низкие «апатичные покупатели»;
Кластер 3– V2, V4, V6 высокие «экономные покупатели».
Таблица 4. – Кластерные центроиды
| Средние переменных | ||||||
| Номер кластера | V1 | V2 | V3 | V4 | V5 | V6 |
| 5,750 | 3,625 | 6,000 | 3,125 | 1,750 | 3,875 | |
| 1,667 | 3,000 | 1,833 | 3,500 | 5,500 | 3,333 | |
| 3,500 | 5,833 | 3,333 | 6,000 | 3,500 | 6,000 |
Оценка надежности и достоверности
1. Применять различные способы измерения расстояния и сравнить результаты;
2. Использовать разные методы и сравнить результаты.
Применение неиерархической кластеризации к=3 (табл.5) по методу оптимизирующего распределения дает аналогичные результаты.
Таблица 5. – Результаты неиерархической кластеризации
| Исходные кластерные центры | ||||||
| Кластер | V1 | V2 | V3 | V4 | V5 | V6 |
| Классификационные кластерные центры | ||||||
| Кластер | V1 | V2 | V3 | V4 | V5 | V6 |
| 3,8135 | 5,8992 | 3,2522 | 6,4891 | 2,5149 | 6,6957 | |
| 1,857 | 3,0234 | 1,8327 | 3,7864 | 6,4436 | 2,5056 | |
| 6,3558 | 2,8356 | 6,1576 | 3,6736 | 1,3047 | 3,2010 |
Дата добавления: 2016-05-05; просмотров: 1953;
