Основні поняття теорії інформації
Теорія інформації – це наука яка вивчає кількісні закономірності, пов’язані з отриманням, передачею, обробкою та збереженням інформації. Ці властивості притаманні ІС, в якій здійснюється обмін інформацією між різними ланками системи. Передана інформація повинна бути певним чином «закодованою»- переведена на мову спеціальних символів та сигналів.
Одним із завдань теорії інформації є знаходження найбільш оптимальних методів кодування, які дозволяють передати задану інформацію за допомогою мінімальної кількості символів. Це завдання вирішується як за відсутності так і за наявності перешкод в каналі зв’язку. Другою задачею теорії інформації є знаходження перепускної властивості каналу зв’язку для передачі інформації без затримок та перешкод.
Як об’єкт, про який передається інформація, будемо брати систему X,якавипадковим чином може знаходитися в тому чи іншому стані. Для цієї системи маємо певну ступінь невизначеності, яка залежить від кількості її можливих станів та ймовірних станів.
Як невизначена система застосовується спеціальна характеристика – ентропія Н(Х), яка обчислюється за формулою
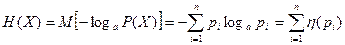 ,
,
де М- математичне сподівання;
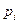 - ймовірність появи події
- ймовірність появи події 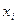 .
.
Залежно від основи логарифма а маємо різні одиниці вимірювання ентропії (а=2- в бітах; а=10- в дитах; а=е – в натах). Перехід від однієї основи логарифму до іншої здійснюється за допомогою формули
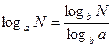 . Наприклад:
. Наприклад: 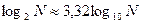
Основні властивості ентропії:
1. Вона дорівнює нулю, якщо одне з станів системи достовірне, а інші – недостовірні.
2. При заданій кількості станів вона набуває максимального значення за умови рівноймовірності цих станів ( 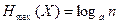 ).
).
3. Якщо декілька незалежних систем об’єднуються в одну, то їх ентропії додаються.
На практиці виникає потреба в знаходженні ентропії складної системи, об’єднавши дві чи більше простих систем. Під об’єднанням двох систем Х,У розуміється складна система (Х,У), стан якої ( 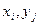 ) подає усі можливі комбінації станів систем Х,У. Знайдемо ентропію складної системи:
) подає усі можливі комбінації станів систем Х,У. Знайдемо ентропію складної системи:
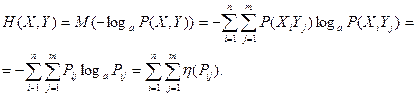
Якщо системи Х та У незалежні, то 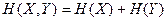 .
.
Для залежних систем маємо умовну ентропію системи У за умови, що система Х знаходиться в стані 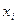 :
:
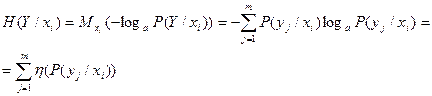
та середню або повну ентропію системи У відносно Х:
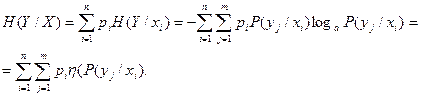
Величина 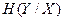 характеризує ступінь невизначеності системи У, яка залишилася після того, як стан системи Х повністю визначився.
характеризує ступінь невизначеності системи У, яка залишилася після того, як стан системи Х повністю визначився.
Теорема. Якщо дві системи Х та У об’єднуються в одну, то ентропія об’єднаної системи дорівнює ентропії однієї з іі складових частин та додатку умовної ентропії другої частини відносно першої:
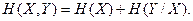
Дата добавления: 2016-05-05; просмотров: 999;
