КИНЕТИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ И УСТАЛОСТНАЯ ДОЛГОВЕЧНОСТЬ. ДОЛГОВЕЧНОСТЬ СПЛАВОВ. ДОЛГОВЕЧНОСТЬ СВАРНЫХ СОЕДИНЕНИЙ. ТЕРМООБРАБОТКА СВАРНЫХ СОЕДИНЕНИЙ И ИХ ДОЛГОВЕЧНОСТЬ.

Кинетическая теория прочности - сравнительно молодая теория. Всем хорошо знакомы методики расчета на статическую прочность и усталостную долговечность. Необоснованно прочность отождествляют с долговечностью: считается что если учтена в расчетах на прочность деградация свойств металла, то объект будет и прочным, и долговечным. Однако - и особенно это проявляется при контакте металла со средой - трещины возникают намного раньше, чем это было предположено в результате расчетов на прочность. Более того, металл, взятый на испытания непосредственно «берегов» трещины не обнаруживает резкого изменения своих механических свойств!

Это очень настораживающее обстоятельство, но оно пока еще до конца неосознанно ни конструкторами, ни прочнистами, ни эксплутацией. Этому явлению есть название - коррозионное растрескивание под напряжением (КРПН) и коррозионная усталость ( КУ). Иногда этот процесс повреждения конструкционного сплава отождествляют с водородным охрупчиванием (ВО) или с коррозией под напряжением (КПН ).

В равной степени это относится и к металлам, и к сплавам, и к сварным соединениям.

Если нет контакта со средой, то долговечность твердого тела описывается уравнением кинетической прочности:

t ~ exp( - U/ R×T ) ( 5.1 )

где U - энергия активации, и

U = E_Cв - (Ö 2) × s × NA × Q / 2 ( 5.2 )

s - механическое напряжение,

NA - число Авогадро,

Q - активационный объем.

Формулу ( 5.2 ) можно модифицировать, учтя в ней остаточное внутренние технологические напряжения. Эти напряжения напрямую обусловлены либо повышенной плотностью дислокаций, либо изменениями соотношения объемов фаз. Если с фазами еще не все ясно, то с дислокациями, как носителями информации об уровне технологической наследственности можно уже работать. Один из подходов заключается в следующем. Значение t касательных напряжений зависит от плотности дислокаций r по формуле:

t = a × G × b × 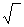r ( 5.3 )

где a - коэффициент,

G - модуль сдвига,

b - вектор Бюргера.

В этом случае (5.2 ) будет выглядеть:

U = E _Cв- [(Ö 2) × s / 2 - a × G × b × 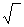r ]× NA × Q ( 5.4 )

Эта формула вместе с ( 5.1) весьма полезна при оценке долговечно-сти наклепанного металла независимо от того, как получен этот наклеп ( термической, механической или же термомеханическая обработка).

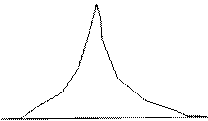
Сварное соединение представляет собой сложную систему: шов, околошовная зона, зона термического влияния. Будем анализировать распределение плотности дислокаций в обоих направлениях от зоны сплавления. Примерами может быть следующая иллюстрация рис. 5.1).

Анализируя рис. 5.1 а) 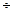г) и имея формулы (5.4 ) и ( 5.1 ) можно придти к предположению, что на рис. 5.1. а) трещина возникнет в зоне термического влияния (ЗТВ) справа от шва. Ситуацию рис. 5.1 б) можно охарактеризовать так, что ни шов, ни зоны термического влияния растрескиваются практически одновременно с основным металлом. Рис. 5.1 в) - трещина сформируется по шву. Рис. 5.1 г) - формирование трещины равновероятно и по шву и в обоих ЗТВ. Кроме того повторные «пики» плотности дислокаций могут свидетельствовать о том, что на этом удалении могут сформироваться объемы с локальной r больше средней. И в этом случае не исключена ситуация с возникновением трещины справа от шва на достаточно большом удалении от него. Увеличить долговечность можно термообработкой – нагревом и выдержкой с целью уменьшения плотности дислокаций. При прочих равных значениях влияющих факторов переход от одной плотности дислокаций r₁ к другой r₂ увеличение долговечности можно рассчитать по формуле:

( t₂ / t₁ ) = exp [ NA × Q × ( 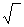r 1 - 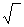r 2 )× a × G × b / R × T ] (5.5)

Усталостная долговечность металлов, сплавов и сварных соединений.

Необходимо отметить, что кинетическая прочность не широко признана специалистами из других областей занимающихся прочностью металла. Современные специалисты в области прочности всеми силами отстаивают теорию статической прочности - расчет на трещи

		Околошовная зона
		r 1/см2

ШОВ

ЗТВ

ЗТВ

Околошовная зона

а) б)

ШОВ

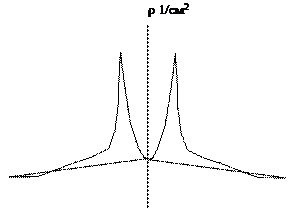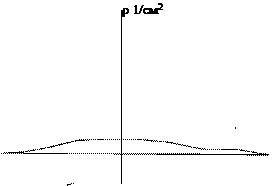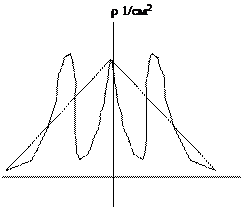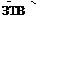в) г)

Рис.5.1

Образование трещин в сварных соединениях

нообразование через аргумент, носящий наименование коэффициента интенсивности напряжений К₁.

В усталостной долговечности есть свои новости на фоне сохранения принципа суперпозиции. Есть спектр напряжений ( дискретный ряд ) sj , отвечающих отдельным этапам нагружения металла при эксплуатации : Например s₁ - плановый разогрев; s₂ - гидроиспытания на прочность; s₃ - гидроиспытания на плотность; s₄ - расхолаживание с большими скоростями изменения температуры ( при авариях и аварийных остановах) и т. д. Каждому уровню sj отвечает допустимое число циклов нагружения N .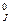

Введем понятие физически измеряемой меры повреждения. Этот термин не имеет определения по ГОСТ. Под ним предлагается понимать отношение накопленной металлом физической меры повреждения D(t) к предельно допустимой мере повреждения D_lim. С определением критерия предельного состояния мы уже сталкивались, так что МП_lim - это аналог критерия предельного состояния. Относительную меру повреждения МП (t) по определению тогда можно рассчитать по формуле

МП (t) = D(t) / D^lim (5.6 )

В переложении к циклическому нагружению

МПz(t) = å Ni / N1o (5.7 )

Если сортов циклов нагружения несколько, то используется принцип суперпозиции:

МПz(t) = åN1i / N1o + å N2i / N2o + ... = å å Nji / Njo (5.8 )

При этом обычно в пуско-наладочный период металл тоже подвергается циклическому нагружению и относительную меру повреждения его можно подсчитать можно подсчитать отдельно:

МПz = å å Nji / Njo (5.9 )

Обычно известна наработка t в течение которой достигнута относительная мера повреждения МП _Z(t).

Это необходимо для вычисления среднего темпа приращения циклической относительной меры повреждения:

a_Z = (МПz(t) - МП_Z )/ t (5.10)

Предельному состоянию металла отвечает условие:

МП_Z( t_Т ) = 1 (5.11)

где t_Т - технический ресурс.

Остаточный ресурс по условиям циклической долговечности можно вычислить как разницу между техническим ресурсом t_Т и наработкой t:

t 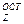= t_Т - t = (1 - МП z(t) )× t / (МП z(t) - МП z пн ) (5.12)

Формула (5.12 ) получена в предположении, что на остаточный период эксплуатации сохраняется постоянным средний темп приращения износа a_Z .

Сварное соединение необходимо подвергать контролю не только на плотность и бездефектность, но и на статическую прочность и циклическую долговечность, а также на ударную вязкость.

Типичная кривая соотношения предельного числа циклов от амплитуды нагружения s имеет форму ( рис. 5.2 ).

 

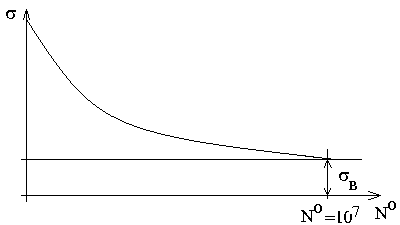
Рис. 5.2. Соотношение предельного числа циклов нагружения

металла N⁰ и амплитуды напряжений s.

Для ее построения испытываются образцы (темплеты), вырезанные из сваренного макета с соблюдением всех требований технологии. Результаты испытаний всегда будут иметь разброс. Поэтому для расчетов необходимо использовать только значения N⁰, полученные при помощи нижней огибающей (кривая 1).

Далее, может оказаться, что темплеты, вырезанные из околошовной зоны, зоны термического влияния и тела сварного шва (для крупногабаритных сварных соединений) имеют нижние огибающие, отличающиеся своей формой и числовыми характеристиками

Если произведена термообработка сварного соединения то, как пра-вило, допустимое число циклов N 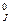увеличивается в K_T раз. (K_T>1).

Это нужно учитывать в расчетах на долговечность.

Влияние коррозионной среды - процесс сложный. В то же время специалисты по прочности рекомендуют снижать на 1 порядок ( в 10 раз) значение N .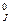

Обычно этого бывает достаточно. Но в последнее время появились весьма тревожные факты, свидетельствующие о том что нельзя одним числовым коэффициентом описать все случаи взаимодействия всех типов и марок сплавов со всеми типами коррозионных сред.

Авария на Аляске с продуктопроводом показала, что коэффициент

влияния среды может достигать 3600. Досрочная замена парогенераторов:

- за рубежом из-за коррозионного растрескивания (КР) трубных пучков ( уже

~ 200 шт, и запланировано еще около 50 шт только Франции ),

- в СНГ из-за КР коллекторов заменено 32 шт при коэффициенет влияния среды 200- 350.

Вообще говоря, не только коррозионная среда вызывает охрупчивание. Контакт циркония и его сплавов с расплавом кадмия и аустенитной стали с расплавом цинка тоже приводит к охрупчиванию конструкционных сплавов и ускоренному трещинообразованию.

В справочнике «Нормы расчета на прочность корпусов реакторов и трубопроводов» приведена уже узаконенная методика учета влияния на прочность аустенитных сталей расплавов натрия. Но натрий, калий, цинк - все-таки еще довольно уникальные, можно сказать - экзотические среды, в которых работает и металл и сварные соединения. Основной рабочей средой в подавляющем большинстве технологических процессов являются все-таки водные растворы.

Именно этому факту и будет уделено внимание в дальнейшем изложении курса.