Импульсные, релейные и цифровые САУ

Импульсными называются САУ, в которых наряду с непрерывными действуют импульсно-модулированные сигналы. Импульсно-модулированные сигналы представляют собой последовательность импульсов, у которых один или несколько параметров меняются по определенному временному закону. Такими параметрами являются:

· Амплитуда импульсов ;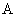

· Длительность импульса ;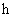

· Период повторения импульсов .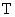

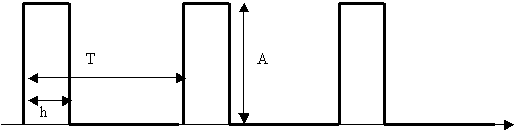
Рис. 1. Немодулированная последовательностьимпульсов

Временной закон, по которому изменяется тот или иной параметр импульсной последовательности, называется модулирующей функцией или законом модуляции. Выделяют:

· Амплитудно-импульсную модуляцию ;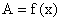

· Широтную импульсную модуляцию – ;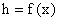

· Временную импульсную модуляцию – .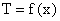

Кроме того, различают два рода модуляции импульсной последовательности. Если параметры импульсной последовательности меняются в соответствии с текущим значением модулирующей функции, то такая модуляция называется импульсной модуляцией первого рода – ИМ-1. При этом амплитуда импульсов изменяется в течение времени существования импульсов h, а длительность импульсов, их положение на оси времени, или частота определяются значением модулирующей функции в моменты времени, определенные через интервалы, в общем случае не равные периоду следования исходной, немодулированной последовательности. Пример такой модуляции показан на рис.2.

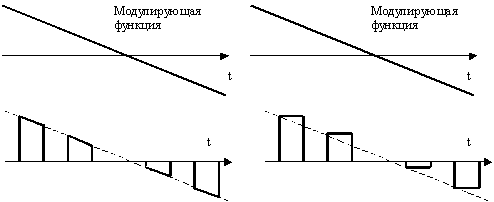
Рис. 2. Модуляция первого и второго рода

В отличие от ИМ-1 при импульсной модуляции второго рода параметры исходной последовательности изменяются в зависимости от значений модулирующей функции в фиксированные моменты времени, отстоящие друг от друга на одинаковые интервалы, равные периоду следования Т. Характер изменения сигналов при ИМ-11 показан на рис. 2.

Модуляторы, в которых осуществляется ИМ-1 или ИМ-11, в теории импульсных систем получили название импульсных элементов (ИЭ) или ключей. В зависимости от вида модуляции импульсные элементы подразделяются на амплитудные, широтные и временные (фазовые или частотные) первого и второго рода соответственно. Основными параметрами импульса является его период, длительность и форма.

В статическом режиме импульсные элементы САУ характеризуются статической характеристикой. Статической характеристикой импульсного элемента называется зависимость модулируемого параметра импульсной последовательности от дискретных значений модулирующей функции. Эти характеристики могут быть линейными и нелинейными. В частности статические характеристики широтных и частотных импульсных элементов представляют собой четные функции, а амплитудных и фазовых – нечетные функции.

Кроме импульсного элемента в состав рассматриваемого класса САУ входит непрерывная часть, во многом определяющая динамические свойства системы. В зависимости от типа и свойств импульсного элемента, а также непрерывной части импульсные САУ подразделяются на следующие виды:

Линейные импульсные САУ с постоянными параметрами – системы, у которых ИЭ и непрерывная часть линейны и содержат лишь постоянные параметры.

Линейные импульсные САУ с переменными параметрами – системы, у которых ИЭ и непрерывная часть линейны, но имеют переменные параметры.

Нелинейные импульсные САУ – системы, у которых хотя бы одна из составных частей обладает нелинейной статической характеристикой.

К линейным импульсным САУ относятся те системы, в состав которых входят амплитудный импульсный элемент и линейная непрерывная часть. Класс нелинейных импульсных САУ охватывает те системы, в состав которых входят широтные и временные ИЭ. Математические методы анализа таких систем базируются на теории разностных уравнений и методах дискретного преобразования Лапласа, с помощью которых решаются разностные уравнения.

Рис. 3. Схема импульсной системы автоматического управления

Амплитудно-импульсно-модулированные сигналы являются выходными сигналами модулятора, на вход которого поступают модулирующая функция 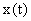и импульсная последовательность 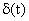. Характер модуляции определяется формой модулированных импульсов. При АИМ-1 импульсы имеют конечную длительность и в общем случае произвольную форму. На практике получение таких импульсов достигается путем использования экстраполяторов нулевого порядка, то есть устройств, которые запоминают значение модулирующей функции в начале импульса модуляции. При АИМ-11 импульсы имеют бесконечно малую длительность, так как на модулятор поступает последовательность 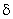— импульсов.

Теоретически более простым является случай, когда САУ содержит импульсный элемент второго типа. В то же время здесь представляется возможность раскрыть основные закономерности процессов в импульсных САУ. В этом случае выходной сигнал записывается в виде

,

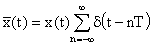где 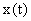– модулирующая функция,

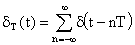— последовательность 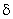-импульсов,

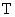– период следования 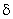-импульсов,

n – номер периода.

Представив последовательность 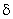-импульсов в ряд Фурье, получаем другую форму записи АИМ-11:

,

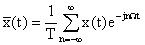где 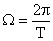– круговая частота следования импульсов.

Все многообразие способов импульсной модуляции сигналов управления представлено на рис. 4.

Под дискретным преобразованием Лапласа понимают изображение дискретных функций, задаваемых выражениями вида:

Линейной системой импульсного регулирования называется такая САУ, которая кроме звеньев описываемых обыкновенными линейными ДУ содержит импульсное звено, преобразующее непрерывное входное воздействие в равноотстоящие друг от друга по времени импульсы.

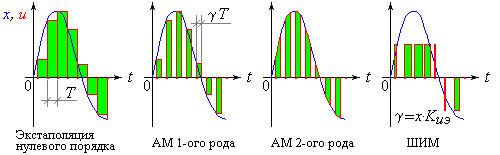
Рис. 4 Варианты выходных последовательностей импульсных звеньев

Пример простой импульсной САУ, предназначенной для управления средним значением напряжения на объекта представлен на рис. 5.

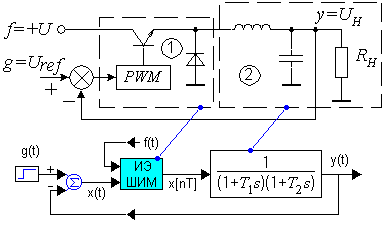
Рис. 5. Пример импульсной системы

В состав импульсной системы входят:

1 — импульсное звено — ключ с ШИМ;

2 — непрерывное звено — фильтр с нагрузкой; изменение 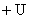можно рассматривать как возмущение .

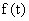Система линейна, если линеен широтно-импульсный модулятор. Если сопротивление 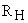меняется, то система дополнительно будет параметрической, то есть в ней присутствуют параметрические возмущения.

9.2. Математический аппарат описания импульсных систем

Для исследования импульсных систем используется дискретный математический аппарат, основным элементом которого является понятие решетчатой функции.

Решетчатой функцией 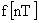или в сокращенной форме записи 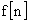, называется функция, значения которой определены в дискретные моменты времени 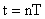, где n – целое число, а 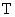– период повторения (дискретизации). Операция замены непрерывной функции решетчатой

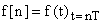
показана на рис. 6.

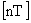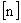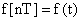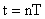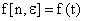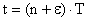Решетчатые функции такого вида определены только в дискретные моменты времени (сокращенно ), и формируются из непрерывных функций: при . Рассматривают так же смещенные решетчатые функции (последовательность 3): при , где 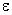— относительное смещение, .

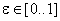9.3. Цифровые САУ

Цифровые системы строятся на базе комплекса средств вычислительной техники, основными элементами которого являются:

1. ЦВМ,

2. устройства ввода,

3. устройства вывода.

Функции ЦВМ могут выполнять:

1. ЭВМ (компьютеры),

2. DSP — цифровые сигнальные процессоры,

3. ЦУ на жесткой логике.

Первые относятся к универсальным устройствам управления, вторые специализированны для приложений, третьи разрабатываются для конкретных устройств (например, цифровой фильтр имеющийся в каждом аналогоцифровой преобразователь).

Устройствами ввода и вывода в случае состыковки с аналоговыми сигналами являются аналогоцифровые (АЦП) и цифроаналоговые (ЦАП) преобразователи, а в случае состыковки с цифровыми сигналами — порты и интерфейсы.

В системах с ЦВМ, последние могут выполнять роли:

1. регулятора,

2. регулятора и устройства сравнения,

3. корректирующего устройства,

4. самого объекта.

Если ЦВМ универсальная (ЭВМ), то возможно построение многофункциональных САУ, когда одна ЦВМ обслуживает комплекс составляющих объект устройств. Например, в станочном оборудовании:

1. стабилизации скорости механизмов подачи,

2. формировании траектории обработки,

3. управление приводом главного движения,

4. управление механизмом смены инструмента,

В подобных случаях в состав системы ЦУ должны входить аналоговые или цифровые мультиплексоры и демультиплексоры.

Во всех случаях ЦВМ предоставляет легко доступные информационные потоки, позволяющие кроме прямого управления осуществлять функции:

1. контроля,

2. оптимизации,

3. координации,

4. организации всех процессов.

9.4. Процессы протекающие в системах цифрового управления

Дискретная природа ЦВМ определила наличие 2-х процессов в системах ЦУ:

1. дискретизации сигналов по времени (получение решетчатой функции),

2. квантования сигналов по уровню (аналогоцифрового и цифроаналогового преобразования).

Дискретизация сигналов по времени делает систему дискретной, а квантование по уровню — нелинейной. Оба процесса сопровождаются возникновением методических погрешностей.

Выбор частоты дискретизации производится исходя из ширины полосы пропускания или из времени регулирования замкнутой системы. Разумные частоты дискретизации в 6..10 раз больше полосы пропускания или от 2-х до 4-х дискретных отсчетов за время нарастания, в противном случае качество системы будет резко ухудшаться.

Количество ступеней квантования по уровню оказывает существенное влияние на динамические свойства систем. При недостаточном их количестве могут возникать периодические режимы переключений между дискретами (автоколебания).

Может случиться так, что выполняемые ЦВМ задачи (опрос датчиков, расчет программы, формирование информационных потоков, запись в порты вывода) могут быть выполнены только при систематической задержке синтезируемого воздействия на один такт дискретизации. В таком случае в системе с ЦВМ появится запаздывание 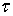, которое должно быть учтено оператором запаздывания 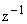и, возможно, смещенной передаточной функции .

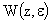Обычно количество ступеней квантования по уровню велико, поэтому его влиянием пренебрегают. Это делает систему, линейной и позволяет использовать математический аппарат импульсных систем.

9.5. Методика вывода дискретных передаточных функций

Общая схема цифровой системы представлена на рис. 1

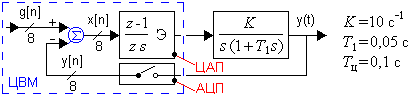
Рис. 1. Структурная схема цифровой САУ

Работу ЦВМ обеспечивают аналогоцифровой (квантователь) и цифроаналоговый (экстраполятор нулевого порядка) преобразователи, следовательно:

.

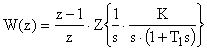Для нахождения 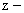изображения непрерывной передаточной функции 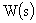по таблицам, последнюю надо разложить на элементарные дроби (т.е. преобразовать к параллельной структуре):

,

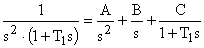где:

;

.

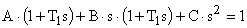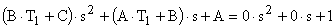Следовательно

; ; .

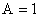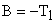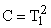Исходя из этого получаем, что

.

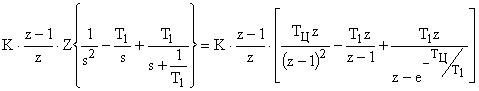Для параметров заданной системы

.

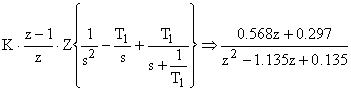Следовательно передаточная функция системы определяется как:

.

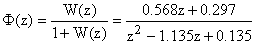9.6. О синтезе систем с ЦВМ методом ЛЧХ

Для решения проблемы синтеза цифровых САУ рассмотрим ее расчетную схемы, представленную на рис. 2.

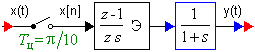
Рис. 2. Расчетная схема цифровой САУ

Изображенный дискретный фильтр имеет в области частот ЛАЧХ и ЛФЧХ периодические составляющие, как показано на рис. 3. Поэтому, использовать такой способ определения частотных характеристик САУ при синтезе ее параметров неудобно.

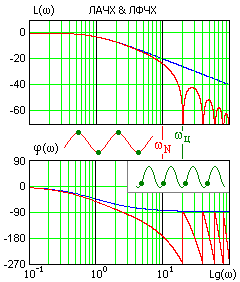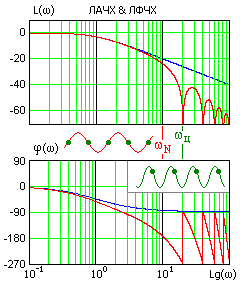
Рис. 3. Логарифмические характеристики цифровой САУ

Перевод с помощью 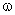— преобразования частотных характеристик в область псевдочастот 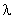, позволяет получить ЛАЧХ, которые по виду подобны ЛАЧХ непрерывных систем.

При этом используется следующая последовательность преобразований:

.

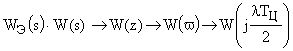Эти преобразования при использовании экстраполятора нулевого порядка могут быть формализованы. Пусть передаточная функция непрерывной части имеет вид:

.

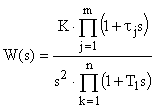Техническая реализуемость систем с ЦВМ позволяет ввести положения:

1. Пусть для частоты среза непрерывной части выполняется условие .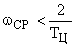

2. Все постоянные времени знаменателя разделим на две группы — до и после диапазона от частоты среза до частоты дискретизации: .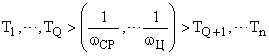

3. Постоянные времени в числителе 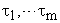пусть больше чем .

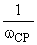4. Поскольку система должна быть устойчива, пусть наклон ЛАЧХ на 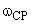будет –20 дБ/дек.

Принятые положения, позволяют описать свойства систем в области низких и высоких частот двумя передаточными функциями:

В области низких частот

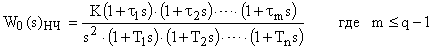
В области высоких частот

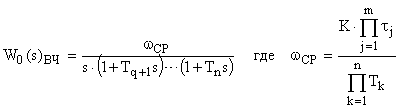
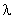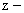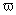Теперь для формального перехода в область псевдочастот (минуя промежуточные и -преобразования) достаточно подставить в передаточной функции 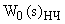вместо 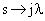и умножить ее на множитель 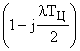, для низких частот приближенно равный 1.

А передаточная функция 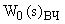будет соответствовать выражение:

,

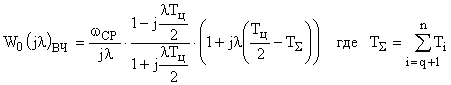Модуль которого:

.

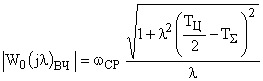Результирующий фазовый сдвиг обеих областей определяется следующим выражением:

.

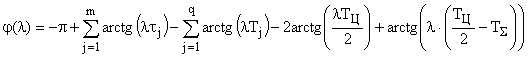Из вышесказанного можно сделать следующие выводы:

1. В области низких частот 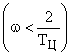асимптотическая ЛАЧХ системы с ЦВМ практически сливается с ЛАЧХ непрерывной части (множитель 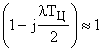) и можно положить 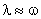. Это позволяет один к одному использовать разработанную для непрерывных систем методику формирования низкочастотной части желаемой ЛАЧХ.

2. В области высоких частот отличия вносит множитель 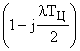, ухудшающий условия устойчивости. Поэтому при формировании запретной высокочастотной области в расчетных формулах величина 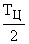должна быть просуммирована с малыми постоянными времени:

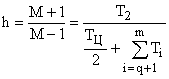
для желаемых частотных характеристик, содержащих 3 участка с наклонами –40, –20 и –40 дб/дек.

,

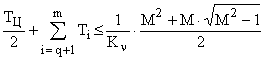где

.

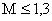Последнее выражение используется для систем, желаемые частотные характеристики имеют два участка с наклонами –20 и –40 дб/дек.