Коррекция работы САУ

Когда устойчивость и необходимое качество переходных процессов САУ не могут быть достигнуты простым изменением параметров (коэффициентов передачи, постоянных времени), тогда эта задача решается введением в систему дополнительных устройств, называемых корректирующими.

Корректирующие устройства (КУ) могут изменить не только параметры системы, но и передаточные функции, обеспечивая, тем самым, целенаправленный синтез структурных схем САУ. КУ представляют собой дополнительные звенья со свойствами настройки на типовые передаточные функции.

По способу включения КУ выделяют 3 вида коррекции САУ: последовательная, встречно-параллельная и согласно-параллельная.

Последовательная коррекция предусматривает включение корректирующего звена W_k(P) последовательно с участком структуры САУ, подлежащим перестройке W₀, для получения эквивалентной передаточной функции W_э(P)

W_э(P)=W₀(P)×W_k(P). (1.8.8)

Для получения коррекции необходимо включить звено с передаточной функцией

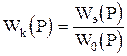. (1.8.9)

Параллельная коррекция может быть встречно-параллельная и согласно-параллельная.

Встречно-параллельная коррекция имеет эффект отрицательной обратной связи

. (1.8.10)

При . (1.8.11)

Согласно-параллельная прямая коррекция дает передаточную функцию

W_э=W₀-W_k. (1.8.12)

при отрицательном знаке корректирующего сигнала.

Моделирование САУ

За последнее время для исследования систем автоматического регулирования и, в частности, для построения переходных процессов широко применяются вычислительные машины непрерывного и дискретного действий. Наибольшее применение находят вычислительные машины непрерывного действия, относящиеся к классу моделирующих установок электронного и электромеханического типа.

Удобство моделирующих вычислительных машин заключается в том, что физическому процессу, протекающему в исследуемой системе регулирования, соответствует протекание в вычислительной машине (модели) некоторого другого "аналогового" процесса, описываемого теми же дифференциальными уравнениями, что и исходный процесс. Это позволяет изучать процессы в системах регулирования наиболее наглядно, так как каждой обобщенной координате в исследуемой системе соответствует некоторая переменная в вычислительной машине, например, электрическое напряжение, ток (в электронной модели) или угол поворота (в электромеханической модели).

Моделирующие вычислительные машины применяются и для сопряжения реального регулятора с объектом, в качестве которого выступает модель. Получается замкнутая система регулирования, которая может быть исследована еще до того, как будет построен сам объект.

Вычислительные машины целесообразно использовать для исследования обыкновенных линейных систем в тех случаях, когда последние описываются дифференциальными уравнениями сравнительно высокого порядка и их аналитическое исследование становится малоэффективным.

Однако наибольшее значение имеют вычислительные машины при исследовании линейных систем с переменными параметрами и нелинейных систем, поскольку для этих случаев пока еще мало разработано приемлемых для практики методов, а иногда аналитические методы вообще отсутствуют.

АВМ обычно просты и удобны, но имеют небольшую точность моделирования в пределах нескольких процентов.

Аналоговые вычислительные машины (АВМ) относятся к классу машин непрерывного действия и разделяются на следующие типы:

- электронные;

- электромеханические.

Электронные АВМ имеют наибольшее применение вследствие их сравнительной простоты в изготовлении и эксплуатации. Процессы в исследуемой системе изучаются при помощи наблюдения процессов в некоторой схеме, которая описывается теми же дифференциальными уравнениями, что и исходная.

Существуют две разновидности электронных АВМ: модели структурного вида и модели матричного вида.

Первая позволяет моделировать структурную схему системы управления, что во многих случаях оказывается более удобным и наглядным.

К АВМ структурного вида относятся: ИПТ-5, МПТ-9, МПТ-11, МН-1, МН-2, МН-7, МНМ, ЭМУ-10 и др.

Машины матричного вида (ИПТ-4), ЭЛИ-14 и др.) требуют записи дифференциальных уравнений исследуемой системы в особой, матричной форме. Матричные модели менее удобны для исследования систем управления и используются реже.

Решение задачи моделирования на АВМ структурного вида может быть осуществлено двумя способами:

1) по дифференциальному уравнению, которым описывается исследуемая система;

2) по структурной схеме исследуемой системы.

Пусть дана система регулирования с передаточной функцией и структурой рис. 1.9.1,а.

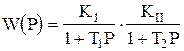. (1.9.1)

Дифференциальное уравнение замкнутой системы будет выглядеть следующим образом:

[1+W(P)]y(t)=W(P)x(t). (1.9.2)

Приведем уравнение к полиноминальному виду

(a₀P³+a₁P²+a₂P+a₃)y(t)=a₃x(t), (1.9.3)

где a₀=T₁T₂, a₁=T₁+T₂, a₂=1 и a₃=K₁K₁₁ .

Перейдем к машинным переменным и запишем дифференциальное уравнение для ввода в машину

(A₀P³+A₁P²+A₂P+A₃)Y(t)=B₀x(t) (1.9.4)

или 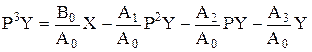. (1.9.5)

Рассмотрим цепочку из трех последовательно включенных интеграторов (рис.1.9.1,б). Если на вход первого интегратора поступает величина P³Y, то на его выходе получится с учетом перемены знака величина P²Y, на выходе второго интегратора - величина РY и на выходе третьего - Y.

В результате можно реализовать дифференциальное уравнение (1.9.5) если на входе первого интегратора сложить с учетом знаков и масштабов все члены, входящие в правую часть формулы.

Принципиальная схема электронной модели приведена на рис.1.9.1,в. Типовые звенья набраны на операционных усилителях, резисторах и конденсаторах.

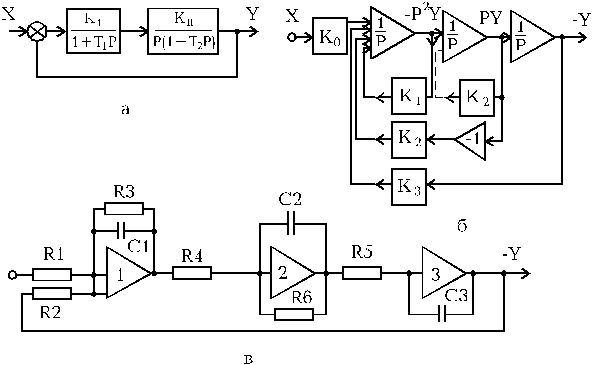
Рис.1.9.1. Моделирование на АВМ автоматической системы
регулирования:
а - структурная схема САР;
б - структурная схема электронной модели;
в - принципиальная схема электронной модели