Оптимальная линейная фильтрация непрерывных сигналов
Рассмотрим теорию оптимальной линейной фильтрации стационарных процессов – фильтр Колмогорова-Винера или оптимальный линейный фильтр (ОЛФ).
Пусть на входе линейного фильтра с передаточной функцией H(jw) действует сумма полезного сигнала s(t) и помехи n(t). Отклик фильтра на это действие – восстановленный полезный сигнал 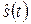 (оценка сигнала s(t)). Будем считать, что s(t) и n(t) – стационарные взаимнонекоррелированные процессы с известными спектральными плотностями мощности (СПМ) Gs(f) и Gn(f). Нужно найти такую функцию H(jw), которая обеспечивает минимум среднего квадрата ошибки восстановления сигнала
(оценка сигнала s(t)). Будем считать, что s(t) и n(t) – стационарные взаимнонекоррелированные процессы с известными спектральными плотностями мощности (СПМ) Gs(f) и Gn(f). Нужно найти такую функцию H(jw), которая обеспечивает минимум среднего квадрата ошибки восстановления сигнала
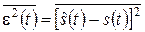 . (22.1)
. (22.1)
Иначе говоря, критерием оптимальности фильтра является минимум среднего квадрата ошибки восстановления сигнала. В такой постановке задача была решена А.Н. Колмогоровым (1939 г.) для дискретных случайных последовательностей и Н. Винером (1941 г.) для непрерывных процессов. Поэтому оптимальный (в указанном смысле) линейный фильтр называется фильтром Колмогорова-Винера.
Действующие на входе фильтра сигнал s(t) и помеха n(t) проходят через фильтр независимо и создают на выходе фильтра соответственно фильтрованные сигнал sвых(t) и помеху nвых(t). С учетом этого ошибка восстановления запишется
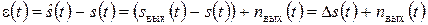 . (22.2)
. (22.2)
Слагаемое Ds(t) отражает составляющую ошибки, обусловленную линейными искажениями полезного сигнала фильтром. Средний квадрат ошибки 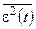 запишется
запишется
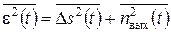 . (22.3)
. (22.3)
Величина линейных искажений полезного сигнала фильтром 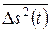 зависит от степени отличия АЧХ фильтра от постоянной величины и степени отличия ФЧХ от линейной зависимости. Средний квадрат шума
зависит от степени отличия АЧХ фильтра от постоянной величины и степени отличия ФЧХ от линейной зависимости. Средний квадрат шума 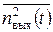 на выходе фильтра зависит только от АЧХ фильтра. Для того чтобы линейные искажения полезного сигнала были минимальными, ФЧХ фильтра должна быть линейной
на выходе фильтра зависит только от АЧХ фильтра. Для того чтобы линейные искажения полезного сигнала были минимальными, ФЧХ фильтра должна быть линейной
j(w) = –wt0, (22.4)
где t0 – задержка сигнала в фильтре. Ясно, что с учетом задержки соотношение (22.1) имеет вид 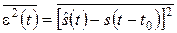 . Это уточнение не влияет на критерий оптимальности, поскольку в системах связи и вещания ожидаемая задержка сигнала в фильтре несущественная.
. Это уточнение не влияет на критерий оптимальности, поскольку в системах связи и вещания ожидаемая задержка сигнала в фильтре несущественная.
Перейдем к определению АЧХ фильтра. Для этого определим спектральные плотности мощностей левой и правой частей соотношения (22.2)
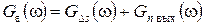 . (22.5)
. (22.5)
Выразим СПМ помехи на выходе фильтра через СПМ помехи n(t) и искомую АЧХ фильтра:
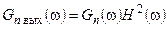 . (22.6)
. (22.6)
По определению СГП ергодичного процесса
 , (22.7)
, (22.7)
где SDs(w) – амплитудный спектр ошибки за счет линейных искажений Ds(t);
Т – длительность реализации Ds(t).
Поскольку амплитудный спектр сигнала sвых(t) определяется как S(w)×H(w), где S(w) – амплитудный спектр сигнала s(t), то
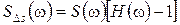 . (22.8)
. (22.8)
Переходя от амплитудных спектров к СПМ, получим
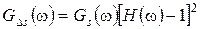 . (22.9)
. (22.9)
После подстановки соотношений (22.6) и (22.9) в (22.5) получим
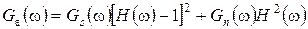 . (22.10)
. (22.10)
Средний квадрат ошибки восстановления (средняя мощность) вычисляется
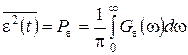 . (22.11)
. (22.11)
Поскольку функция Ge(w) ³ 0 на всех частотах, то, обеспечив min Ge(w) на всех частотах, достигнем минимума величины 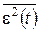 . Искомую АЧХ H(w) определим из условия экстремума функции Ge(w):
. Искомую АЧХ H(w) определим из условия экстремума функции Ge(w):
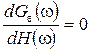 ; (22.12)
; (22.12)
 . (22.13)
. (22.13)
После решения уравнения (22.13) получим выражение для АЧХ фильтра
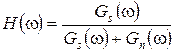 . (22.14)
. (22.14)
На рис. 22.1 иллюстрируется АЧХ ОЛФ, определенная соотношением (22.14).
Из рис. 22.1 видно особенности АЧХ ОЛФ:
- на частотах, где Gn(f) = 0, значение АЧХ H(f) = 1 – в этих областях частот фильтр не должен вносить искажений;
- на частотах, где Gs(f) = 0, значение АЧХ H(f) = 0 – в этих областях частот фильтр должен полностью ослаблять составляющие помехи;
- на частотах, на которых Gs(f) = Gn(f), АЧХ H(f) = 0,5;
- на других частотах значения АЧХ определяются вычислениями по формуле (22.14).
Подставим выражение (22.14) в соотношение (22.10) для определения СПМ ошибки:
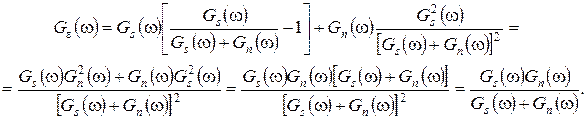 (22.15)
(22.15)

При подстановке соотношения (22.15) в выражение (22.11) можно вычислить средний квадрат ошибки восстановления сигнала 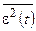 .
.
Из (22.15) видно, что ошибка 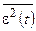 равна нулю только в том случае, когда Gs(f)Gn(f) = 0, т.е. когда спектры сигнала и помехи не перекрываются (хотя бы один с сомножителей равен нулю).
равна нулю только в том случае, когда Gs(f)Gn(f) = 0, т.е. когда спектры сигнала и помехи не перекрываются (хотя бы один с сомножителей равен нулю).
Перепишем соотношение (22.14) в виде
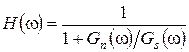 . (22.16)
. (22.16)
Из последнего соотношения видно, что коэффициент передачи оптимального фильтра на каждой из частот тем меньше, чем больше отношение Gn(f)/Gs(f) на этой частоте.
Следует отметить, что оптимальные линейные фильтры, обеспечивающие минимум ошибки 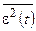 , существенным образом отличаются от согласованных фильтров, рассмотренных ранее. Если основное назначение рассмотренных здесь фильтров состоит в наилучшем воспроизведении формы сигнала, то задача согласованных фильтров состоит в формировании максимального отношения сигнал/шум в момент отсчета.
, существенным образом отличаются от согласованных фильтров, рассмотренных ранее. Если основное назначение рассмотренных здесь фильтров состоит в наилучшем воспроизведении формы сигнала, то задача согласованных фильтров состоит в формировании максимального отношения сигнал/шум в момент отсчета.
При использовании ОЛФ в аналоговых системах связи и вещания выявляется такая особенность. Имеет место высокое отношение спектральных плотностей сигнала и шума: Gs(f)/Gn(f) >> 1. Выражение для АЧХ ОЛФ (22.14) в случае полосовых сигналов переходит в следующее
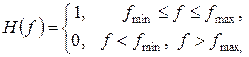 (22.17)
(22.17)
где fmin и fmax – граничные частоты спектра сигнала. В случае НЧ сигналов
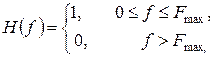 (22.18)
(22.18)
где Fmax – максимальная частота спектра сигнала.
Таким образом, оптимальные линейные фильтры в системах связи и вещания имеют П-образную АЧХ.
Контрольные вопросы
1. Сформулируйте критерий оптимальности ОЛФ.
2. При каком условии ошибку восстановления сигнала можно свести к нулю?
3. Объясните отличие ОЛФ и согласованного фильтра с точки зрения ослабления помех.
Дата добавления: 2016-06-02; просмотров: 1613;
