ВЫЯВЛЕНИЕ ОСНОВНОЙ ТЕНДЕНЦИИ РЯДА ДИНАМИКИ
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития.
При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы. Одним из приемов выявления основной тенденции является метод укрупнения интервалов. Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.
Для каждого образованного таким образом периода рассчитывается свой показатель уровня ряда: либо простым суммированием уровней первоначального ряда, либо их усреднением. При вычислении этих показателей отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживается действие основных факторов. Сравнивая их за различные (укрупненные) интервалы времени, можно выявить направление и характер (ускорение или замедление роста) основной тенденции развития.
Другой прием – метод скользящей средней. Суть метода скользящей средней состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
Для определения скользящей средней формируют укрупненные интервалы, состоящие из одинакового числа уровней — L. Каждый последующий интервал получаем, сдвигаясь на один уровень влево. Первоначальный интервал будет включать уровни Y0, Y1,...YL, второй — Y1, Y2, ... YL+1 и т.д. Таким образом, интервал сглаживания как бы скользит по динамическому ряду с шагом, равным единице. По сформированным укрупненным интервалам определяем среднее значение. Полученная средняя относится к середине укрупненного интервала. Поэтому при сглаживании скользящей средней технически удобнее укрупненный интервал составлять из нечетного числа уровней ряда. При использовании приема скользящей средней сглаженный ряд сокращается по сравнению с исходным рядом на число уровней, равное
L-1, т.е. происходит потеря информации. Вместе с тем чем продолжительнее интервал сглаживания, тем сильнее усреднение, а потому выявляемая тенденция развития получается более плавной. Чаще всего интервал сглаживания берут равным 3,5,7 уровням.
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание.
Аналитическое выравнивание – это описание основной тенденции количественной моделью. При этом уровни ряда динамики выражаются в виде функции времени:
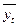 = f(t).
= f(t).
Для выравнивания ряда динамики по прямой (на основе линейной функции) используется уравнение:
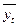 = a
= a  + a
+ a 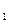 t;
t;
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров a  и a
и a 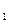 :
:
 a
a  n + a
n + a 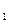
 t =
t =  y;
y;
a 
 t + a
t + a 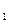
 t² =
t² =  ty,
ty,
где y – исходный уровень ряда динамики;
n –число членов ряда;
t – показатель времени, который обозначается порядковыми номерами, начиная от низшего.
Решение системы уравнений позволяет получить выражения для параметров a  и a
и a 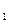 :
:
a  =
=  ;
;
a 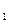 =
= 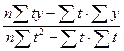 .
.
Для выравнивания ряда динамики на основе параболы второго порядка используется уравнение:
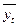 = a
= a  + a
+ a 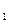 t+ a
t+ a 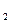 t
t 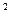 (при
(при 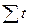 = 0):
= 0):
a  =
= 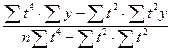 ;
;
a 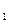 =
= 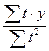 ;
;
a 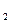 =
= 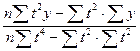 .
.
Дата добавления: 2016-06-02; просмотров: 727;
