ОПРЕДЕЛЕНИЕ ТЕСНОТЫ КОРРЕЛЯЦИОННОЙ СВЯЗИ
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента.
В статистической теории разработаны и на практике применяются различные модификации формул расчета данного коэффициента:
.
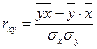Произведя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
.
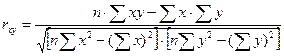Линейный коэффициент корреляции может быть также выражен через дисперсии слагаемых:
.
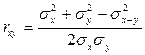Между линейным коэффициентом корреляции и коэффициентом существует определенная зависимость, которую можно математически выразить следующей формулой:
,
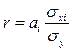где 
- коэффициет регрессии в уравнении связи;
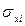- среднее квадратическое отклонение соответствующего факторного признака.
Область допустимых значений линейного коэффициента корреляции от -1 до +1. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно представить в таблице 9.1:
Таблица 9.1 - Оценка линейного коэффициента корреляции.
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |
| r = 0 | Отсутствует | |
| 0 < r < 1 | Прямая | С увеличением X увеличивается Y |
| -1 < r < 0 | Обратная | С увеличением X уменьшается Y, и наоборот |
| r = 1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного признака |
Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента:
.
Если расчетное значение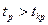 
(табличное), то гипотеза 
отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической зависимости между x и y.
Дата добавления: 2016-06-02; просмотров: 650;