РЯДЫ РАСПРЕДЕЛЕНИЯ И ИХ ХАРАКТЕРИСТИКИ.
Результаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических рядов распределения и таблиц.
После определения группировочного признака и границ групп строится ряд распределения.
Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он характеризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.
Ряды распределения, построенные по атрибутивным признакам, называются атрибутивными. Примером атрибутивных рядов могут служить распределения населения по полу, занятости, национальности, профессии и т. д.
Ряды распределения, построенные по количественному признаку (в порядке возрастания или убывания наблюденных значений), называются вариационными. Например, распределение населения по возрасту, рабочих — по стажу работы, заработной плате и т. д.
Вариационные ряды распределения состоят из двух элементов: вариантов и частот.
Числовые значения количественного признака в вариационном ряду распределения называются вариантами. Они могут быть положительными и отрицательными, абсолютными и относительными. Так, при группировке предприятий по результатам хозяйственной деятельности варианты — положительные (прибыль) или отрицательные (убыток) числа.
Частоты — это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности.
Частости — это частоты, выраженные в виде относительных величин (долях единиц или процентах). Сумма частостей равна единице или 100%. Замена частот частостями позволяет сопоставлять вариационные ряды с разным числом наблюдений.
Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные. Дискретные вариационные ряды основаны на дискретных (прерывных) признаках, имеющих только целые значения (например, тарифный разряд рабочих, число детей в семье), на дискретных признаках, представленных в виде интервалов; интервальные — на непрерывных признаках (принимающих любые значения, в том числе и дробные).
При наличии достаточно большого количества вариантов значений признака первичный ряд является трудно обозримым, и непосредственное рассмотрение его не дает представления о распределении единиц по значению признака в совокупности. Поэтому первым шагом в упорядочении первичного ряда является его ранжирование, т. е. расположение всех вариантов в возрастающем (или убывающем) порядке.
Например, стаж работы (годы) 22 рабочих бригады характеризуется следующими данными: 2, 4, 5, 5, 6, 6, 5, 6, 6, 7, 7, 8, 8, 9, 10, 11, 4, 3, 3, 4, 4, 5.
Ранжированный ряд, построенный по этим данным: 2, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 8, 8, 9, 10, 11.
При рассмотрении первичных данных можно видеть, что одинаковые варианты признака у отдельных единиц повторяются (здесь и далее — частота повторения; п — объем изучаемой совокупности).
Способы построения дискретных и интервальных рядов различны.
Для построения дискретного ряда с небольшим числом вариантов выписываются все встречающиеся варианты значений признака х, а затем подсчитывается частота повторения варианта. Ряд распределения принято оформлять в виде таблицы, состоящей из двух колонок (или строк), в одной из которых представлены варианты, в другой — частоты. Построение дискретного вариационного ряда не составляет труда.
Для построения ряда распределения непрерывно изменяющихся признаков, либо дискретных, представленных в виде интервалов («от - до»), необходимо установить оптимальное число групп (интервалов), на которое следует разбить все единицы изучаемой совокупности. При группировке внутри одно-
качественной совокупности появляется возможность применения равных интервалов, число которых зависит от вариации признака в совокупности и от количества обследованных единиц.
Проиллюстрируем построение интервального вариационного ряда по данным приведенного ранее примера распределения рабочих по стажу работы.
Для нашего примера, согласно формуле Стерджесса, при N = 22 число групп п= 5. Зная число групп, определим интервал по формуле:
i = 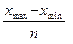 =
= 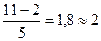 (2)
(2)
В результате получим следующий ряд распределения по стажу работы ( 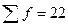 ):
):
| X | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
| F |
Как видно из данного распределения, основная масса рабочих имеет стаж работы от 4 до 8 лет.
Ряды распределения удобно изучать с помощью графического метода. Все множество графических представлений рядов распределения разделяют на два класса: линейные графики и диаграммы.
К классу линейных графиков относятся: полигон, кумулята, огива, кривая Лоренца.
Полигон применяют для дискретного ряда распределения (рисунок 3.1). Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяют прямыми линиями и получают ломаную линию, называемую полигоном частот. Для замыкания полигона крайние точки (слева и справа на ломаной линии) соединяют с точками на оси абсцисс и получают многоугольник.

Рисунок 3.1 - Полигон распределения работников строительной фирмы «Скат» по уровню дохода в январе 1998 г.
Кумулята – ломаная, составленная по накопленным частотам или частостям. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака, не больше, чем рассматриваемое значение.
При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат – накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту. Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву.
Кривой концентрации или кривой Лоренца называют кривую относительной концентрации суммарного значения признака. Она представляет собой ломаную, координатами точек которой являются на оси абсцисс накопленные относительные частоты, а на оси ординат – накопленное (нарастающим итогом) значение признака Х. Чем ближе кривая Лоренца к прямой линии, тем распределение признака более равномерное, т.е. концентрация меньше. Чем кривизна кривой больше, тем распределение более неравномерное, т.е. концентрация больше.
К классу диаграмм прежде всего относят гистограмму. Гистограмма применяется для изображения интервального ряда. При построении гистограмма на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате мы получаем гистограмму-график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для того, чтобы устранить влияние величины интервала на распределение интервала и получить возможности сравнивать частоты. Плотность распределения – это частота, рассчитанная на единицу ширины интервала, т.е. сколько единиц в каждой группе приходится на единицу величины интервала.
Дата добавления: 2016-06-02; просмотров: 1150;
