Средняя квадратическая погрешность конечной точки хода произвольной формы
В полигонометрическом ходе изогнутой формы будут иметь место невязки f’X и f’Y и невязка в периметре:
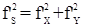 .
.
Предположим, что для одного и того же хода k раз измерены все углы и все линии. Следовательно, можно найти k значений невязок f’X, f’Y и f’S, т.е. средние значения будут равны:
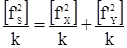 .
.
Поэтому:
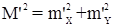 .
.
Запишем координатные условные уравнения:

 где αi – дирекционный угол линий хода;
где αi – дирекционный угол линий хода;
υЅi и υβi – поправки в измеренные значения линий и углов;
 Xn+1 - Xi, Yn+1 - Yi – разность координат между конечной и каждой точками хода;
Xn+1 - Xi, Yn+1 - Yi – разность координат между конечной и каждой точками хода;
f‘x f‘y – невязки в приращениях координат.
Учитывая, что поправка υ и ошибка d отличаются знаками

Получим,
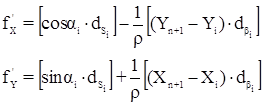
 Переходя к среднеквадратической погрешности, будем иметь
Переходя к среднеквадратической погрешности, будем иметь
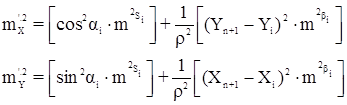
Следовательно, при mβi = mβ
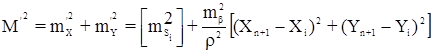
Так как

получим
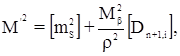
где Dn+1, i – расстояние между последней и i точками хода.
С учетом погрешностей исходных данных будем иметь
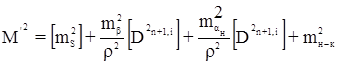
Если углы предварительно исправлены за угловые невязки, то
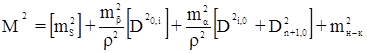 ,
,
где D0, i – расстояние между центром тяжести вершин хода и каждым его пунктом;
D1, 0 Dn+1,0 – расстояние от центра тяжести до начальной и конечной точки хода
Координаты центра тяжести вершин хода вычисляются по формуле:
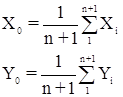 .
.
Дата добавления: 2016-06-02; просмотров: 2951;
