В произвольном направлении

Получим. Пусть колебания в плоскости, параллельной волновым поверхностям и проходящей через начало коорди­нат, имеют вид:

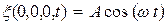(22.12)

В плоскости, отстоящей от начала координат на расстояние l , колебания будут отставать по времени на 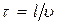. Поэтому уравнение колебаний в этой плоскости имеет вид:

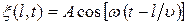(22.13)

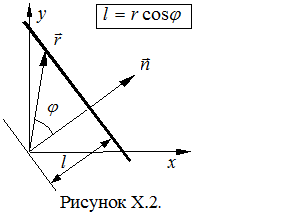
Из аналитической геометрии известно, что расстояние от начала ко­ординат до некоторой плоскости равно скалярному произведению ради­ус-вектора 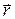некоторой точки плоскости на единичный вектор нормали 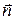к плоскости: 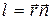. Рисунок иллюстрирует данное положение для двумерного случая. Подставим значение l в урав­нение (22.13):

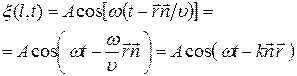(22.14)

Вектор 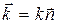, равный по модулю волновому числу и направленный по нормали к волновой поверхности, называется волновым вектором. Уравнение плоской волны можно теперь записать в виде:

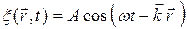. (22.15)

Функция (22.15) даёт отклонение от положения равновесия точки с радиус-вектором 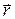в момент времени t. Для того, чтобы представить зависимость от координат и времени в явном виде необходимо учесть, что

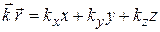. (22.16)

Теперь уравнение плоской волны принимает вид:

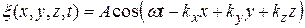. (22.17)

Часто оказывается полезным представить уравнение волны в экспоненциальной форме. Для этого воспользуемся формулой Эйлера:

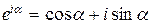, (22.18)

где 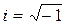, запишем уравнение (22.15) в виде:

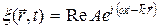. (22.19)

Волновое уравнение

Уравнение любой волны является решением дифференциального уравнения второго порядка, называемого волновым. Для того чтобы установить вид этого уравнения, найдем вторые производные по каждому из аргументов уравнения плоской волны (22.17):

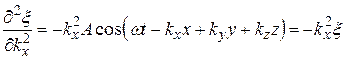, (22.20)

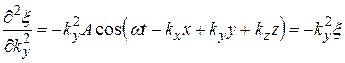, (22.21)

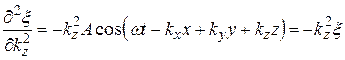, (22.22)

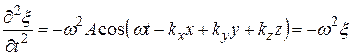. 22.23)

Сложим первые три уравнения с производными по координатам:

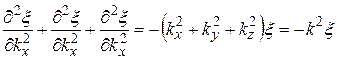. (22.24)

Выразим 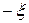из уравнения (22.23) : 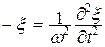, и учтем, что :

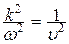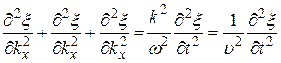(22.25)

Сумму вторых производных в левой части (22.25) представим как результат действия оператора Лапласа на 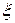, и в окончательном виде представим волновое уравнение в виде:

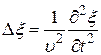(22.26)

Примечательно, что в волновом уравнении квадратный корень из величины, обратной коэффициенту при производной по времени дает скорость распространения волны.

Можно показать, что волновому уравнению (22.26) удовлетворяет любая функция вида:

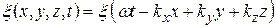, (22.27)

и каждая из них является уравнением волны и описывает некоторую волну.