КИНЕТИЧЕСКАЯ ЭНЕРГИЯ И РАБОТА ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ ТЕЛА

Рассмотрим твердое тело, вращающееся с угловой скоростью 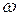вокруг некоторой оси. Считая тело состоящим из жестко связанных частиц, для кинетической энергия 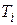некоторой частицы массой 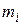, движущейся, вследствие вращения тела, с линейной скоростью 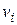можем утверждать:

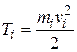(4.20)

Учитывая, что линейная скорость 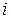-той частицы 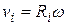, для кинетической энергии частицы находим:

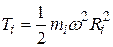(4.21)

Кинетическая энергия тела, обусловленная его вращением (!), складывается из кинетических энергий отдельных частиц:

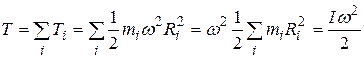(4.21)

где 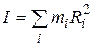- момент инерции тела.

Работа, совершаемая всеми приложенными к телу силами, идет на увеличение его кинетической энергии. Поэтому

, (4.21)

где 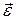есть угловое ускорение тела.

Таким образом,

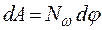(4.22)

Если внимательно сравнить формулы для вращательного и поступательного движений, то легко установить аналогию величин и формул:

Аналогия величин и соотношений поступательного и вращательного движений
Поступательном движение	Вращательное движение
Путь	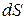Угол поворота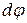
Перемещение	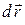Угол поворота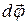
Скорость	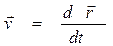Угловая скорость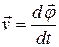
Масса	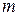Момент инерции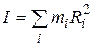
Импульс	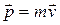Момент импульса 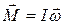(вокруг оси симметрии)
Сила	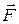Момент силы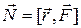
Второй закон Ньютона	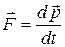Основное уравнение динамики вращательного движения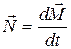
Кинетическая энергия	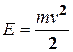Кинетическая энергия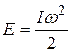
Продолжите самостоятельно	Продолжите самостоятельно