ПРЕДЕЛЬНОЕ СОПРОТИВЛЕНИЕ ГРУНТОВ СДВИГУ. УСЛОВИЯ ПРОЧНОСТИ

Под действием внешней нагрузки в отдельных точках (областях) грунта эффективные напряжения могут превзойти внутренние свя­зи между частицами грунта, возникнут скольжения (сдвиги) одних частиц или агрегатов их по другим и может нарушиться сплошность грунта в некоторой области, т. е. прочность грунта будет превзой­дена.

Внутренним сопротивлением, препятствующим перемещению (сдвигу) частиц в идеально сыпучих телах, к каким можно отнести чистые пески, будет лишь трение, возникающее в точках контакта частиц. В идеальных же связных грунтах, таких, как, например очень вязкие дисперсные глины, перемещению частиц будут сопро­тивляться только, внутренние структурные связи и вязкость водно-коллоидных оболочек частиц.

Природные же глины будут обладать как вязкими (водно-кол­лоидными), так и жесткими (кристаллизационными) внутренними связями, причем роль тех или иных связей для разных глин будет различна.

Пока эффективными напряжениями внутренние связи не преодо­лены, связный грунт будет вести себя как квазитвердое тело, обла­дающее лишь упругими силами сцепления.

Под силами сцепления мы будем подразумевать сопротивление структурных связей всякому перемещению связываемых ими частиц, независимо от величины внешнего давления.

Если нагрузка будет такова, что эффективные напряжения прев­зойдут прочность жестких структурных связей, то в точках контакта минеральных частиц и по поверхностям их водно-коллоидных (проч­но связанных с минеральными частицами) прослоек сдвижению час­тиц будут сопротивляться еще оставшиеся и вновь возникающие водно-коллоидные связи. Разделить эти сопротивления на только трение и только сцепление чаще всего не представляется возмож­ным, так как одновременно будет иметь место как трение сдвигае­мых частиц одна по другой, так и преодоление вязких сопротивле­ний, которые всегда остаются в глинистых грунтах, потому что при преодолении одних вязких связей (если жесткие связи уже раз­рушены) возникают новые.

Как показывают многочисленные опыты, сопротивление сдвигу несвязных твердых минеральных частиц есть только сопротивле­ние их трению, пропорциональное внешнему давлению; сопротивле­ние же агрегатов частиц с водно-коллоидными связями складывает­ся как из вязкого сопротивления скольжению, величина которого зависит от скорости нарастания сдвигающих усилий, так и сил сцеп­ления, которые в свою очередь зависят от величины уплотняющих давлений, возникающих в точках и на площадках контактов частиц.

Показатели сопротивления сдвигу — эти основные прочностные показатели сопротивления тел внешним силам — для грунтов име­ют ту основную особенность, что они переменны, зависят от давле­ния и условий в точках контакта частиц, сопротивляющихся сдви­жению.

Правильный выбор показателей сопротивления сдвигу грунтов имеет первостепенное значение для практики, так как он обусловли­вает точность инженерных расчетов по определению предельной на­грузки на грунт, устойчи­вости массивов грунта и давления грунтов на ог­раждения.

Опытное определение сопротивления грунтов сдвигу может произво­диться различными мето­дами: по результатам пря­мого плоскостного среза, простого одноосного сжа­тия, трехосного сжатия, среза по цилиндрической поверхности, вдавливания и др.

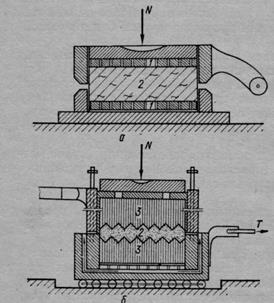
Рис. 17. Срезыватель для испытания грун­тов на сдвиг:

а — при неподвижной нижней части; б — при не­подвижной верхней части; /—фильтры; 2— об­разец грунта; 3 — фильтрующие камни

Предельное сопротив­ление грунтов сдвигу при прямом плоскостном сре­зе определяется при ис­пытании грунтов на одно-срезных приборах (рис. 17); при этом цилиндри­ческий образец грунта (после предварительного уплотнения или без уплот­нения— в зависимости от условий испытания) по­мещается в срезыватель так, чтобы одна его половина оставалась неподвижной, а другая могла перемещаться горизонтально под действием прикладываемой к ней горизонтальной сдвигающей нагрузки, причем должна быть обеспечена возможность увеличения или уменьшения объема грун­та при срезе.

К образцу грунта прикладывается нормальная к поверхности среза сжимающая нагрузка N.

Для лучшей связи штампа с грунтом в штампе устраивают вы­ступы (треугольные или пластинчатые), которые, врезаясь в верх­нюю и нижнюю поверхности образца грунта, обеспечивают связь штампа с грунтом и более равномерное распределение сдвигающих напряжений по плоскости среза.

Сдвигающую касательную к поверхности среза нагрузку т прикладывают к срезывателю ступенями или беспрерывно возрастаю­щей (например, с помощью струи воды, дроби и т. п.) до тех пор, пока не произойдет срез и скольжение одной части грунта по дру­гой. Одновременно с приложением нагрузки и во все время испыта­ния производятся замеры вертикальных и горизонтальных дефор­маций грунта, что дает возможность при испытании уплотненных глинистых грунтов вводить «поправку на косой срез»* и по резуль­татам измерений вычертить диаграмму сдвига (рис. 18).

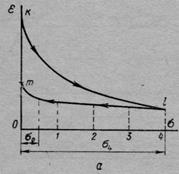
Рис. 18, б иллюстрирует влияние начальной плотности сыпучего грунта на его деформации при сдвиге при постоянной скорости де­формирования. Если же постоянство скорости деформирования не будет выполняться (например, при приложении сдвигающей нагруз­ки ступенями или постепенным ее возрастанием), то вид диаграм­мы сдвига будет такой, как указан на рис. 18, а.

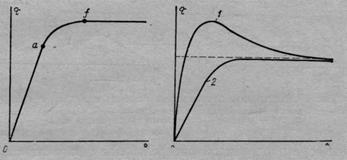
Рис. 18. Диаграммы горизонтальных деформаций грунта при плоскостном сдвиге:

а — при постепенно возрастающей нагрузке; б — при постоянной скорости деформирования; / — для плотного песка; 2— для рыхлого песка; т — сдвигающее напряжение; б — деформация при сдвиге

Следует отметить, что, как показывает диаграмма сдвига (рис. 18, б), сыпучий грунт при сдвиге достигает определенного коэффициента пористости независимо от того, имел ли он вначале плотное или рыхлое состояние. Этот коэффициент получил назва­ние коэффициента критической пористости для данного песчаного грунта при сдвиге, так как пористость плотных грунтов при сдвиге увеличивается, а более рыхлых — уменьшается.

В дальнейшем мы будем рассматривать лишь максимальное (предельное) сопротивление грунтов сдвигу, соответствующее на диаграмме сдвига (рис. 18, а) точке /, когда исчерпывается полно­стью сопротивление грунта сдвигающим усилиям.

Закон Кулона. Сыпучие грунты: различного рода пески (за исключением слюдистых), крупнообломочные грунты, галеч­ники и т. п. при увеличении на них внешнего давления (на величи­ну порядка нескольких кГ/см2) незначительно изменяют свою плотность, и практически этими изменениями при испытании сыпучих грунтов на предельное сопротивление сдвигу можно пренебречь.

После нагружения образца грунта некоторой сжимающей (вер­тикальной) нагрузкой прикладывают сдвигающую (горизонталь­ную) нагрузку, увеличивая ее до тех пор, пока не возникнут без дальнейшего увеличения сдвигающей нагрузки незатухающие, про­грессивно возрастающие деформации сдвига б (рис. 19, а) и произойдет срез (скольжение) одной части образца грунта по дру­гой. Величину максимального предельного сопротивления сдвигу при данной ступени нагрузки относят к единице площади поперечного сечения образца, принимая распределение сдвигающих напряже­ний равномерным. Затем идентичный

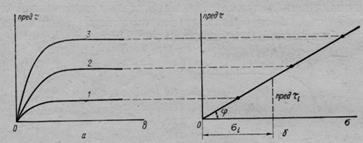
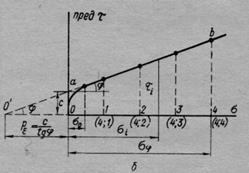
Рис. 19. Диаграмма сопротивлений сдвигу сыпучих грунтов:

а—диаграмма перемещений при сдвиге (/—3 — при различном давле­нии); б— диаграмма предельных сопротивлений сдвигу

образец того же грунта на­гружают большим давлением и вновь определяют максимальное сопротивление сдвигу (срезу). Опыт повторяют при нескольких уплотняющих давлениях о', а", о"' и по результатам их строят диаг­рамму предельного сопротивления сдвигу, откладывая по одной оси (вертикальной) предельное сдвигающее напряжение (пред х кГ/см2), а по другой (горизонтальной)—соответствующее уплотняющее давление (сжимающее напряжение о — рис. 19,6).

Как показывают результаты многочисленных испытаний, диаг­рамма предельных сопротивлений сдвигу для сыпучих грунтов пред­ставляет собой строго прямую, исходящую из начала координат (для идеально сыпучих грунтов) и наклоненную под углом ф к оси давлений (рис. 19, б).

Согласно диаграмме сдвига для сыпучих грунтов любое предель­ное сдвигающее напряжение Тг равно

пред г, = сч 1§ ф (11.18)

или, обозначив коэффициент пропорциональности

1ВФ = /. ИМИ

получим

пред г, = /а*. (11.18')

Так как сопротивление сыпучих грунтов сдвигу есть сопро­тивление их трению, то угол <р носит название угла внут­реннего трения, а величина / = т-&ф—коэффициента внутреннего трения.

Соотношение (11.18) является основной прочностной зависимо­стью для сыпучих грунтов, установленной еще в 1773 г. К. Куло­ном, и может быть сформулировано следующим образом: предель­ное сопротивление сыпучих грунтов сдвигу есть сопротивление тре­нию, прямо пропорциональное нормальному давлению. Эта зависи­мость в механике грунтов носит название закона Кулона.

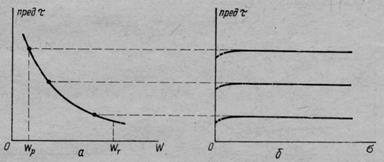
Рис. 20. Диаграмма предельных сопротивлений сдвигу связных гли­нистых грунтов в условиях закрытой системы (неконсолидированно-недренированных):

а — зависимость сопротивления сдвигу от влажности; б— диаграмма сдвига при быстром (недренированном) срезе

Связные грунты (глины, суглинки и супеси) отличаются от грунтов несвязных (сыпучих) тем, что частицы и агрегаты частиц этих грунтов связаны между собой пластичными (водно-коллоид­ными), и частично жесткими цементационно-кристаллизационными связями, при этом сопротивление их сдвигу будет в высокой степе­ни зависеть от их связности (от сил сцепления).

Как было показано в § 2, всякое внешнее давление на водона-сыщенные связные глинистые грунты при условии свободного отто­ка выжимаемой внешним давлением воды вызывает значительное изменение их плотности-влажности, что и сказывается на их общем сопротивлении сдвигу.

Основными видами испытаний связных грунтов на сдвиг будут испытания по закрытой системе (неконсолидированно-недрениро-ванные) и испытания по открытой системе (консолидированно-дре-нированные).

В первом случае образцы связных грунтов должны быть испыта­ны при отсутствии условий выдавливания воды из пор грунта и так, чтобы во время испытания практически не изменялась их плотность-влажность, что можно выполнить лишь при быстром сдвиге. Резуль­таты такого испытания приведены на рис. 20, причем на рис. 20, а дана зависимость сопротивления сдвигу связного (глинистого) грун­та от его влажности или плотности, так как между влажностью и коэффициентом пористости существует для полностью водонасыщенных грунтов прямая зависимость, определяемая формулой (1.7), а на рис. 20, б — от величины нормального уплотняющего давления (сжимающего напряжения а).

Если первая кривая показывает весьма существенное влияние плотности-влажности грунта на его сопротивление сдвигу, то вторая (рис. 20, б) констатирует тот факт, что при недренированном испы­тании и сохранении влажности грунта предельное сопротивление сдвигу предо- практически не зависитот величины внешнего давле­ния (сжимающего напряжения а), изменяясь лишь при изменении плотности-влажности грунта.

Рис. 21. Диаграмма предельных сопротивлений сдвигу связных глинистых грунтов в условиях открытой системы (консолидированно-дренированных):

а—кривая уплотнения (к1) и разуплотнения — набухания {1т); б — диаграмма сдвига

Другой характер имеет диаграмма сдвига связных грунтов, испытываемых по открытой (консолидированно-дренпрованной) системе.

Если принять при испытании связного грунта на сдвиг тот же метод, что и при испытании сыпучих грунтов, т. е. вначале уплот­нять образец грунта некоторым давлением, а затем испытывать его на сдвиг при том же давлении, то результаты ряда испытаний нель­зя будет отнести к одному какому-либо состоянию плотности-влаж­ности грунта, так как каждому давлению будет соответствовать своя влажность-плотность, а результаты испытаний будут характе­ризовать сопротивление сдвигу различных по плотности образцов грунта.

Для получения образцов связного грунта одной и той же плот­ности (одного и того же коэффициента пористости) пользуются ветвью разгрузки (набухания) компрессионной кривой (рис. 21, а), согласно которой до некоторого давления ст0 почти для всех связных грунтов изменения коэффициента пористости при разгрузке весьма незначительны. Поэтому заготовляют несколько образцов грунта, предварительно уплотняя их наибольшим давлением до полной ста­билизации осадок, а затем разгружают до меньших давлений (но больших со) и после стабилизации деформаций разуплотнения ис­пытывают при этих давлениях. В последнем случае можно считать, что сопротивление сдвигу нескольких образцов связного грунта, ис­пытываемых при разном давлении, будет соответствовать его плот­ности-влажности при наибольшем давлении.

Отметим, что существует еще второй способ, предложенный ав­тором настоящей книги, для построения диаграммы сдвига связных грунтов по одному их образцу (естественной или нарушенной струк­туры— в зависимости от условий испытания), используя результа­ты независимого определения сил сцепления, что будет изложено несколько ниже.

Как показывают многочисленные испытания, диаграмма консо­лидированного сдвига связных грунтов в довольно большом диапа­зоне давлений, вполне удовлетворяющем строительную практику (от а0~0,5 кГ/см2 до аФ = 5-г-7 кГ/см2), также хорошо описывается уравнением прямой линии.

Если принять обозначения по рис. 21, б, то уравнение прямой, проведенной через экспериментально найденные точки, будет иметь следующий вид:

пред х, = с + 1д фа», (11.20)

а так как {§ф = /, то

ГпредТ4= с + /о;. (11.20')

^----(С^ з

Уравнение (11.20) выражает закон Кулона для связных грунтов, I который может быть сформулирован следующим образом: предель­ное сопротивление связных грунтов сдвигу при завершенной их кон­солидации есть функция первой степени от нормального давления

(сжимающего напряжения). ,

Угловой коэффициент прямой (1§ф=/) по аналогии с сыпучими грунтами носит название коэффициента внутреннего трения, а па­раметр с, не зависящий в явном виде от величины внешнего давле­ния, — сцепления.

Величины / и с следует рассматривать лишь как математические параметры прямолинейной диаграммы сдвига связных грунтов, со­ответствующие определенной их плотности.

Отметим, что для неконсолидированного состояния полностью водонасыщенных связных грунтов, т. е. когда полного уплотнения от данной нагрузки еще не достигнуто, часть сопротивления сдвигу грунта, зависящая от величины нормального давления, будет мень­ше, так как на скелет грунта передается не все внешнее давление, а лишь эффективное а, равное разности между полным давлением (сжимающим напряжением о) и нейтральным и. Тогда сопротивле­ние сдвигу полностью водонасышенного связного грунта при неза­вершенной консолидации будет по величине промежуточным между сопротивлением сдвигу, соответствующем начальной влажности грунта, и величиной, соответствующей стабилизированному его со­стоянию, и определяется выражением

пред.т = с + 1(а—и), (11.21)

или

пред х = с + \а, (11.21')

где и— нейтральное (поровое) давление, соответствующее данной степени консолидации; с — величина эффективного сцепления.

Величина отрезка с, отсекаемая диаграммой сдвига на оси пре­дельных сдвигов предТ, равна суммарной силе сцепления грунта, соответствующей его плотности-влажности.

Как предложено проф. Н. Н. Масловым («Прикладная механика грунтов», 1949), суммарную величину сцепления с следует рассмат­ривать состоящей из двух слагаемых, что может быть записано (в наших обозначениях) следующим выражением:

с = сс + си,, (11.22)

где сс — структурное жесткое сцепление (обусловленное проч­ностью цементационно-кристаллизационных связей), не­обратимое при разрушении; Су; — пластичное сцепление, обусловленное водноколлоидными обратимыми связями.

Отметим, что при постепенном возрастании сдвигающей нагруз­ки разрушение структурных связей (как вязко-пластичных, так и жестких) будет идти одновременно, и для грунта с чисто водно-кол­лоидными связями при небольших значениях (меньших Оп) началь­ного параметра сопротивления сдвигу с может и не наблюдаться, так как эти связи начинают деформироваться уже при незначитель­ной величине давления. Для некоторых же связных грунтов (напри­мер, илов) может наблюдаться и независимость их сопротивления сдвигу от величины внешнего давления в начале загружения, пока структурная прочность не будет преодолена.

Таким образом, начальный участок диаграммы сдвига (рис. 21,6) требует для отдельных видов грунтов специального изучения. Общая же зависимость, описываемая уравнением (11.21), будет справедлива с учетом сделанных замечаний для очень важного диа­пазона давлений (от о0 ДО о>).

Отметим также, что если продлить предельную прямую аЬ до пересечения с осью давлений о (рис. 21, б) до точки О', то из тре­угольника ОО'а величина параметра с будет равна

с = 18ФРе, (П.23)

где рг —некоторое всестороннее давление, которое мы называем «давлением связности», суммарно заменяющее действие всех сил сцепления. Из соотношения (11.23)

Рг = -^- (И.23')

или

ре = с.с^ф. (11.23")

Это значение напряжений на предельной прямой отвечает неко­торой экспериментальной точке М, которая одновременно должна принадлежать и кругу предельных напряжений Мора (рис. 22).

Выражения (11.23') или (11.23") часто используются в задачах теории предельного равновесия грунтов для вычисления величин, заменяющих силы сцепления связных грунтов.

Различные случаи диаграммы предельных напряжений при сдвиге. Закон Кулона, описываемый уравнениями (11.18) и (11.20), можно распространить и на сложное напряженное состояние грун­тов, если рассматривать диаграммы сдвига как прямолинейную огибающую кругов предельных напряжений Мора, что идентично принятию для грунтов известной из курса «Сопротивления материа­лов» теории прочности Мора.

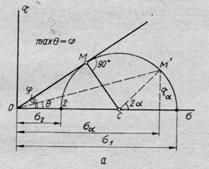
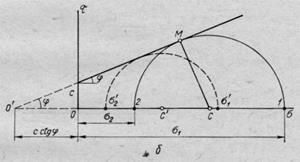
Рис. 22. Диаграмма предельных напряжений при сдвиге грунтов:

а — сыпучих; б — связных

Действительно, величина сдвигающих напряжений не может быть больше их предельного значения, определяемого уравнениями (11.18) или (11.20) и соответствующего возникновению беспрерыв­ного скольжения (сдвига) одной части грунта по другой, т. е.

пред т ^ *{?фа

или

пред т ^ с + 1§ фсг.

Это значение напряжений на предельной прямой отвечает неко­торой экспериментальной точке М, которая одновременно должна принадлежать и кругу предельных напряжений Мора (рис. 22).

Последнее возможно лишь в том случае, когда прямая ОМ (рис. 22, а) или О'М (рис. 22, б) будет касательной к кругу напряжений, т. е. составит с радиусом круга в точке касания угол в 90° и прой­дет через начало координат (О или О').

Изложенное условие может быть записано и в аналитической форме.

Зная величину главных напряжений — наибольшего оч и наи­меньшего Ог (определяя их, например, по кругу напряжений как абсциссу пересечения круга с осью о, если круг напряжений постро­ен по известным для некоторой площадки, наклоненной под углом а к оси давлений, значениям ха и аа, или непосредственно по резуль­татам соответствующих испытаний) и учитывая, что в диаграмме сдвига (см. рис. 22) треугольник ОМС или О'МС прямоугольный, будем иметь:

по рис. 22, а (для сыпучих грунтов)

СМ

а так как

<х1 — 02 „ „ , 04— 02 01 + 02

СМ =--_ и ОС = 02 +-— =---,

то

01—02 ,,.„..

81Пф = --; (11.24)

01 + 02

по рис. 22, б (для связных грунтов)

01 — 02

СМ 2

5*П* = -СГС = — 7 а.^ + 02

СС^ф + 02 Н----

или

01 — 02 т ос\

51Пф = -■-. (П.2о)

01 + 02+2сс1§ф

Уравнения (11.24) и (11.25) являются математической формули­ровкой условия предельного равновесия (условия прочности) сыпу­чих (11.24) и связных (11.25) грунтов. Это условие имеет огромное число практических приложений и используется при определении предельной нагрузки на грунт, расчетах устойчивости массивов грунта и давления грунтов на ограждения.

Отметим также, что показатели сопротивления грунтов сдвигу (с кГ/см2 и / = г§ф) являются лишь математическими параметрами прямолинейной огибающей кругов предельных напряжений. Одна­ко, как показывают детальные исследования, если рассматривать предельные (разрушающие) сопротивления грунтов сдвигу в большом диапазоне изменения уплотняющих давлений и различных на­пряженных состояниях (простых и сложных), огибающая кругов предельных напряжений в общем случае будет криволинейной (рис. 23). При не очень же больших изменениях давлений (при а<сГф = 5-г-7 кГ/см2) часть огибающей кривой предельных напря­жений (отрезок аЬ на рис. 23) можно с полным к тому основанием принимать прямолинейным, т. е. до давлений, меньших о~ф, будет полностью справедлив закон Кулона и следующие из него условия предельного напряженного состояния грунтов [уравнения (11.24), (11.25)].

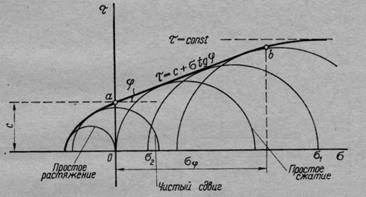
Рис. 23. Общий случай огибающей предельных (разрушающих) напряжений при сдвиге (по результатам испытаний при про­стых и сложных напряженных состояниях)