В статье описаны основные принципы проектирования релейных схем в соответствии с заданным алгоритмом их работы.

В двух предыдущих статьях было рассказано об основах булевой алгебры и алгебры релейных схем. На этой основе были разработаны структурные формулы, а уже по ним типовые контактные схемы.

Составить структурную формулу по готовой схеме — дело несложное. Значительно труднее по готовой структурной формуле представить электрическую схему будущего автомата. Здесь нужна определенная тренировка!

На рисунке 1 показаны наиболее часто встречающиеся варианты контактных схем и их эквиваленты. Они помогут при составлении электрических схем автоматов, а также анализировать уже готовые конструкции, например в процессе их ремонта.

Как же можно использовать разобранные выше варианты контактных схем?

Рассмотрим схему, приведенную на рисунке 2, а. Соответствующая ей структурная формула имеет вид: (A + B)*(С + D).

Пользуясь распределительным законом алгебры Буля, раскроем скобки в этом выражении и получим: A*(С+D) + B*(С +D), что соответствует схеме, изображенной на рисунке 2, б. Далее, за счет перемножения, можем получить формулу A*C + A*D + B*C + B*D, соответствующую рисунку 2, в.

Все три схемы эквивалентны, то есть оказываются замкнутыми при одних и тех же условиях. Однако, по сложности они разные.

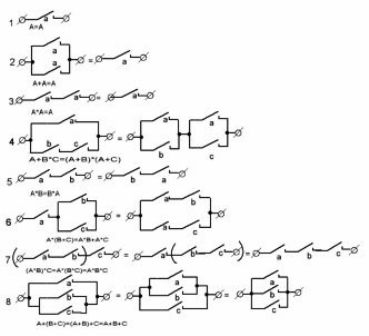
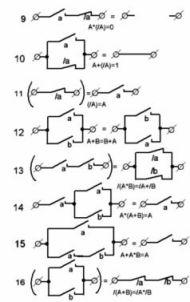
Рисунок 1. Типовые контактные схемы

Первая из схем, самая простая, она требует четырех реле, каждое из которых должно иметь по одному нормально разомкнутому контакту. (Для упрощения рисунков катушки реле не показаны).

Схема «б» требует реле с двумя контактными группами. Собственно, основной задачей алгебры контактных схем является отыскание всех эквивалентных схем с тем, чтобы можно было выбрать из них наиболее простую.

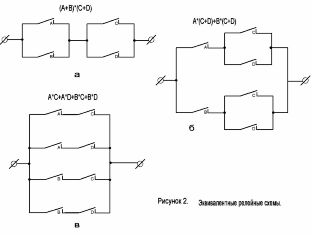
Рисунок 2. Эквивалентные контактные схемы.

Для закрепления пройденного материала попробуйте самостоятельно решить следующие задачи.

1. Начертите электрическую схему автомата, имеющего структурную формулу A*B*C*D + A*B*E + A*D.

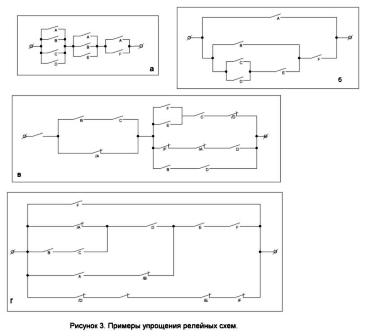
2. Докажите, что схемы, приведенные на рисунке 3, а и б, эквивалентны.

3. Упростите схему, показанную на рисунке 3, в.

4. Какой структурной формулой реализуется схема на рисунке 3, г?

После того, что мы уже успели изучить, можно будет приступить к решению задач, которые были заданы в самом начале первой статьи. Вкратце их напомним.

Первая задача была о включении и выключении лампочки в комнате тремя переключателями, расположенными в разных местах: у двери, у стола, у кровати.

Вторая задача о голосовании спортивных судей: из четырех судей «ЗА» должны проголосовать хотя бы двое, при том условии, что «ЗА» проголосовал председатель комиссии.

Третья задача была просто для учебных целей. В ней предлагалось то же, что и в первой, только для шести переключателей, как будто в комнате шесть стен. Подобные схемы как раз разрабатываются при помощи алгебры релейных схем.

Вообще, если мы хотим разработать схему, обладающую некоторыми заданными логическими свойствами, то к решению подобной задачи можно подойти двумя разными путями. Условно эти пути могут быть названы «интуитивным» и «алгебраическим».

Некоторые задачи лучше решаются первым путем, а другие вторым. Интуитивный подход оказывается удобнее в случае, когда работа схемы управляется многими переключателями, но имеется какая-то симметрия во взаимном расположении этих реле. Мы увидим, что здесь интуитивный подход быстрее приводит к цели, тогда как применение аппарата релейной алгебры в случае многих переменных может оказаться очень громоздким. Полезно познакомиться с обоими возможными подходами к решению указанной задачи.

Начнем с интуитивного подхода. Пусть нам потребовалось построить схему, которая замкнута тогда, когда сработали все n управляющих схемой реле.

Решение этой задачи не требует длительных размышлений: ясно, что поставленное условие будет выполнено, если соединить между собой последовательно n нормально разомкнутых контактов реле.

Точно так же очевидно, что для построения схемы, которая замыкает тогда, когда сработало, по крайней мере, одно из n реле, достаточно соединить n нормально разомкнутых контактов реле параллельно.

Легко представить себе такую схему, которая замыкается тогда, когда срабатывают некоторые, но не все реле. Такая схема изображена на рисунке 4, а. Справа приведена схема, действующая по принципу «все или ничего». Она будет замкнута только тогда, когда сработают все реле или реле отключены (рисунок 4, 6).

Рассмотрим теперь более сложный пример. Пусть имеется n контактов, расположенных в некоторой определенной последовательности: A, В, С, D, E, F… Построим схему, которая замыкается тогда, когда замкнуты какие либо k последовательно включенных контактов, и только они. Такая схема для значений n = 7 и k = 3 изображена на рисунке 4, в. Метод построения таких схем для любых других значений n и k понятен из этого рисунка.

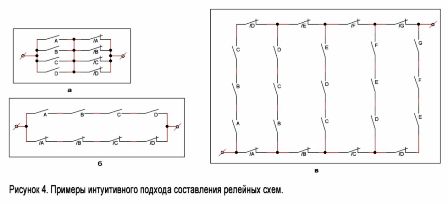
Перейдем к построению схем по данным условиям их работы с помощью релейной алгебры.

Как и прежде, условия работы схемы сначала всегда задаются словесно. Конструктор, прежде всего, должен уметь выразить словами то, что хочет. Если такой ясности у него нет, то никакая алгебра не поможет. Начинать нужно всегда с четкой формулировки требований, которые ставятся перед новой схемой. Как и в любом деле, эта задача, пожалуй, самая сложная. Если условия достаточно просты, то мы можем сразу же написать выражение структурной формулы, удовлетворяющей этим требованиям.

Пример 1. Допустим, что мы должны построить схему, содержащую 4 контакта A, B, C и D так, чтобы цепь была включена тогда, когда замкнуты контакт A, и какой-нибудь из остальных трех контактов. В этом простом случае работа схемы в словесной записи будет выглядеть так: «Схема должна проводить ток, если замкнуты контакты A и B, или контакты A и C или контакты A и D. Согласитесь, что теперь составить структурную формулу очень просто. Она будет выглядеть так:

A*B + A*C + A*D = 1 или A* (B+C+D) = 1.

У схемы два варианта. Они показаны на рисунке 5. Второй вариант не требует реле с тремя нормально разомкнутыми контактами.

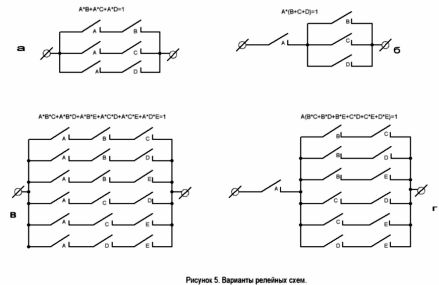
Пример 2. В первой статье была задача №2 о голосовании спортивных судей. Прочтите ее условие повнимательней, оно схоже с только что разобранным примером. Более четкая словесная запись требований будет выглядеть так: «Необходимо составить схему, содержащую 5 контактов A, B, C, D, E, так, чтобы она проводила ток и включала лампочку табло, если замкнуты следующие контакты:

A и B и C, или A и B и D, или A и B и E, или A и C и D, или A и C и E, или A и D и E. Контакт A — это кнопка председателя. Если она не нажата, то каждое из 6 логических произведений будет равно 0, т.е. голосование не состоялось.

Структурная формула будет такой:

(A*B*C)+(A*B*D)+(A*B*E)+(A*C*D)+(A*C*E)+(A*D*E) = 1,

или A*(B*C + B*D + B*E + C*D + C*E + D*E) = 1.

Оба варианта схемы изображены на рисунке 5, в и г. Это и есть решение поставленной задачи.

Имея некоторый навык в чтении структурных формул, легко представить схему самого автомата и все его возможности. Интересно то, что алгебра релейных схем дает больше информации, чем даже сама схема. Она позволяет видеть, сколько и каких требуется реле. С ее помощью легко можно найти самый простой вариант схемы автомата.

ПРИМЕР 3. Получив некоторый опыт в составлении структурных формул, попробуем решить задачу, с которой начиналась первая статья: вам нужно сконструировать переключатель, позволяющий включать свет при входе в подъезд и выключать после того, как вы поднялись на нужный этаж, или, наоборот, включать при выходе из квартиры и выключать после того, как спуститесь вниз. Та же самая ситуация случается в длинном коридоре: в одном конце лампочку надо зажечь, а пройдя до другого конца, погасить. Одним словом, задача сводится к управлению одной лампочкой из разных мест двумя переключателями.

Выберем следующий порядок решения задачи: сначала четко сформулируем условия работы переключателей, затем запишем их в виде формулы, и уже по ним начертим электрическую схему.

Итак, чтобы лампочка горела (1), нужно, чтобы было выполнено одно из двух условий:

1. Включить переключатель внизу (А) и выключить наверху (/В). Входите в подъезд.

2. Включить переключатель наверху (В) и выключить внизу (/А) Выходите из квартиры.

С использованием принятых обозначений структурная формула запишется так:

А*(/В)+(/А)*В = 1

Схема переключателя показана на рисунке 6. В настоящее время такие переключатели выпускаются промышленно, это так называемые проходные переключатели. Поэтому рассмотрение данных схем здесь приводится просто для понятия общих принципов их работы.

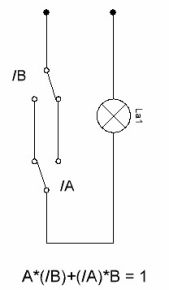
Рисунок 6.

В задаче №1 в начале первой статьи речь шла о схеме, позволяющей включать и выключать свет в комнате любым из трех переключателей. Рассуждая точно так же, как в случае двух переключателей получаем структурную формулу:

А*В*(/С)+А*(/В)+(/А)*В*С = 1.

Схема, составленная по этой формуле, представлена на рисунке 7.

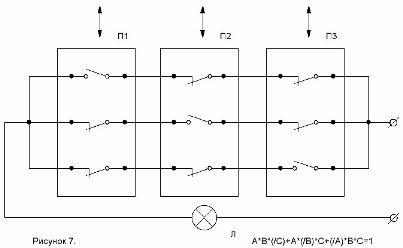
Рисунок 7.

В начале первой статьи была предложена просто учебная задача №2: как будто в комнате шесть стен, и на каждой по переключателю. Логика работы схемы точно такая же, как и для трех переключателей. Обозначим их буквами A, B, C, D, E, F. Напомним, что обозначение (/А), (/В) и так далее, это не знак деления, а логическое отрицание. Чаще обозначается подчеркиванием символов и, даже целых выражений, сверху. В некоторых схемах это подчеркивание заменяется просто знаком «минус». Итак, структурная формула для шести переключателей имеет вид:

(/A)*B*C*D*E*F+A*(/B)*C*D*E*F+A*B*(/C)*D*E*F+A*B*C*

(/D)*E*F+A*B*C*D*(/E)*F+ A*B*C*D*E*(/F) = 1.

Полную электрическую схему, реализующую данную структурную формулу, читателям предлагается составить самостоятельно для приобретения практических навыков проектирования схем. Небольшая подсказка: для схемы понадобится шесть реле, каждое из которых имеет по одному нормально – разомкнутому контакту и по пять нормально замкнутых. Подобные сложные реле при необходимости можно собрать из нескольких более простых, соединив их катушки параллельно.

На этом мы заканчиваем рассказ о булевой алгебре и алгебре релейных схем.

Логические микросхемы. Часть 1