Логическое умножение (операция "И").

В элементарной алгебре А*А =А2. Но в алгебре Буля А*А = А2 = А, А * А = А так как знак умножения (*) теперь обозначает...И... в смысле И...И. Весь наш опыт подтверждает, что и А И А — это то же самое, что одно А. С этим нельзя не согласиться. Истинность высказывания не меняется, если его повторить сомножителем несколько раз.

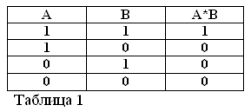
Произведение двух высказываний считается истинным (равным 1), тогда, и только тогда, когда оба сомножителя истинны, и ложным (равным 0), если хоть один из сомножителей ложен. Согласитесь, что эти правила не противоречат здравому смыслу, и, кроме того, они полностью соответствуют правилам элементарной алгебры:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Первое равенство читается так: если и А и В истинны, то произведение А*В истинно. В алгебре Буля знак умножения (*) заменяет союз И.

Логические произведения могут включать не два, а большее число высказываний — сомножителей. И в этом случае произведение бывает истинным только тогда, когда одновременно истинны все высказывания-сомножители.

Логическое сложение (операция "ИЛИ")

Если два высказывания соединить союзом ИЛИ. то образованное сложное высказывание называется логической суммой.

Рассмотрим пример логической суммы. Высказывание А: «Сегодня я пойду в кино».

Высказывание В: «Сегодня я пойду на дискотеку». Складываем оба высказывания и получаем: «Сегодня я пойду в кино ИЛИ на дискотеку».

Это сложное высказывание обозначается так: А + В = С или (А V В) = С.

Через С мы обозначили сложное высказывание логической суммы.

В рассматриваемом примере союз ИЛИ нельзя употреблять в исключающем смысле. Ведь в один и тот же день можно попасть И в кино И на дискотеку. А вот высказывание:

«Председателем садового товарищества будет Петров или Иванов»—не является логической суммой, потому, что председателем будет только кто-то один, а другой простым рядовым садоводом - любителем.

Знак V для обозначения логической суммы выбран потому, что это начальная буква латинского слова «vel», обозначающего «или», в отличие от латинского слова «aut>, обозначающего «и». Теперь всем должно быть ясно, почему логическое произведение обозначается знаком ^.

В элементарной алгебре есть правило A + А = 2А. Это правило верно, какое бы число ни изображалось буквой А. В булевой алгебре ему соответствует правило А + А = А. Весь наш жизненный опыт говорит, что сказать А ИЛИ А ИЛИ оба А есть лишь другой и более длинный способ сказать просто А.

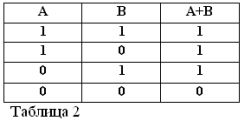
Как и всякое сложное высказывание, сумма двух высказываний А и В может быть истинной или ложной. Сумма считается истинной, то есть равной единице, если хоть одно из слагаемых истинно:

А + В = 1, если ИЛИ А = 1 ИЛИ В = 1, что согласуется с обычной арифметикой:

1+0 = 0+1 = 1.

Если оба складываемых высказывания истинны, то сумма считается также истинной, поэтому в алгебре Буля имеем: (1) + (1) = 1.

Скобки здесь поставлены для того, чтобы подчеркнуть условный, смысл этого сложения, а не арифметический.

Сумма двух высказываний считается ложной и равной нулю тогда, а только тогда, когда оба слагаемых ложны. Отсюда:

0 + 0=0.

Итак, сумма двух высказываний А + В считается истинной, если истинно ИЛИ А, ИЛИ В, ИЛИ оба слагаемых вместе. Таким образом, слово ИЛИ обозначается знаком +.

Помня, что высказывания А и В могут быть только истинными или ложными и, следовательно, иметь меру истинности 1 или 0, результаты рассмотренных операций И и ИЛИ можно свести в таблицы 1 и 2.

Третья операция, широко используемая алгеброй Буля, — операция отрицания — НЕ. Напоминаем, элементарная алгебра пользуется операциями СЛОЖИТЬ, ВЫЧЕСТЬ, УМНОЖИТЬ НА, РАЗДЕЛИТЬ НА и некоторыми другими.

Для каждого высказывания А существует его отрицание НЕ А, которое мы будем обозначать символом /А. Это ни у кого не должно вызывать сомнения.

Приведем примеры: «Мы поедем в лес» А, «Мы не поедем в лес» /А.

Если высказывание А истинно, то есть А = 1, то его отрицание /А обязательно должно быть ложно /А = 0. И наоборот, если какое-либо высказывание ложно, то его отрицание истинно. Например: «Лошадь не ест сена» /А = 0, «Лошадь ест сено» (А = 1). Это можно выразить таблицей 3.

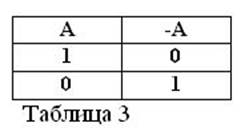
Определяя смысл действия отрицания, и полагая, что из двух высказываний А и /А всегда одно истинно, следуют две новые формулы алгебры Буля:

А + (/А) = 1 и А* (/А) = 0.

Имеются еще и другие формулы, упрощающие логическую обработку высказываний. Например, 1+А = 1, так как, согласно определению сложения, в случае, когда одно слагаемое равно единице, сумма всегда равна единице. Полученный результат не зависит от того, будет ли А = 0 или А = 1.

Каждая из трех рассмотренных нами логических операций (И, ИЛИ, НЕ) обладает определенными свойствами, близкими к правилам элементарной алгебры. Если все их сформулировать, то получим 25 правил булевой алгебры. Их вполне достаточно для решения почти любой логической задачи. Без этих правил решать логические задачи из-за их кажущейся запутанности становится довольно трудно. Пытаться найти правильный ответ, не пользуясь правилами, — значит заменять их смекалкой и общими рассуждениями. Правила значительно облегчают эту работу и экономят время.

В рамках статьи невозможно рассмотреть все эти 25 правил, но желающие всегда могут найти их в соответствующей литературе.

Как уже упоминалось в первой статье в 1938 году молодой американский ученый Клод Шеннон в статье «Символический анализ релейных и переключательных схем» впервые использует булеву алгебру для задач релейной техники. Открытие Шеннона состояло в том, что он понял, что метод конструирования релейных автоматов и электронных вычислительных машин представляет собой фактически раздел математической логики.

Так часто бывает. Ученый долгие годы трудится над какой-либо проблемой, которая его соотечественникам кажется совершенно ненужной — просто забавой. Но проходят десятилетия, а иногда и века, и никому не нужная теория не только приобретает право на существование, но без нее уже становится немыслим дальнейший прогресс.

Что помогло Шеннону вторично «открыть» булеву алгебру? Случай? Ничего подобного.

Любовь к релейным автоматам, построенным на обычных выключателях и реле, помогли молодому ученому связать забытую теорию с задачами автоматических телефонных станций, над которыми он работал в то время. В дальнейшем ту же идею «да или нет» Шеннон ввел в рассмотрение дискретных сообщений и заложил основу целого раздела кибернетики—теории информации.

Алгебра Буля очень подошла для анализа и синтеза релейных схем. Достаточно было в качестве истинного высказывания принять: «Сигнал в цепи есть», а в качестве ложного — «Сигнала в цепи нет», как появилась новая алгебра — алгебра сигналов, алгебра релейных схем.

Новая алгебра справедлива только для рассмотрения релейных и переключательных цепей. Ведь только в таких схемах удовлетворяется условие «сигнал есть» и «сигнала нет». Там, где сигнал меняется непрерывно, приобретая сколь угодно большое число промежуточных условий (такой сигнал называется аналоговым), релейная алгебра неприменима. Об этом нужно всегда помнить. Но как раз большинство электронных вычислительных машин и кибернетических автоматов используют дискретный принцип обработки сигналов, в основу которого положены элементы «да — нет».

Выражение «Контакт замкнут» Шеннон принял за истинное (1), а «Контакт разомкнут» — за ложное (0). Всю остальную «алгебру», включая операции И, ИЛИ и НЕ и 25 правил Шеннон заимствовал у Буля.

Алгебра релейных схем получилась проще алгебры Буля, так как она имеет дело только с элементами типа «да — нет». Кроме того, новая алгебра более наглядна.

Элементами в этой алгебре являются контакты, которые мы будем обозначать буквами А, В, С... Контакт замкнут— А, контакт разомкнут — /А (буква с черточкой).

Система обозначений, как видите, полностью взята из алгебры Буля. Разомкнутый контакт является отрицанием замкнутого контакта. Один и тот же контакт не может быть одновременно замкнутым и разомкнутым.

Условимся, что если в какой-либо схеме два контакта обозначены одной и той же буквой, то это значит, что они всегда принимают одни и те же значения.

В каждый данный момент они или оба одновременно разомкнуты, или оба замкнуты. Проще всего их представить механически соединенными вместе так, что оба они одновременно размыкаются или замыкаются.

Если в некоторой цепи какой-либо контакт есть отрицание другого контакта, то их значения всегда противоположны. Например, контакты С и /С никогда не могут быть одновременно разомкнуты или одновременно замкнуты. А на схеме их можно представлять механически соединенными: если один из них размыкается, то другой замыкается.

Знакомство с релейной алгеброй начнем с разбора простейших схем, соответствующих операциям И, ИЛИ и НЕ.

Произведением двух контактов (операция И) будем называть схему, полученную в результате их последовательного соединения: она замкнута (равна 1) только тогда, когда оба контакта замкнуты (равны 1).

Суммой двух контактов (операция ИЛИ) будем называть схему, образованную при их параллельном соединении: она замкнута (равна 1) тогда, когда замкнут (равен 1) хотя бы один из образующих схему контактов.

Противоположный данному контакту (операция НЕ)—это контакт, равный 0 (разомкнутый), если данный контакт равен 1 (замкнут), и наоборот.

Как и в алгебре Буля, если контакты обозначены буквами А и В, то произведение двух контактов мы будем обозначать через А*В, сумму — через А + В, а контакт, противоположный А, — через /А. Сказанное поясним рисунками 1, 2 и 3.

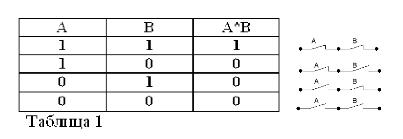
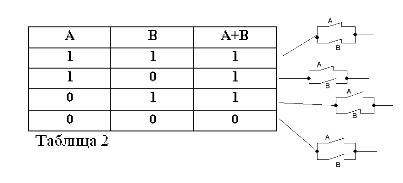
Достоверность таблиц, соответствующих операциям И, ИЛИ и НЕ. теперь ни у кого не должна вызывать сомнений.

Остановимся на двух примерах: 1*0 = 0 и 1+0=1.

Из рисунка видно, что постоянно замкнутый контакт, последовательно соединенный с постоянно разомкнутым контактом, эквивалентен постоянно разомкнутому контакту (1*0 = 0) Постоянно замкнутый контакт, параллельно соединенный с постоянно разомкнутым контактом, эквивалентен постоянно замкнутому контакту.

Познакомившись с арифметикой контактных схем, можете любую релейную схему описать формулой, используя для этого принятые условные обозначения. В кибернетике такие формулы называются структурными.

Если структурная формула какой-либо релейной схемы равна 1, то через нее сможет пройти сигнал — цепь замкнута. И наоборот, если структурная формула схемы равна 0, сигнал через нее не пройдет — цепь разорвана. Вывод: две релейные схемы эквивалентны друг другу тогда, когда равны их структурные формулы.

В продолжении статьи мы с вами рассмотрим примеры контактных схем, типовые контактные схемы и их эквиваленты, в также составление схем по структурным формулам. Также рассмотрим основные логические микросхемы, выполняющие функции булевой алгебры.

Борис, специально для сайта http://electrik.info/

Булева алгебра. Часть 3. Контактные схемы