Краткие сведения из теории вероятностей и математической статистики

Под случайной величиной X понимается величина, которая в результате измерения (опыта) со случайным исходом принимает то или иное значение из некоторого интервала.

Плотностью распределения непрерывной случайной величины Х называется функция, описывающая вероятность распределения случайной величины на числовой прямой.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений.

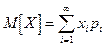
Перейдем от дискретной случайной величины Х к непрерывной с плотностью f(x).

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной величины:

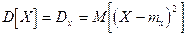
Для непосредственного вычисления дисперсии непрерывной случайной величины служит формула:

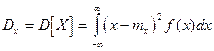
В качестве меры рассеяния также используется среднеквадратическое отклонение величины

.

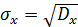Под случайной выборкой объема n понимают совокупность случайных величин, не зависимых между собой.

Упорядоченной статистической совокупностью будем называть случайную выборку, величины в которой расположены в порядке возрастания.

Группированным статистическим рядом называются интервалы с соответствующими им частотами, на которые разбивается упорядоченная выборка, причем ширина интервала находится, как

,

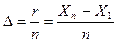где r – размах выборки.

Тогда частоту попадания величины в отрезок 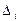находим по формуле

,

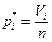где V_i - число величин попавших в отрезок 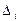, причем 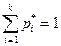. Поделив каждую частоту на 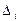, получим высоту для построения гистограммы.

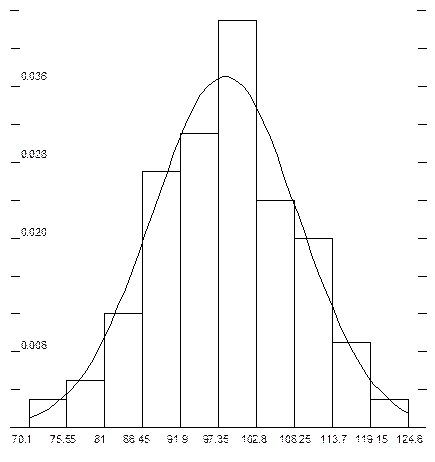
Рис. 1 Пример гистограммы и графика плотности распределения

случайной величины.

Построив гистограмму, мы получили аналог кривой распределения, по которой можем выдвинуть гипотезу о законе распределения. Для выравнивания статистического распределения с помощью закона, о котором выдвинули гипотезу, нужно статистическое среднее (оценка математического ожидания) m_x^* и статистическая дисперсия (оценка дисперсии) D_x^*.

Находим их как

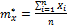
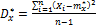
Плотность распределения случайной величины характеризует закон распределения случайной величины. Существуют различные законы распределения: равномерный закон распределения (закон равномерной плотности), закон Пуассона, нормальный закон, закон Эрланга и т.д.

Наиболее часто встречающийся на практике закон распределения - нормальный. Плотность распределения описывается формулой

.

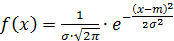Вероятность попадания случайной величины в интервал от a до b определяется зависимостью

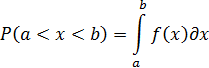
или, используя т.н. функцию Лапласа ( 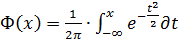), значения которой табулированы,

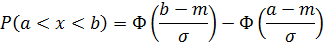
Для нормально распределенной случайной величины все рассеяние с точностью до 1% укладывается в интервале .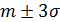

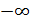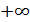Нормальный закон описывает распределение случайной величины на интервале от до . Однако, как правило, интервал распределения случайной величины ограничен конкретными значениями величины a и b. В таком случае используется усеченный нормальный закон распределения , отличающийся множителем – нормирующим коэффициентом, который определяется по зависимости

.

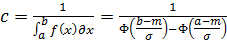Выше рассматривалась вероятность попадания случайной величины X в заданный неслучайный интервал (a,b). Если повернуть ситуацию иначе: величина X не случайна, зато случаен интервал (a,b). Случайно его положение на оси абсцисс, определяемое его центром m, случайна длина интервала. Вероятность того, что случайный интервал (a,b) накроет точку X, называется доверительной вероятностью. А сам интервал – доверительным интервалом. Границы интервала называются доверительными границами.

Дерево исходов

Пусть в результате некоторого эксперимента возможны различные исходы. Будем предполагать, что ни один из исходов w₁, w₂, ... , w_n нельзя представить в виде комбинации остальных (как говорят, w₁, w₂, ... , w_n неразложимы).

Неразложимые исходы w₁, w₂, ... , w_n некоторого эксперимента будем называть элементарными событиями, а их совокупность

W={w₁, w₂, ... , w_n} (конечным) пространством элементарных событий или пространством исходов.

Обычно интересуются не тем, какой конкретно исход имеет место в результате испытания, а тем, принадлежит ли исход тому или иному подмножеству всех исходов. Все те подмножества А, для которых по условиям эксперимента возможен ответ одного из двух типов: «исход w Î A» или «исход w Ï A», будем называть событиями.

Вероятностью P(A) события A называется число, равное отношению числа |A| элементарных исходов, составляющих A, к числу |W| всех элементарных и равновозможных исходов.