Количественные критерии оценки тесноты связи
| Величина коэффициента корреляции | Характер связи |
До 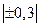
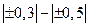
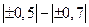
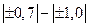
| Практически отсутствует Слабая Умеренная Сильная |
Значимость линейного коэффициента корреляции проверяется на основе 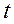 - критерия Стьюдента:
- критерия Стьюдента:
при 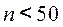
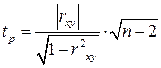 ;
;
при 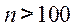
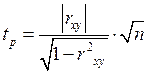 .
.
При этом выдвигается и проверяется гипотеза ( 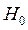 ) о равенстве коэффициента корреляции нулю
) о равенстве коэффициента корреляции нулю 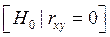 . при выполнении
. при выполнении 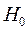
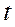 -статистика имеет распределение Стьюдента с входными параметрами:
-статистика имеет распределение Стьюдента с входными параметрами: 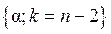 . Если расчетное значение
. Если расчетное значение 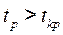 (табличное), то гипотеза
(табличное), то гипотеза 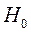 отвергается, что свидетельствует значимости линейного коэффициента корреляции, а, следовательно, существенности зависимости между
отвергается, что свидетельствует значимости линейного коэффициента корреляции, а, следовательно, существенности зависимости между 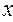 и
и 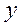 .
.
Таблица 8.3
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |
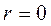
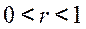
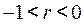
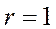
| Отсутствует Прямая Обратная Функциональная | -
С увеличением 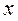 увеличивается увеличивается 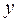 С увеличением
С увеличением 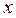 уменьшается уменьшается 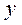 Каждому значению факторного признака строго соответствует одно значение результативного признака
Каждому значению факторного признака строго соответствует одно значение результативного признака
|
Коэффициенты ассоциации ( 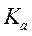 ) и контингенции (
) и контингенции ( 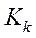 ) определяют тесноту связи двух качественных признаков, каждый из которых состоит только из двух групп.
) определяют тесноту связи двух качественных признаков, каждый из которых состоит только из двух групп.
Таблица 8.4
Таблица для вычисления коэффициентов ассоциации и контингенции
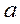
| 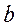
| 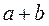
|
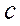
| 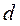
| 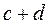
|
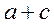
| 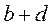
| 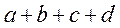
|
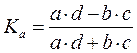 ;
; 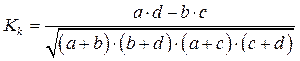 .
.
Коэффициент контингенции всегда меньше коэффициента ассоциации; связь считается подтвержденной, если 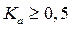 или
или 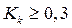 .
.
Коэффициент взаимной сопряженности Пирсона-Чупрова ( 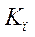 и
и 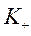 ) определяет тесноту связи более чем двух качественных признаков, каждый из которых состоит более чем из двух групп.
) определяет тесноту связи более чем двух качественных признаков, каждый из которых состоит более чем из двух групп.
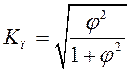 и
и 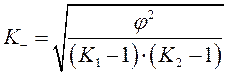 ,
,
где 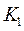 - число значений (групп) первого признака;
- число значений (групп) первого признака;
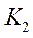 - число значений (групп) второго признака;
- число значений (групп) второго признака;
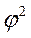 - показатель взаимной сопряженности, причем
- показатель взаимной сопряженности, причем
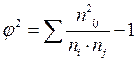 .
.
Таблица 8.5
Вспомогательная таблица для расчета коэффициента
Дата добавления: 2016-05-25; просмотров: 615;
