Географические и прямоугольные координаты

Географические координаты. Земля имеет форму сфероида, т. е. сплюснутого шара. Так как земной сфероид весьма мало отличается от шара, то обычно этот сфероид называют земным шаром.

Земля вращается вокруг воображаемой оси и делает полный оборот за 24 ч. Концы воображаемой оси называются полюсами; один из них называется северным, а другой — южным.

Мысленно разрежем земной шар плоскостью, проходящей через ось вращения Земли. Эта воображаемая плоскость называется плоскостью меридиана. Линия пересечения этой плоскости с земной поверхностью называется географическим или истинным меридианом. Меридианов можно провести сколько угодно, и все они пересекутся в полюсах.

Плоскость, перпендикулярная земной оси и проходящая через центр земного шара, называется плоскостью экватора, а линия пересечения этой плоскости с земной поверхностью называется экватором.

Если мысленно пересечь земной шар плоскостями, параллельными экватору, то на поверхности Земли получатся круги, которые называются параллелями.

Нанесенные на глобусы и карты параллели и меридианы составляют градусную сетку (рис. 63). Градусная сетка дает возможность определить положение любой точки на земной поверхности.

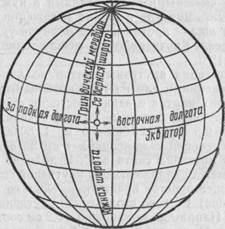
Рис. 63.Градусная сетка

За начальный меридиан при составлении карт в метрических мерах принят Гринвичский меридиан, проходящий через Гринвичскую обсерваторию (вблизи Лондона).

Положение любой точки на земной поверхности, например точки А (рис. 64), может быть определено следующим образом: определяется угол ф между плоскостью экватора и отвесной линией из точки А (отвесной линией называется линия, по которой падают тела, не имеющие опоры).

Этот угол ф называется географической широтой точки А.

Широты отсчитываются по дуге меридиана от экватора к северу и к югу от 0 до 90°. В Северном полушарии широты положительны, в Южном — отрицательны.

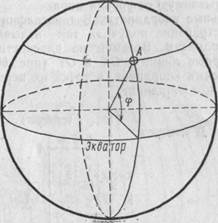
Рис. 64.Определение широты точки А

Угол К, заключенный между плоскостями начального меридиана и меридиана, проходящего через точку А, называется географической долготой точки Л (рис. 65).

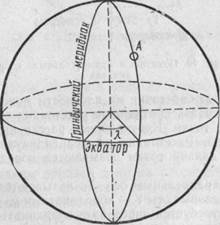
Рис. 65. Определение долготы точки А

Долготы отсчитываются по дуге экватора или параллели в обе стороны от начального меридиана от 0 до 180°, на восток со знаком «плюс», на запад — со знаком «минус».

Географические широта и долгота точки называются ее географическими координатами.

Чтобы полностью определить положение точки на земной поверхности, необходимо знать еще третью ее координату — высоту, отсчитываемую от уровня моря.

Прямоугольные координаты. В топографии наиболее широкое распространение получили так называемые прямоугольные координаты. Возьмем на плоскости две взаимно перпендикулярные линии — ОХ и ОУ (рис. 66). Эти линии называются осями координат, а точка их пересечения О называется началом координат.

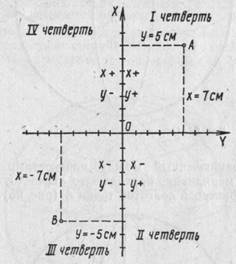
Рис. 66. Понятие о прямоугольных координатах

Положение любой точки на плоскости можно легко определить, если указать кратчайшие расстояния от осей координат до данной точки. Кратчайшими расстояниями являются перпендикуляры. Расстояния по перпендикулярам от осей координат до данной точки называются координатами этой точки.

Отрезки, параллельные оси X, называются координатами х, а параллельные оси У — координатами у.

Например, требуется определить координаты точек А и В. Из рис. 66 видно, что точка А имеет координаты: х = 7 см, = 5 см, а точка В: х= - 7 см, у = —5 см.

Система прямоугольных координат. Прямоугольные координаты, о которых шла речь, применяются на плоскости. Отсюда они получили название плоских прямоугольных координат. Эта система координат с успехом применяется на небольших участках местности, принимаемых за плоскость.

Для того чтобы применить систему плоских прямоугольных координат к сферической поверхности земного шара, приходится допускать некоторые условности.

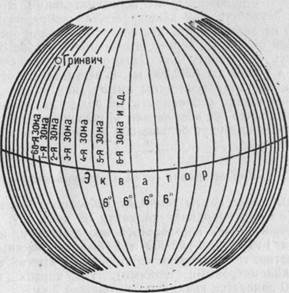
Рис. 67. Шестидесятиградусная зона

Так как развернуть шар на плоскости без разрывов невозможно, весь земной шар условно делят линиями земных меридианов на 60 зон (рис. 67).

Для того чтобы получить зону на плоскости, ее проектируют на цилиндр, а затем этот цилиндр развертывают.

Строго говоря, зона, спроектированная на цилиндр, будет несколько искажена, в особенности на краях, но это искажение настолько незначительно, что практически его можно не принимать во внимание.

Получив таким образом зону на плоскости, к ней можно применить систему плоских прямоугольных координат. Осью X является средний (осевой) меридиан зоны, а осью У — экватор. Пересечение осевого меридиана с экватором называется началом координат. Каждая зона имеет свое начало координат. Счет зон ведется от Гринвичского меридиана, который является западным для 1-й зоны.

Эта система координат называется системой прямоугольных координат.

Счет координат х ведется в метрах от экватора к полюсам. К северу от экватора все х положительны (имеют знак «плюс»), к югу отрицательны (имеют знак «минус»). Очевидно, что на всем протяжении СССР, а также Европы и материка Азии координаты х положительны.

Счет координат у ведется от осевого меридиана. К востоку от осевого меридиана координаты у имеют знак «плюс», к западу— знак «минус». Вся территория СССР занимает 29 зон (с 4-й по 33-ю включительно), и в каждой зоне встречаются координаты у положительные и отрицательные. Это связано с рядом неудобств, так как, записывая координаты, всякий раз надо не забыть поставить соответствующий знак. Чтобы избавиться от знаков, вернее, чтобы иметь только один знак, условились координату для осевого меридиана считать не за нуль, а за 500 км (500 000 м). В результате этого координаты у в пределах всей зоны имеют знак «плюс», который при записи можно отбрасывать, не опасаясь путаницы.

Очевидно, что все координаты у, идущие на восток от осевого меридиана, будут больше 500 км, а идущие на запад — меньше 500 км.

6. Километровая сетка и пользование ею

Каждый лист карты занимает небольшую часть зоны, а поэтому начало координат на карту не попадает. Для того чтобы можно было пользоваться координатами, на картах масштаба 1:10000, 1:25000 и 1:50000 нанесены координатные сетки, т. е. квадраты со стороной 1 км (их также называют километровыми сетками). На картах масштаба 1 : 100 000 наносятся квадраты со стороной 2 км.

Вертикальные линии сетки параллельны осевому меридиану, а горизонтальные — экватору. Счет горизонтальных километровых линий ведется снизу вверх, а вертикальных — слева направо.

Наклон сетки объясняется тем, что западная и восточная линии рамки, представляющие собой географические меридианы, не параллельны осевому меридиану и образуют с ним некоторый угол, называемый сближением меридиан. Но так как все вертикальные линии координатной сетки параллельны осевому меридиану, то и вся сетка будет наклонена по отношению к вертикальным линиям рамки на такой же угол.

Пользование координатной сеткой рассмотрим на примере.

Требуется определить по карте координаты тригонометрического пункта на высоте 141,5 (рис. 68).

Сначала нужно определить расстояние в метрах от экватора до данной точки. Это будет координата х; координатой у этой точки будет расстояние в метрах от осевого меридиана (считая осевой меридиан за 500000 м). Целые километры определяют по цифрам за рамкой, а доли километра (метры) измеряют внутри квадрата в масштабе карты, таким образом, координаты тригонометрического пункта будут х = 5 880 700, у = 5 297 300.

При практической работе в пределах одного или двух листов карты для сокращения записи первые две цифры отбрасываются, так как они повторяются.

Рис. 68. Координатная сетка на карте

Следовательно, координаты тригонометрического пункта будут х = 80 700, у = 97 300.

Определять координаты точек по карте и, наоборот, наносить на карту точки по координатам приходится при указании целей и всего местоположения, привязке к точкам карты огневых позиций и наблюдательных пунктов, ориентировании на карте, постановке задач, докладах и донесениях.

Чтобы определить и указать по карте сокращенные координаты какой-нибудь точки (например, определить координатами положение цели или своей точки стояния), надо назвать квадрат, в котором расположена эта точка. Квадрат всегда указывается координатами его юго-западного угла (нижнего левого угла). Для того чтобы узнать эти координаты, надо прочитать за рамкой карты цифровые обозначения километровых линий, образующих этот угол. При этом необходимо соблюдать следующее правило: прежде читать цифры, относящиеся к горизонтальной линии (у правой или левой рамки карты), т. е. координату х, а затем — относящиеся к вертикальной линии (у верхней или нижней рамки), т. е. координату у. Эти отсчеты, состоящие всегда из четырех цифр, называются сокращенными координатами. Они записываются и читаются без разделения их на х и у, например сокращенные координаты моста (рис. 69) будут 1552 (читается «пятнадцать пятьдесят два, мост»). Иначе говоря, сокращенные координаты какой-либо точки — это номер квадрата карты, в котором находится данная точка.

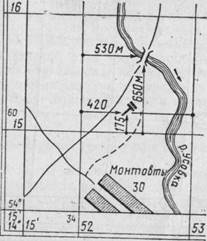
Рис. 69. Определение координат точки

Если положение точки в пределах квадрата требуется указать более точно, измеряют в метрах на карте по масштабу сначала расстояние (по перпендикуляру) от заданной точки до ближайшей снизу горизонтальной километровой линии, а затем так же измеряют расстояние до ближайшей слева вертикальной линии. Полученные отсчеты прибавляют к сокращенным координатам х и у. При этом полученные уточненные кординаты х и у записывают и передают (по телефону, радио) раздельно. Например, уточненные координаты перекрестка указанных выше дорог будут х=15650 м, у— = 52 530м.

Нередко приходится решать обратную задачу. Допустим, что цель (пулемет противника) расположена на местности в точке, ничем не отмеченной по карте, но известны ее уточненные координаты. Например, х=15175 м, у = 52420 м. Требуется нанести эту цель на карту.

Задачу решают так (см. рис. 69):

определяют квадрат, в котором расположена цель (ее сокращенные координаты); для этого отделяют у координат х и у по две первые цифры — в нашем примере 15 (горизонтальная километровая линия) и 52 (вертикальная линия);

в квадрате 1552 откладывают по масштабу вверх по вертикальным линиям сетки 175 м и полученные точки соединяют прямой линией; на ней должна находиться цель;

откладывают по прочерченной линии 420 м вправо от вертикальной линии сетки (52); полученная точка и будет местом расположения цели.