Окно и видовой экран
Термин окно (window) в сетевой компьютерной среде обозначает область экрана монитора, посредством которого пользователь взаимодействует с вычислительными ресурсами, подключенными к той же сети. В компьютерной графике этот термин имеет иное значение. Окно — это область пространства, проецируемая на монитор. Объекты, находящиеся вне окна, на мониторе не появляются. В этом смысле оно подобно окну дома, через которое человеку, сидящему внутри дома, видна лишь часть внешнего мира. Вероятно, эта аналогия была основанием для выбора соответствующего термина. Окно обычно определяется как прямоугольник, лежащий на экране и заданный значениями Хv и Yv в системе координат просмотра. Видимая область пространства, называемая просматриваемым объемом (viewing volume), зависит от типа проекции. Для параллельной проекции эта область имеет форму параллелепипеда, а для перспективной — форму пирамиды (рис. 3.9 и рис. 3.10).
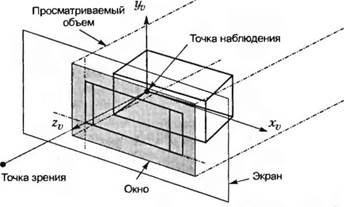
Рисунок 3.9 - Окно и просматриваемый объем для параллельной проекции
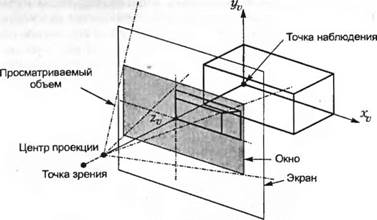
Рисунок 3.10 - Окно и просматриваемый объем для перспективной проекции
Просматриваемый объем при проецировании может давать довольно сложное изображение, поскольку в него могут попадать ненужные объекты, расположенные вблизи наблюдателя или вдали от него. Иногда бывает удобно ограничить этот объем двумя плоскостями, из которых одна располагается ближе, а другая - дальше (рис. 3.11). Для параллельной проекции ближняя и дальняя плоскости определяются так же, как и для перспективной.

Рисунок 3.11 - Ближняя и дальняя плоскости
Видовой экран (viewport) — это область экрана, где будет отображаться проецируемое изображение (рис. 3.12).
В эту область проецируется просматриваемый объем, определяемый «обычным» окном. Отображение состоит из трансляции и масштабирования, учитывающих расстояние между центром видового экрана и центром монитора, а также разницу размеров окна и видового экрана. Другими словами, значения Xs и Ys, полученные по формулам (3.1) и (3.2), должны быть увеличены или уменьшены таким образом, чтобы центр окна попадал в центр видового экрана, а не в центр монитора.

Рисунок 3.12 - Видовые экраны
Кроме того, они должны быть подвергнуты масштабированию, чтобы четыре граничные точки окна стали четырьмя граничными точками видового экрана. Соотношение сторон у окна должно быть таким же, как и у видового экрана, в противном случае изображение будет искажено, и круг, например, превратится в эллипс.
Примитивы
Примитивы (primitives) — это элементы графики, которые могут отображаться графической библиотекой. В каждой библиотеке набор примитивов свой, поэтому в данном разделе мы рассмотрим только наиболее общие примитивы, поддерживаемые большинством графических библиотек.
Отрезок
Для отображения отрезка прямой (линии — line) необходимо задание координат двух его концов. В большинстве графических библиотек координаты концов могут задаваться в трехмерном пространстве; проецирование на плоскость экрана осуществляется автоматически. Можно указывать атрибуты отрезка: тип, толщину, цвет и другие. Типы отрезков, поддерживаемых большинством графических библиотек, изображены на рис. 3.13. Для систем автоматизированной разработки чертежей поддержка этих типов линий совершенно необходима, поскольку они часто используются в машиностроительных и архитектурных чертежах и электрических схемах.

Рисунок 3.13 - Различные виды отрезков
В библиотеках GKS, PHIGS и OpenGL одной из базовых функций является ломаная (polyline), представляющая собой набор соединенных друг с другом отрезков. Координаты концов отрезков, составляющих ломаную, задаются в виде матрицы. В случае ломаной, состоящей всего из одного отрезка, в матрицу помещаются координаты двух его концов.
Многоугольник
Многоугольник — это то же самое, что и ломаная, за небольшим исключением: первая и последняя строки матрицы вершин должны быть одинаковыми (соответствующие им точки совпадают). Того же результата можно было бы достичь и с использованием функции построения ломаной, однако многоугольник, построенный при помощи специальной функции, распознается системой как объект, имеющий внутреннюю и внешнюю части. Внутренняя площадь многоугольника может быть заполнена штриховкой различных видов (рис. 3.14).
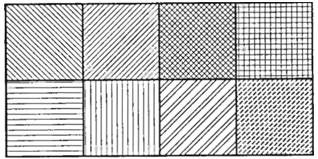
Рисунок 3.14 - Примеры различных штриховок
Атрибутами многоугольника могут быть цвет внутренней области (цвет заполнения), а также тип, ширина и цвет ломаной, ограничивающей эту область. Хотя функция построения многоугольников может использоваться и для построения кругов и прямоугольников, в большинстве графических библиотек существуют специальные функции, требующие гораздо меньше входных параметров (например, центр и радиус круга или два конца диагонали прямоугольника). Тем не менее, внутри библиотек эти функции реализованы через функцию построения многоугольников.
Маркер
Маркеры обычно используются для выделения точек на графиках. Маркеры, доступные в большинстве графических библиотек, показаны на рис. 3.15. Тип маркера указывается в качестве атрибута. Полимаркер, как и отрезок, является стандартным объектом в GKS и PHIGS. OpenGL не поддерживает маркеры явно, однако предоставляет механизм сохранения маркеров в растровых файлах и выведения их на экран. Благодаря этому графическая программа, построенная на OpenGL, гораздо лучше переносится на различные платформы.
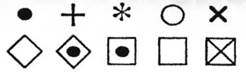
Рисунок 3.15 - Примеры маркеров
Текст
Большинство графических библиотек поддерживают два вида текста: текст для пояснений (экранный или двумерный текст) и трехмерный текст. Текст для пояснений всегда располагается в плоскости экрана, поэтому его форма не искажается вне зависимости от угла, на который он повернут. Трехмерный текст может быть расположен на любой плоскости в трехмерном пространстве. Его положение и ориентация задаются в мировых координатах. Для текста любого вида необходимо задание таких параметров, как шрифт, отношение высоты к ширине и угол наклона букв, а также положение и направление строки текста. Текст может быть представлен символами двух видов: аппаратными и программными. Программный шрифт строится соответствующими графическими программами, заранее сохраняемыми в памяти компьютера. Построение его занимает больше времени, чем построение символов аппаратного шрифта, но зато форма может быть гораздо более замысловатой. Символы аппаратного шрифта состоят из отдельных отрезков, формирующих буквы.
Ввод графики
Как уже отмечалось, графической программе может требоваться поддержка ввода графических элементов, таких как точки, отрезки и многоугольники, а не только чисел и текстовых строк. Например, если пользователь хочет вычислить площадь многоугольника на экране или увеличить его размеры, он должен сначала указать интересующий его многоугольник среди прочих объектов, видимых на экране. Для ввода графики используется два вида физических устройств: локатор (устройство ввода координат) и кнопка. Локатор (locator) передает графической программе информацию о своем положении, то есть о положении курсора. Кнопка (button) сообщает о действиях пользователя (включении и выключении) в месте текущего положения курсора. В наши дни наиболее популярным устройством графического ввода является мышь, которая выполняет обе функции. Шарик в нижней части корпуса мыши позволяет вводить координаты, а кнопки наверху корпуса передают программе действия пользователя.
Устройство графического ввода может работать в трех режимах: опрос, запрос и выбор. В режиме опроса (sampling) осуществляется постоянное считывание состояния устройства ввода, прежде всего положения локатора. Например, если вы свободно рисуете на экране, перемещая мышь, она работает в режиме опроса. Перемещение мыши приводит к непрерывному перемещению курсора по экрану. В режиме запроса (requesting) положение локатора считывается только при отправке запроса, который обычно производится при нажатии на кнопку мыши. Чтобы прояснить различие между режимами опроса и запроса, рассмотрим процесс построения многоугольника путем графического задания координат его вершин при помощи мыши. В этом случае мы перемещаем мышь до тех пор, пока курсор не окажется в нужном месте, после чего нажимаем кнопку. Курсор перемещается по экрану согласно движениям мыши, которая находится при этом в режиме опроса. Координаты вершин передаются графической программе в режиме запроса. У этих режимов есть общее свойство: графической программе передаются координаты мыши или курсора. В режиме выбора (picking) устройство графического ввода идентифицирует элемент экрана, на который указывает курсор в момент нажатия кнопки. Графические элементы можно идентифицировать по именам, присвоенным им программистом во время составления программы. Режим выбора очень удобен при редактировании чертежа, уже имеющегося на экране (например, для удаления многоугольников или изменения координат их вершин).
Дисплейный файл
Дисплейный файл (display list) — это группа команд графической библиотеки, сохраненная для последующего выполнения. Большинство команд графических библиотек могут либо помещаться в дисплейный файл, либо выполняться немедленно. Дисплейный файл обеспечивает удобство и эффективность упорядочения и обработки команд библиотеки. Рассмотрим, например, перемещение изображения дома по экрану. Предположим, что рисунок состоит из нескольких сотен отрезков. Если бы эти отрезки существовали по отдельности, нам пришлось бы написать команду перемещения несколько сотен раз — для каждого из них. Однако если команды построения отрезков, образующих рисунок, объединены в дисплейный файл, команду перемещения достаточно написать только один раз. Чтобы поместить графические элементы в дисплейный файл, нужно открыть этот файл перед первой командой, которая должна в него попасть, и закрыть его после последней команды:
OpenGL
glNewList(AREA_FILL. GL_C0MPILE_AND_EXECUTE):
/* Открытие дисплейного файла с именем AREA_FILL. */
g1Begin(GL_P0LYGON):
glVertex2fv(pointl):
glvertex2fv(point2):
..
..
glEnd( ):
/* Определение многоугольника. */
glEndList( ):
/* Закрытие дисплейного файла. */
Дисплейный файл OpenGL ориентирован на оптимизацию производительности, в частности, при работе по сети, но не за счет производительности на отдельном компьютере. Оптимизация обеспечивается благодаря тому, что дисплейный файл хранится в виде списка команд, а не в виде динамической базы данных. Другими словами, созданный дисплейный файл изменить уже нельзя. Если бы его можно было изменять, производительность упала бы из-за накладных расходов на поиск внутри списка и управление памятью. Изменение отдельных частей дисплейного файла потребовало бы перераспределения памяти, что могло бы привести к ее фрагментации. Дисплейные файлы, как правило, работают так же быстро, как и обычные последовательности команд, не объединенные в группы. В случае OpenGL дисплейные файлы могут значительно повысить производительность, в особенности при передаче подпрограмм OpenGL по сети, поскольку файлы эти хранятся на сервере, благодаря чему сокращается сетевой трафик. К созданному дисплейному файлу могут быть применены следующие операции:
□ множественное выполнение (multiple execution) — один и тот же файл можно выполнять много раз;
□ иерархическое выполнение (hierarchical execution) — иерархическим называется дисплейный файл (родительский), вызывающий другие дисплейные файлы (дочерние). Иерархические дисплейные файлы удобны для объектов, состоящих из отдельных компонентов, особенно если некоторые компоненты входят в объект в нескольких экземплярах;
□ удаление (deletion) — дисплейный файл может быть удален.
Матрица преобразования
Как говорилось выше, проецирование точек на объект в трехмерном пространстве требует преобразования координат из одной системы в другую. Сначала нужно перевести координаты точек объекта из модельной системы в мировую. Текущее положение объекта обычно задается через повороты и смещения относительно исходного положения, в котором модельная система координат совпадала с мировой. Следовательно, мировые координаты точек объекта можно получить трансляцией и поворотом соответствующих точек из их исходного положения, в котором их модельные координаты совпадали с мировыми. Большинство графических библиотек выполняют эти преобразования самостоятельно, а программисту остается задать только смещение и поворот для интересующего его объекта. Однако проектировщику все равно нужно знать законы преобразований, чтобы рисовать объекты в нужных местах без проб и ошибок, в особенности если эти объекты перемещаются достаточно сложным образом.
Получив мировые координаты всех точек объекта в его текущем положении, мы должны вычислить координаты этих точек в наблюдательской системе. Перевод координат из одной системы в другую называется отображением (mapping). Отображение между мировой и наблюдательской системами координат обычно также осуществляется графической библиотекой самостоятельно, по заданным программистом координатам точки зрения, точки наблюдения и направлению вектора вертикали (в мировых координатах).
Трансляция (перенос)
При трансляции объекта на величины а,в и с в направлениях x,yи z соответственно по отношению к начальному положению, в котором модельная система координат совпадала с мировой (рис. 3.16), мировые координаты точек объекта в новом положении (Xw, Yw, Zw) вычисляются следующим образом:

Рисунок 3.16 - Трансляция (перенос) объекта
Xw = Xm+а;
Yw= Ym+b; (3.3)
Zw= Zm + с
В этой формуле числа Хт, Ym, Zm являются также модельными координатами точки.
Формула (3.3) может быть записана в матричной форме1:
| XXw | "1 | aa | XXm | ||||
| YYw | = | bb | YYm | ||||
| ZZw | cс | zZm | |||||
| 1 1 | L0 |
 (3.4)
(3.4)
Trans (a, b, c)
Легко убедиться, что формулы (3.4) и (3.3) эквивалентны друг другу: для этого достаточно записать (3.4) в развернутом виде. Операцию сложения в (3.3) удалось написать через умножение в (3.4) благодаря использованию однородных координат, в которых трехмерный вектор записывается через четыре скаляра вместо трех[2]. Матрица, которую мы получили, называется матрицей однородного преобразования (homogeneous transformation matrix). Вданном случае преобразование является трансляцией. Если бы преобразование (в частности, трансляцию) нужно было применить к точке в двумерном пространстве, однородная матрица преобразования редуцировалась бы до матрицы размерностью 3x3 удалением третьей строки и третьего столбца из матрицы размерностью 4x4. Новая матрица действовала бы на вектор координат размерностью 3x1, полученный из вектора 4x1 удалением z - координаты.
Другие матрицы преобразования
Помимо матрицы преобразования трансляции, часто используются матрицы вращения, отображения (в другой системе координат), масштабирования и зеркального отображения, матрицы преобразования для которых выводятся аналогичным образом.
Удаление невидимых линий и поверхностей
Проекция на экран станет более наглядной, если будет содержать только видимые линии и поверхности. Удаление невидимых линий (hidden-line removal) заключается в блокировании отображения отрезков, скрытых от наблюдателя, а удаление невидимых поверхностей (hidden-surface removal) есть то же самое по отношению к поверхностям. Удаление невидимых линий иллюстрируют рис. 3.17. Очевидно, что эта процедура значительно облегчает восприятие объекта.

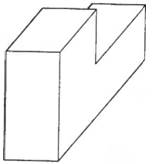
Рисунок 3.17 - Изображение до и после удаления невидимых линий
Опубликовано множество программных алгоритмов удаления невидимых линий и поверхностей. Их авторы пытаются повысить вычислительную эффективность и расширить диапазон объектов для применения своих алгоритмов. Однако лучше всего удаление реализуется посредством графического устройства, которое называется z-буфером, поэтому в настоящее время исследования на эту тему практически не ведутся.
Метод z-буфера
Метод z-буфера основан на том же принципе, что и алгоритм сортировки по глубине: на любом участке экрана оказывается проекция элемента, расположенного ближе всех прочих к наблюдателю. Здесь под элементами понимаются точки, кривые или поверхности. Данный метод требует использования области памяти, называемой z-буфером. В этом буфере для каждого пиксела хранится значение координаты Zv того элемента, проекция которого изображается данным пикселом. Как уже говорилось, значение Zv (то есть координата z в наблюдательской системе) есть мера удаленности объекта от наблюдателя. Объем z-буфера определяется количеством пикселов, для каждого из которых требуется сохранить вещественное число.
Грани, векторы нормали которых направлены от наблюдателя, невидимы для него, поэтому на экран проецируются только те грани, векторы нормали которых направлены к наблюдателю. Однако в отличие от метода сортировки по глубине, в данном случае порядок проецирования значения не имеет. Причина станет очевидной, как только вы прочитаете приведенное ниже описание алгоритма. Сначала проецируется произвольно выбранная поверхность, и в ячейки памяти z-буфера, соответствующие пикселам проекции поверхности, записываются значения координат Zv точек поверхности, являющихся прообразами данных пикселов. Пикселы окрашиваются в цвет первой поверхности. Затем проецируется следующая поверхность, и все неокрашенные пикселы, относящиеся к ее проекции, окрашиваются в цвет второй поверхности. Если пикселы уже были окрашены, соответствующие им значения Zv сравниваются со значениями Zv точек текущей поверхности. Если сохраненное значение Zv какого-то пиксела оказывается больше текущего (то есть точка на предыдущей поверхности ближе к наблюдателю, чем точка на текущей поверхности), цвет пиксела не меняется. В противном случае пиксел окрашивается в цвет текущей поверхности. Изначально z-буфер инициализируется координатами Zv соответствующими дальней плоскости (см. рис. 3.11), поэтому пикселы проекции первой поверхности автоматически окрашиваются в ее цвет. Повторяя эту процедуру для всех имеющихся плоскостей, мы окрасим все пикселы экрана в цвета ближайших поверхностей (рис. 3.18).

Рисунок 3.18 - Основы метода z- буфера
Как следует из предшествующего описания, метод z-буфера предназначен главным образом для удаления скрытых поверхностей. Однако метод z-буфера с небольшими изменениями позволяет реализовать и построение рисунков со скрытыми линиями. Сначала все поверхности проецируются на экран, причем пикселы окрашиваются в цвет фона (на экране ничего не появляется). При этом z-буфер заполняется правильными значениями Zv. Затем на экран проецируются ребра поверхностей. При этом значения Zv ребер сравниваются со значениями Zv ближайших к наблюдателю поверхностей, уже найденными на предыдущем этапе. Окрашиваются только те пикселы, для которых новые значения Zv, больше исходных. Таким образом, участки ребер, скрытые поверхностями, на экране не появляются. Эта процедура дает правильный рисунок без скрытых линий, но некоторые граничные линии могут оказаться слишком тонкими, потому что некоторые пикселы этих линий будут относиться к поверхностям, ограниченным соответствующими ребрами. Эту проблему легко решить, пододвинув весь объект поближе в момент проецирования ребер.
Визуализация
Изображения без невидимых линий и поверхностей в большинстве случаев передают форму объекта достаточно хорошо. Однако для некоторых приложений желательно иметь возможность строить более реалистичные изображения. Особенно важную роль реалистичность играет в «виртуальной реальности» — относительно новой технологии, позволяющей имитировать на компьютере реальные ситуации. Например, вы можете занести в компьютер сведения о внутреннем и внешнем виде проектируемого здания, а затем пройтись по нему и вокруг него, чтобы прочувствовать, как оно будет выглядеть на самом деле. Это средство может оказаться очень полезным для принятия решения о вложении денег в постройку здания.
Для имитации реальной сцены нужно воспроизвести эффекты, создаваемые светом, падающим на поверхности объектов. Этот процесс называется визуализацией или тонированием (rendering). Вообще говоря, все, что мы видим, — это отражение света от поверхностей, а по этому отраженному свету мы определяем форму, текстуру и цвет объекта. В усовершенствованных графических библиотеках обычно имеются некоторые средства визуализации. Для их применения достаточно задать фасетированную модель объекта, условия освещенности и свойства поверхностей (например, блестящие или тусклые). Однако для правильного использования технологий визуализации необходимо иметь представление об их основах. Даже задать правильные значения параметров функций визуализации без достаточно хорошего знания техники визуализации непросто. Поэтому в настоящем разделе мы коротко опишем две основные технологии визуализации: затушевывание (shading) и трассировку лучей (ray tracing). Подробное описание технологий визуализации можно найти в большинстве книг по компьютерной графике.
Затушевывание
Процедура затушевывания аналогична удалению невидимых поверхностей с той разницей, что пикселы одной поверхности окрашиваются разными цветами в соответствии с цветом и интенсивностью отраженного света в точке, проектируемой на этот пиксел. Таким образом, основной задачей становится расчет цвета и интенсивности света, отраженного от какой-либо точки объекта. Начнем с расчета интенсивности.
Поверхность объекта может быть освещена светом, исходящим непосредственно от источников, то есть прямым светом (direct illumination), а также светом, отраженным от других поверхностей, дающим окружающее освещение (ambient illumination). Свет, отраженный данной точкой объекта, получается сложением отраженных лучей двух типов (рис. 3.19).

Рисунок 3.19 - Прямое и окружающее освещение
Отраженный от множества поверхностей сцены свет может считаться приходящим с бесчисленного множества направлений, поэтому отражение окружающего освещения считается равномерно распределенным во всех направлениях. Поэтому интенсивность отражения Ra записывается по формуле:
Ra=KdIa (3.5)
Здесь 1a — интенсивность окружающего освещения, a Kd — коэффициент отражения поверхности. У белых поверхностей коэффициент отражения близок к единице, а у черных — к нулю. Наблюдатель будет воспринимать одну и ту же интенсивность отраженного окружающего освещения вне зависимости от своего положения, поскольку это освещение образуется благодаря отражению от всех поверхностей и распределяется равномерно по всем направлениям.
Для описания прямого освещения достаточно рассмотреть лишь точечные источники света, поскольку линейные и поверхностные источники могут быть рассмотрены как совокупность точечных. Отражение света от точечного источника рассматривается как комбинация двух видов отражения: диффузного и зеркального.
Диффузное отражение (diffuse reflection) состоит в том, что поверхность поглощает свет, а затем переизлучает его равномерно во всех направлениях (рис. 3.20). Интенсивность диффузного отражения (как и отражения окружающего освещения) не зависит от положения наблюдателя. Особенности структуры поверхности, такие как текстура и цвет, становятся видимыми именно благодаря диффузному отражению. Для грубых поверхностей отражение является преимущественно диффузным, а не зеркальным.
Зеркальное отражение (specular reflection) — это прямое отражение света поверхностью. Данный тип отражения характерен для блестящих поверхностей, таких как зеркала. Блестящие поверхности отражают почти весь падающий свет и потому обладают повышенной яркостью (рис. 3.21). Интенсивность зеркального отражения воспринимается по-разному в зависимости от положения наблюдателя относительно сцены.
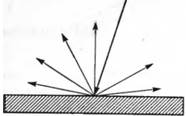
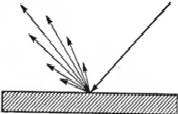
Рисунок3.20 - Диффузное отражение Рисунок3.21 - Зеркальное отражение
Трассировка лучей
Метод затушевывания, описанный в предыдущем разделе, может использоваться в относительно простых условиях, когда один объект освещается далеко расположенными точечными источниками света. Однако он неприменим в случае множества объектов, особенно если некоторые из них прозрачны, а другие преломляют лучи. В сложных ситуациях используется метод трассировки лучей (ray tracing).
Основная идея метода заключается в следующем. Источники света испускают лучи во всех направлениях, и все эти лучи прослеживаются до тех пор, пока они не попадают в одну из точек экрана. В процессе прослеживания вычисляется изменение интенсивности и направления луча при падении его на какой-либо объект. Направление меняется по законам рассеяния, отражения и преломления. Каждая точка экрана (пиксел) окрашивается в цвет, соответствующий интенсивности пучка света в момент его падения на экран. Поскольку для заполнения экрана таким путем пришлось бы проследить бесконечно много лучей, такой подход на практике нереален. Нас интересуют цвета конечного числа пикселов экрана, поэтому рассматривать бесконечное количество лучей не обязательно. Нужно рассмотреть траектории конечного числа лучей в обратном направлении. Луч проходит из центра проекции сквозь каждый пиксел и прослеживается в обратную сторону до тех пор, пока он не выйдет из просматриваемого объема, не упадет на рассеивающую поверхность или не войдет в источник света (рис. 3.22).

Рисунок3.22 - Трассировка лучей
Если луч достиг источника света, это означает, что между источником и экраном отсутствуют непрозрачные препятствия, поэтому пиксел окрашивается в цвет источника. Если луч выходит из просматриваемого объема, значит, никакие объекты на данный пиксел не проецируются, и он должен быть окрашен в цвет фона. Если же луч падает на рассеивающую поверхность, проследить его траекторию дальше невозможно. В этом случае цвет пиксела окрашивается в цвет отражаемого данной поверхностью света. Следовательно, интенсивности света на рассеивающих поверхностях должны быть вычислены заранее по методу затушевывания, описанному в предыдущем разделе.
1)
[1] Silicon Graphics — компания, производившая графические рабочие станции, такие как Indigo и 02.
1Координаты могут быть также представлены в виде строки. Тогда матрица преобразования записывается после вектора координат. В этом случае матрица преобразования представляет собой транспонированную матрицу из формулы (3.4). В формуле (3.4) мы следуем соглашениям о записи OpenGL.
[2] Любой вектор (х, у, z)T трехмерного пространства может быть записан в соответствующих однородных координатах в виде (xw, yw, zw, w)T, где верхний индекс Т обозначает операцию транспонирования. Поскольку значение w может быть произвольным, для каждого вектора существует множество вариантов записи в однородных координатах. В формуле (3.4) используется значение w = 1.
Дата добавления: 2016-05-25; просмотров: 1651;
