Виртуальная и обычная системы координат устройства позволяют задавать положение точки на плоском экране.
Займемся теперь системами координат для работы с трехмерным пространством. Основных трехмерных системкоординат всего три: внешняя система координат (world coordinate system), система координат модели(model coordinate system) и система координат наблюдателя (viewing сoordinate system).
Внешняя, или мировая система координат(world coordinate system), — это опорная система, используемая для описания интересующего нас мира. Внешней она является по отношению к объектам этого мира. Например, такая система может использоваться для описания расположения и ориентации парт, стульев и доски, если интересующий нас мир представляет собой класс.
Следующим шагом является описание формы каждого объекта мира. Форма объекта определяется координатами всех или некоторых характеристических точек объекта по отношению к системе координат, связанной с ним, — системой координат модели (model coordinate system). Координаты точек объекта, определенные таким образом, не изменяются даже тогда, когда объект перемещается или вращается в пространстве. Они действительно зависят только от формы объекта. Система координат модели перемещается вместе с тем объектом, к которому она привязана. Поэтому форма каждого объекта определяется в его собственной системе координат модели. Расположение и ориентация любого объекта задаются относительным положением и ориентацией модельной системы координат данного объекта по отношению к внешней системе координат. Относительное расположение и ориентация систем координат определяются матрицей преобразования, о которой будет рассказано в этой лекции дальше. Наличие внешней системы координат и модельных систем для всех объектов полностью определяет мир, то есть расположение и форму всех объектов данного мира. Другими словами, применение матриц преобразования позволяет получить координаты любой точки любого объекта во внешней системе.
Следующий шаг — проецирование трехмерных объектов или их точек на монитор подобно тому, как они проецируются на сетчатку человеческого глаза. В компьютерной графике используется два вида проекций: перспективная и параллельная (рис. 3.4).
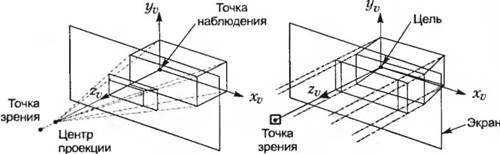
Рисунок 3.4 - Два вида проекций: перспективная и параллельная
Оба вида требуют задания двух точек: точки зрения и точки наблюдения. Точка зрения (viewpoint) — это глаз наблюдателя. Точка наблюдения (viewsite) — это точка объекта, определяющая направление «луча зрения». Вектор, проведенный от точки зрения к цели, задает направление наблюдения.
В перспективной проекции (perspective projection) все точки рассматриваемого объекта соединяются с центром проекции, который обычно лежит на линии, соединяющей точку зрения и цель. Точки пересечения этих линий с экраном образуют проекцию. Экран располагается между точкой зрения и целью. В параллельной проекции (parallel projection) линии от всех точек объекта проводятся в направлении наблюдателя параллельно направлению наблюдения, а точки пересечения этих линий с экраном формируют проекцию.
Экран, как и в перспективной проекции, располагается перпендикулярно направлению проецирования. Такая проекция называется ортогональной. (В косоугольной проекции ориентация экрана произвольна).
Точки проекции, получаемые любым из описанных методов, легко могут быть рассчитаны, если координаты точек проецируемого объекта даны в системе координат xv yv zv (см. рис. 3.4).
(Начало координат наблюдательской системы координат может находиться в точке зрения, а ось zv при этом должна указывать на точку наблюдения. Оси хv и уv определяются так же, как обычно, в результате чего система становится левосторонней. Следствием этого является то, что точки с большими значениями Z оказываются дальше от наблюдателя. По принятому нами соглашению объекты с большими значениями Z расположены ближе к наблюдателю).
Например, координаты точек параллельной проекции объекта попросту равняются соответствующим координатам Xv и Yv точек объекта. Система координат xv yv zv называется наблюдательской(viewing coordinate system), поскольку она облегчает расчет проекции наблюдения. Наблюдательская система координат строится таким образом, чтобы обладать перечисленными ниже характеристиками. Начало этой системы координат располагается в рассматриваемой точке, ось zv направлена из начала координат в точку зрения, а ось уv параллельна вертикальной оси экрана (см. рис. 3.4). Третья ось, хv определяется как векторное произведение первых двух. У большинства людей вертикальное направление в пространстве естественным образом ассоциируется с вертикальным направлением на экране, поэтому ось yv считается проекцией вертикального вектора из пространства на экран. В большинстве графических библиотек пользователю приходится задавать вектор вертикали в пространстве в мировых координатах. Положение точки зрения и точки наблюдения также задается в мировых координатах (рис. 3.5).
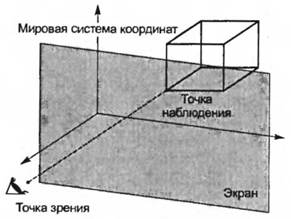
Рисунок 3.5 - Точка зрения и точка наблюдения
После определения наблюдательской системы координат и вычисления координат точек всех интересующих нас объектов остается только вычислить положение их проекций на экране. Мы уже знаем, что для параллельной проекции это сделать очень легко. Поэтому мы займемся описанием процедуры вычисления координат в перспективной проекции. Рассмотрим виды сверху и сбоку (см. рис. 3.4 слева и рис. 3.6). Интересующая нас точка на рисунке выделена, ее координаты мы обозначим как Хv, Уv, Zv.
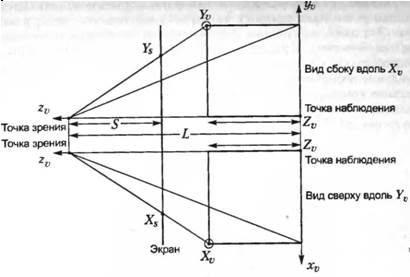
Рисунок 3.6 - Расчет проекции
Из подобия треугольников следует, что
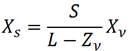 (3.1)
(3.1)
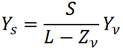 (3.2)
(3.2)
В формулах (3.1) и (3.2) Xs и Ys - расстояния до проекции выбранной точки. Расстояния измеряются в горизонтальном и вертикальном направлениях от точки, где ось Zv пересекается с экраном. Далее, L - расстояние между точкой наблюдения и центром проекции, а S — расстояние между центром проекции и экраном. Формулы (3.1) и (3.2) показывают, что точка с большими значениями Zv, будет иметь большие значения Хs и Ys, благодаря чему далекий отрезок кажется меньше, чем близкий той же длины. Расстояния Xs и Ys преобразуются в виртуальные координаты устройства с учетом желаемого положения центра изображения и его размеров (на мониторе).
Взаимоотношения перечисленных выше систем координат иллюстрирует рис. 3.7.
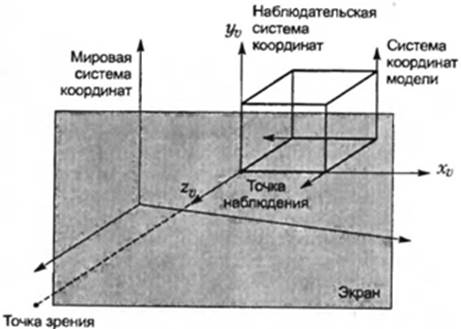
Рисунок 3.7 - Взаимоотношение систем координат
Как уже говорилось, системы координат связаны друг с другом матрицами преобразования. Так, положение и ориентация каждой из модельных систем координат по отношению к мировой задаются соответствующими матрицами преобразований. Наблюдательская система координат также может быть определена относительно мировой при помощи матрицы преобразования, если задать положение точек зрения и наблюдения, а также вектор вертикали. Процедура расчета точек проекции с использованием матриц преобразования выглядит следующим образом. Сначала координаты проецируемой точки преобразуются из модельных в мировые при помощи матрицы преобразования, определяющей переход от модели, к которой относится точка, к мировой системе координат. Эта операция (рис. 3.8) называется преобразованием модели(model transformation). Затем координаты этой точки преобразуются из мировой системы координат в наблюдательскую. Эта операция (см. рис. 3.8) называется преобразованием просмотра (viewing transformation). Наконец, координаты в наблюдательской системе координат преобразуются в значения Xs и Ys по формулам (3.1) и (3.2), а затем — в виртуальные координаты устройства.
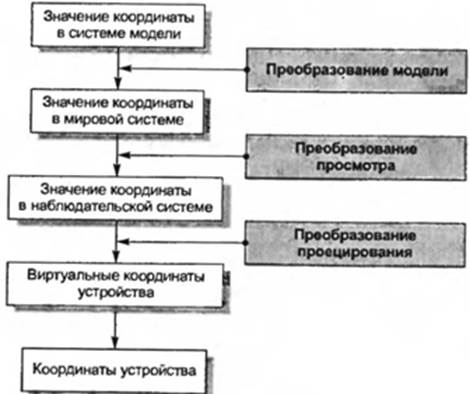
Рисунок 3.8 - Преобразования между системами координат
Эта операция (см. рис. 3.8) называется преобразованием проецирования (projection tranformation). Наконец, виртуальные координаты устройства преобразуются в обычные подпрограммой драйвера.
Все эти преобразования обычно выполняются внутри графической библиотеки, а программисту приходится только указывать сведения, необходимые для проведения преобразований. Например, трансляции и повороты объектов учитываются при преобразовании модели, положение точки зрения, точки наблюдения и вектора вертикали — при преобразовании наблюдения, а тип проекции, расположение центра проекции и экрана — при преобразовании проецирования. Однако графические библиотеки примитивного уровня могут потребовать от программиста самостоятельного написания кода для всех этих преобразований.
Дата добавления: 2016-05-25; просмотров: 2046;
