Теплоемкость твердых тел. Закон Дюлонга и Пти
Определим теплоемкость твердых тел при постоянном объеме СV, имеющих правильную кристаллическую решетку, образованную атомами одного элемента. колебания атомов в узлах решетки можно представить в виде суперпозиции колебаний по трем взаимно перпендикулярным направлениям. Поэтому каждому узлу решетки можно приписать 3 колебательные степени свободы. Как отмечалось выше, на одну колебательную степень свободы при температуре Т приходится в среднем энергия 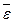 = kT (k — постоянная Больцмана). Очевидно, na атомов одного моля вещества обладают кинетической энергией WK = 3NAkT = 3RT. Обозначим общую потенциальную энергию одного моля атомов твердого тела при их расположении в узлах кристаллической решетки через Un(V). Потенциальная энергия является функцией объема V (средних расстояний между частицами). Полная внутренняя энергия U одного моля вещества определяется кинетической энергией WK колеблющихся в узлах решетки атомов и их потенциальной энергией Un(V):
= kT (k — постоянная Больцмана). Очевидно, na атомов одного моля вещества обладают кинетической энергией WK = 3NAkT = 3RT. Обозначим общую потенциальную энергию одного моля атомов твердого тела при их расположении в узлах кристаллической решетки через Un(V). Потенциальная энергия является функцией объема V (средних расстояний между частицами). Полная внутренняя энергия U одного моля вещества определяется кинетической энергией WK колеблющихся в узлах решетки атомов и их потенциальной энергией Un(V):
U = WK+Uп(V) = 3RT+Un(V). (24.1)
Из (24.1) для молярной теплоемкости СVполучаем выражение
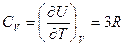 . (24.2)
. (24.2)
Т. е. атомная теплоемкость всех химических простых кристаллических твердых тел оказывается одинаковой и равной 3R. Это утверждение носит название закона Дюлонга и Пти.
Рассмотрим теперь кристалл, образованный сложным химическим соединением, например NaCl. В кристалле соли по узлам решетки располагаются ионы натрия и хлора, их общее число 2NA. Следовательно, молярная теплоемкость двухатомных соединений должна быть CV= 6R, соответственно трехатомных — CV = 9R и т. д.
Если кристалл образован молекулами, имеющими х атомов, то его молярная теплоемкость равна CV = 3xR, т. е. молярная теплоемкость твердых тел равна сумме атомных теплоемкостей элементов, входящих в состав этих тел, — закон Джоуля и Коппа.
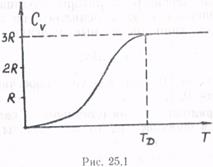
Как показывает эксперимент, закон Дюлонга и Пти (соответственно закон Джоуля и Коппа) выполняется для всех тел выше некоторой температуры TD — температуры Дебая (рис. 25.1), характерной для данного вещества.
Как видно из рис. 25.1, выше температуры TD теплоемкость практически не зависит от температуры.
В табл. 25.1 приведены температуры Дебая для нескольких веществ.
Таблица 24.1
| Вещество | TD, К | Вещество | TD, К |
| Hg Pb К I Na Au KBr Ag NaCl | Zn Ge Al Fe CaF2 FeS3 Si Be С (алмаз) |
С понижением температуры (рис. 25.1) теплоемкость всех тел падает: при стремлении температуры к абсолютному нулю теплоемкость всех твердых тел стремится к нулю. Зависимость теплоемкости от температуры может быть объяснена лишь на основе квантово-механических представлений.
2. Понятие о квантовой теории теплоемкости
Первой попыткой объяснения зависимости теплоемкости твердого тела от температуры была модель Эйнштейна. Согласно этой модели твердое тело представляет собой совокупность атомов, которые колеблются как независящие друг от друга гармонические осцилляторы с одинаковой для всех частотой ν. Энергия ε этих осцилляторов квантуется, т. е. может принимать лишь дискретные значения:
ε = nhv, (24.3)
где h — постоянная Планка; п — квантовое число, принимающее значения л = 0, 1, 2... .
При этом средняя энергия одномерного квантового осциллятора является функцией не только частоты ν, но и температуры тела Т
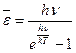 . (24.4)
. (24.4)
В кристалле осциллятор можно считать трехмерным. Поэтому внутренняя энергия одного моля вещества оказывается равной
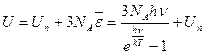 .
.
Продифференцировав это выражение по температуре и умножив числитель на k/k, получим:
 . (24.5)
. (24.5)
При больших Т, разложив в ряд 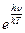 , с достаточной точностью имеем:
, с достаточной точностью имеем:
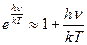 .
.
Поэтому при больших температурах (kT >> hv) теплоемкость не зависит от Т
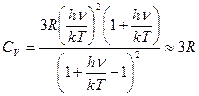 ,
,
т. е. выполняется закон Дюлонга и Пти. При низких температурах
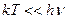 и
и 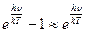 ,
,
поэтому теплоемкость (24.5) убывает по экспоненциальному закону, что противоречит эксперименту.
Дебай несколько изменил модель Эйнштейна: он предложил рассматривать твердое тело как ограниченную размерами кристалла упругую среду, в которой колеблются не только отдельные атомы (с частотами 102—1013 Гц), но и их группы. Очевидно, что коллективные колебания (низкочастотные) выражены тем сильнее, чем ниже температура; наоборот, чем выше температура, тем они слабее; при высоких температурах атомы колеблются независимо. Расчет теплоемкости по Дебаю при низких температурах дал CV ~Т 3, при высоких CV = 3R.
Итак, при низких температурах
CV ~Т 3(24.6)
Соотношение (24.6) — закон кубов Дебая, для многих кристаллов выполняется достаточно хорошо. Отклонения от закона кубов Дебая наблюдается у сложных кристаллов типа графита, у которых CV ~T' 2, и нитевидных, у которых CV ~T.
3. Теплоемкость металлов
До сих пор мы говорили о кристаллах, не разделяя их на диэлектрики и проводники. В металлах на теплоемкость должны влиять свободные электроны: молярная теплоемкость металла С есть сумма теплоемкостей решетки Срш и свободных электронов Сэл:
С = Срш + Сэл. (24.7)
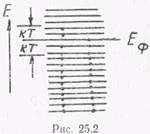 Согласно квантовым представлениям, свободные электроны металла распределяются по дискретным энергетическим уровням, причем на каждом уровне не может быть более двух электронов (рис. 25.2). На рисунке электроны обозначены точками. При абсолютном нуле электроны занимают самые низкие энергетические уровни, наивысший занятый уровень называется уровнем Ферми, а энергия, соответствующая этому уровню, энергией Ферми Еф. Для металлов энергия Ферми порядка 5 эВ. Большая величина энергии Ферми приводит к тому, что число электронов, меняющих свою энергию с увеличением температуры невелико. Действительно, даже для высоких температур величина kT около сотых долей электрон-вольт, поэтому электроны практически не дают вклад в теплоемкость, т. е. Сзл
Согласно квантовым представлениям, свободные электроны металла распределяются по дискретным энергетическим уровням, причем на каждом уровне не может быть более двух электронов (рис. 25.2). На рисунке электроны обозначены точками. При абсолютном нуле электроны занимают самые низкие энергетические уровни, наивысший занятый уровень называется уровнем Ферми, а энергия, соответствующая этому уровню, энергией Ферми Еф. Для металлов энергия Ферми порядка 5 эВ. Большая величина энергии Ферми приводит к тому, что число электронов, меняющих свою энергию с увеличением температуры невелико. Действительно, даже для высоких температур величина kT около сотых долей электрон-вольт, поэтому электроны практически не дают вклад в теплоемкость, т. е. Сзл  0 и
0 и
С = Срш + Сэл 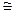 Срш
Срш 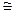 3R. (24.7)
3R. (24.7)
Оценим вклад электронов в теплоемкость на примере одновалентного металла. Если бы в теплоемкость вносили вклад все свободные электроны одного моля, то она была бы равной
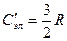 .
.
Однако при температуре Т только часть электронов вблизи уровня Ферми Еф (рис. 25.2) могут изменять свою энергию и, таким образом, вносить вклад в теплоемкость, их доля из общего числа равна 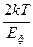 . Поэтому реальная теплоемкость Сэл будет отлична от С'эл:
. Поэтому реальная теплоемкость Сэл будет отлична от С'эл:
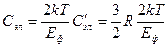 .
.
Свяжем энергию Ферми с температурой Тф, которая должна быть, чтобы электрон имел энергию, равную Еф:
kТф = Еф.
Таким образом, электронная теплоемкость
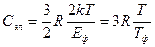 .
.
При Т>Тd отношение 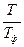 порядка 10-2. Поэтому для металлов коллективизированные электроны практически не влияют на теплоемкость. Электронная теплоемкость, изменяющаяся пропорционально Т, оказывается существенной лишь при низких температурах, так как теплоемкость решетки, пропорциональная Т3, убывает при уменьшении Т вобласти низких температур быстрее, чем электронная. Для большинства металлов решеточная и электронная теплоемкости оказываются одного порядка при температурах около 5 К.
порядка 10-2. Поэтому для металлов коллективизированные электроны практически не влияют на теплоемкость. Электронная теплоемкость, изменяющаяся пропорционально Т, оказывается существенной лишь при низких температурах, так как теплоемкость решетки, пропорциональная Т3, убывает при уменьшении Т вобласти низких температур быстрее, чем электронная. Для большинства металлов решеточная и электронная теплоемкости оказываются одного порядка при температурах около 5 К.
4. Границы применимости классической теории теплоемкости
В заключение оценим температуру TD, выше которой не проявляется квантовый характер теплоемкости, и можно рассчитывать теплоемкость по законам классической физики.
Как уже отмечалось, частицы, находящиеся в узлах кристаллической решетки, совершают колебания около положения равновесия. Вследствие взаимодействия частиц упругой среды друг с другом, колебания передаются от частицы к частице, т. е. распространяются в виде волн (волн малой деформации решетки кристалла) определенных частот v в широком диапазоне от 102 до 1013 Гц. Всякое сложное колебание можно разложить на продольное и два поперечных, плоскости колебаний которых взаимно перпендикулярны. Любое колебание можно представить в виде суперпозиции синусоидальных волн различных частот и амплитуд. Следовательно, в кристалле в результате тепловых колебаний будет распространяться множество продольных и поперечных синусоидальных волн. Волны, дойдя до поверхности кристалла, отражаются и, налагаясь на встречные, образуют систему стоячих волн различных частот.
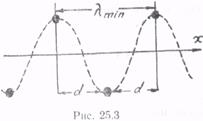 Очевидно, длина волны λ, не может быть меньше чем 2d (d — среднее межатомное расстояние в кристалле). Это легко увидеть из рис. 25.3, на котором изображен мгновенный «срез» поперечной волны, распространяющейся вдоль х (колеблющиеся перпендикулярно оси х атомы изображены точками). Поскольку λmin = 2d, то соответственно максимально возможная частота νmax:
Очевидно, длина волны λ, не может быть меньше чем 2d (d — среднее межатомное расстояние в кристалле). Это легко увидеть из рис. 25.3, на котором изображен мгновенный «срез» поперечной волны, распространяющейся вдоль х (колеблющиеся перпендикулярно оси х атомы изображены точками). Поскольку λmin = 2d, то соответственно максимально возможная частота νmax:
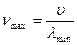
где υ— скорость волны или
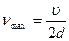 . (24.8)
. (24.8)
Как известно, свет можно рассматривать как волну и как поток частиц фотонов, энергия которых εф пропорциональна частоте ν световой волны εф = hν. Аналогично волне упругой деформации твердого тела, вызванной тепловыми колебаниями частиц в узлах кристаллической решетки, сопоставляют поток квазичастиц-фононов, энергия которых определяется формулой, аналогичной для света,
ε = hv. (24.9)
При таком рассмотрении энергиию колебаний атомов кристалла можно представить как сумму энергий отдельных фононов, а сам кристалл рассматривать как сосуд, наполненный фононным газом.
Основное отличие квазичастиц фононов от «настоящих» состоит в том, что они существуют только внутри кристалла. Фононы не могут существовать в вакууме как фотоны, электроны или другие частицы. Но там, где они существуют, они ведут себя подобно «настоящим» частицам, перенося в кристалле импульс и энергию.
Поэтому будем сопоставлять волне в кристалле с частотой 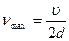 фононы с энергией
фононы с энергией
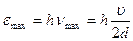 . (24.10)
. (24.10)
С другой стороны, эту же энергию можно выразить через температуру: энергия, приходящаяся на одну колебательную степень свободы при температуре Дебая ТD, соответствующей частоте фононов νmax, равна
ε = kTD. (24.11)
Из формул (24.10) и (24.11) находим TD:
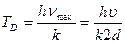 .
.
Оценим порядок величины температуры Дебая. Для кристаллов d≈10-10 м, скорость волн υ ≈ 103 м/с, поэтому
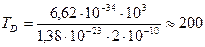 К,
К,
что не противоречит опытным данным.
Теплопроводность
В твердых телах в отличие от газов и жидкостей невозможна конвекция, поэтому перенос тепла осуществляется только за счет теплопроводности.
Если в диэлектрическом кристалле создать разность температуры, то в нем возникнет и установится поток тепла, величина которого определяется формулой
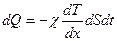 ,
,
где χ— коэффициент теплопроводности; 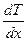 - градиент температуры вдоль направления х; dS — площадь, через которую проходит поток тепла за время dt.
- градиент температуры вдоль направления х; dS — площадь, через которую проходит поток тепла за время dt.
С классической точки зрения теплота передается колебаниями кристаллической решетки. Если атом нагретого участка колеблется с некоторой амплитудой, то, будучи связанным со своими соседями, будет действовать на них, вызывая увеличение амплитуды колебаний соседних атомов. В результате этого процесса энергия тепловых колебаний передается от одной частицы к другой.
По квантовым представлениям тепловое движение решетки заключается в возбуждении фононов, образовании фононного газа. Фононный газ, обеспечивающий процесс теплопроводности в определенном интервале температур, ведет себя подобно идеальному газу, поэтому воспользуемся формулой для коэффициента теплопроводности идеального газа (19.18), применив ее для фононного:
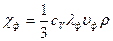 ,
,
где cv— удельная теплоемкость; ρ — плотность вещества; λф — средняя длина свободного пробега фононов; υф— средняя скорость беспорядочного движения фононов.
Средняя длина свободного пробега обуславливается столкновениями фононов друг с другом и их взаимодействием с дефектами решетки. Эти процессы могут привести как к исчезновению фононов, так и рождению новых.
Вычисление средней длины свободного пробега фононов — трудная задача. Согласно теории, при высоких температурах (T > TD)λф обратно пропорциональна температуре. Поэтому для многих веществ при T > TD коэффициент теплопроводности 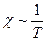 .
.
Анизотропия сил связи в кристаллах приводит к анизотропии коэффициента теплопроводности. Так, для различных направлений в некоторых кристаллах коэффициент теплопроводности отличается в несколько раз.
Как показывает опыт, теплопроводность чистых металлов на два — три порядка превышает теплопроводность диэлектриков. Это объясняется тем, что в металлах основными переносчиками тепла являются валентные электроны, образующие электронный газ, решеточная же теплопроводность составляет 1 — 2% от электронной.
В сильно загрязненных металлах, неупорядоченных сплавах вклад фононов и электронов в теплопроводность примерно одного порядка.
6. Тепловое расширение твердых тел
Изменение размеров тел при нагревании связано с тем, что колебания узлов кристаллической решетки являются ангармоническими. Между частицами, образующими кристаллическую решетку твердых тел, действуют как силы притяжения, так и силы взаимного отталкивания (на существование этих сил указывает способность тел сопротивляться как растяжению, так и сжатию).
На близких расстояниях r < d преобладают силы отталкивания 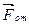 , на более далеких r > d— силы притяжения
, на более далеких r > d— силы притяжения 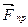 (d — постоянная кристаллической решетки). Сила взаимодействия между двумя соседними частицами определяется результирующей силой
(d — постоянная кристаллической решетки). Сила взаимодействия между двумя соседними частицами определяется результирующей силой 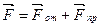 . График зависимости этих сил от r приведен на рис. 25.4, а. Как видно, при некотором расстоянии r = d результирующая сила
. График зависимости этих сил от r приведен на рис. 25.4, а. Как видно, при некотором расстоянии r = d результирующая сила 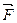 = 0. Расстояние d — такое расстояние между соседними частицами, на котором они находились бы при отсутствии теплового движения. Очевидно, при r = d потенциальная энергия взаимодействия двух соседних частиц минимальна Umin.График зависимости потенциальной энергии от r приведен на рис. 25.4, б.
= 0. Расстояние d — такое расстояние между соседними частицами, на котором они находились бы при отсутствии теплового движения. Очевидно, при r = d потенциальная энергия взаимодействия двух соседних частиц минимальна Umin.График зависимости потенциальной энергии от r приведен на рис. 25.4, б.
При нагревании тела его частицы начинают колебаться около своих положений равновесия. Для низких температур эти колебания можно считать гармоническими относительно d из-за малой величины амплитуды колебаний (на колебаниях практически не сказывается асимметрия потенциальной функции), при повышении температуры они становятся ангармоническими (теперь сказывается асимметрия потенциальной функции взаимодействия).
С изменением в процессе колебаний расстояния r между частицами происходит переход потенциальной энергии частиц U в кинетическую и обратно. Полная энергия при этом остается постоянной (так как силы взаимодействия между частицами являются внутренними и консервативными).
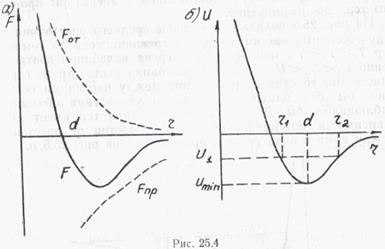
Пусть при температуре тела Т1 расстояние между частицами изменяется от r1до r2 (рис. 25.4,6). При расстояниях r1 и r2их полная энергия равна потенциальной U1(в этих точках кинетическая энергия нулевая). При сближении частиц от r2 до d их потенциальная энергия уменьшается до U min, а кинетическая соответственно возрастает. Это происходит за счет работы, совершаемой результирующей силой, которая притягивает частицы (r >> d, F < 0, рис. 25.4, а). Дальнейшее уменьшение расстояния между частицами сопряжено с совершением работы против результирующей силы, которая теперь отталкивает частицы (r < d, F > 0, рис. 25.4, а). Поэтому кинетическая энергия частиц, достигшая максимума при r = d, будет убывать, а потенциальная — увеличиваться. В момент максимального сближения частиц r = r1) кинетическая энергия равна нулю, а полная равна потенциальной U1. В дальнейшем процесс повторяется в обратном порядке при увеличении r от r1, до d потенциальная энергия уменьшается от U1до Umin, а кинетическая растет за счет силы отталкивания; последующее возрастание r от d до r2 сопровождается уменьшением кинетической энергии и соответствующим ростом потенциальной энергии за счет силы притяжения.
Среднее расстояние между соседними частицами в процессе колебания равно 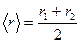 . Оно как правило, больше чем d, поэтому с повышением температуры происходит тепловое расширение.
. Оно как правило, больше чем d, поэтому с повышением температуры происходит тепловое расширение.
На рис. 25.5 показано изменение среднего расстояния между соседними частицами при нагревании тела до температур Т1 < Т2 < Т3, при которых энергия колебаний соответственно U1 < U2 < U3. Если бы колебания были строго гармоническими, то среднее расстояние между частицами оставалось бы без изменений, никакого увеличения объема не наблюдалось бы. Для подавляющего типа тел имеет место зависимость потенциальной энергии частиц от расстояния между ними и вида кривой, приведенной на рис. 25.5, а.
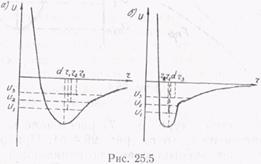
Как видно из графика, с повышением температуры растет среднее расстояние между частицами d < r1 < r2 < r3. Для небольшого количества веществ характерен график на рис. 25.5, б. В этом случае в некотором интервале температур (T1, Т2) r2 < r1 < d, и поэтому наблюдается уменьшение объема (вода, чугун); при более высоких температурах (Т3) объем с повышением температуры растет, как и у всех тел (r3 > d).
В области высоких температур коэффициент среднего линейного расширения α (α — относительное изменение длины, приходящееся на 1°) не зависит от температуры. Для монокристаллов, вследствие анизотропии, по трем взаимно перпендикулярным направлениям значения α1, α2 и α3 могут сильно меняться (в сотни раз). Так, для гипса при комнатной температуре α1 = l,6∙10-6 К-1; α2 = 42∙10-6 К-1; α3 =29∙10-6 К-1.
Изменение температуры по-разному сказывается на величинах α1, α2 и α3. Так, с понижением температуры у некоторых кристаллов наблюдается даже отрицательное значение α, что означает расширение кристалла по осям, где α положителен, и сжатие по тем осям, для которых α отрицателен.
Свяжем изменение объема с изменением линейных размеров. Пусть ребра прямоугольного параллелепипеда, вырезанного из кристалла, при данной температуре 0°С имеют длины L1, L2, L3. При нагревании до температуры t ребра удлинятся и примут значения
L1t = L1(1+ α1t), L2t = L2(1+a2t), L3t = L3 (1+ a3t).
При температуре t объем параллелепипеда равен
Vt=L1L2L3(1+ α1t) (1+a2t) (1+ a3t).
Полагая L1L2L3 = V0 и пренебрегая произведениями α1, α2, α3 и их степенями выше первой, получим
Vt = V0(1+βt),
где
β = α1+ α2 + α3.
Очевидно, для кристаллов кубической формы и поликристаллов, для которых α1= α2 = α3 = α будем иметь
Vt = V0(1+3αt),
т. е. коэффициент объемного расширения β = Зα.
| <== предыдущая лекция | | | следующая лекция ==> |
| Влияние дефектов кристаллов на их прочность | | | рекомбинации, перезарядки |
Дата добавления: 2016-05-25; просмотров: 9037;
