ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ЧАСНЫХ ПРОИЗВОДНЫХ

МЕХАНИЧЕСКИЙ СМЫСЛ ЧАСТНЫХ ПРОИЗВОДНЫХ

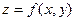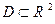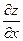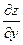Рассмотрим функцию , определенную на множестве и имеющую частные производные и в точке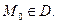

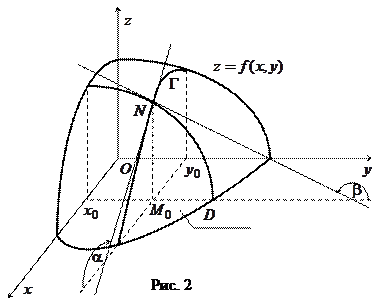Механический смысл частных производных состоит в следующем: частные производные 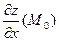и 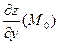равны скоростям изменения функции 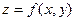в точке 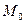в положительных направлениях координатных осе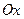й и 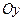соответственно. Это вытекает из определения частных производных и механического смысла обычных производных функции одной переменной.

Аналогичные утверждения применимы к частным производным функции .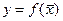

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ЧАСТНЫХ ПРОИЗВОДНЫХ

Рассмотрим функцию двух переменных 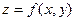, определенную на множестве 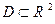и имеющую конечные частные производные 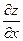и 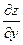в точке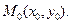

Чтобы выяснить геометрический смысл частных производных, выполним следующие построения. В плоскости 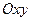отметим точку 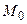(рис. 2).

Затем нарисуем поверхность 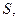являющуюся графиком функции 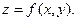Без ограничения общности будем полагать, что поверхность расположена над плоскостью 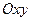. Через точку 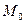проведем плоскость 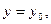параллельную координатной плоскости 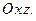В сечении поверхности 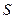этой плоскостью получаем кривую 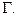Уравнение этой кривой описывается функцией одной переменной 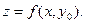Так как в точке 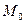существует частная производная 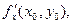то она согласно геометрическому смыслу обычной производной функции одной переменной равнаугловому коэффициенту касательной, проведенной в точке 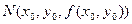к кривой :

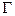где 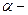угол между касательной и положительным направлением оси 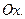В этом состоит геометрический смысл частной производной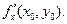

Если построить сечение поверхности 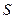плоскостью 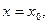то частная производная 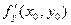равна угловому коэффициенту касательной, проведенной к графику функции в точке 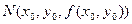в этом сечении: .

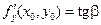ЭКОНОМИЧЕСКИЙ СМЫСЛ ЧАСТНЫХ ПРОИЗВОДНЫХ ФУНКЦИИ КОББА-ДУГЛАСА

Рассмотрим производственную функцию Кобба-Дугласа .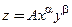

При фиксированном значении переменной 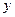частная производная 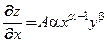равна предельной производительности труда. Она показывает, насколько вырастет объем выпускаемой продукции, если увеличить трудовые ресурсы на единицу (взять, например, дополнительно одного рабочего) при сохранении объема фондов.

При фиксированном значении переменной 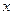частная производная 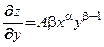равна предельной фондоотдаче. Она показывает, насколько вырастет выпуск продукции, если увеличить объем производственных фондов на единицу (например, увеличить количество станков на единицу) при сохранении объема трудовых ресурсов.