І.1. Класифікація рівнянь в частинних похідних.

ПОСТАНОВКА ЗАДАЧ МАТЕМАТИЧНОЇ ФІЗИКИ.

Перший розділ посібника присвячено класифікації рівнянь математичної фізики, виведенню таких важливих рівнянь, як рівняння теплопровідності та рівняння коливання струни, а також класифікації задач математичної фізики.

І.1. Класифікація рівнянь в частинних похідних.

Класифікацію рівнянь другого порядку проводитиметься на основі аналізу характеристичної частини рівняння. Отже, спочатку нагадаємо основні означення теорії диференціальних рівнянь частинними похідними.

Означення 1.

Співвідношення, що зв’язує незалежні змінні, шукану функцію та її частинні похідні, називають рівнянням у частинних похідних

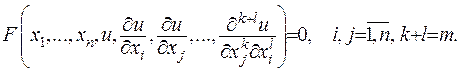(1.1)

Тут функція 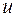така, що задана на просторі 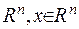, та діє таким чином

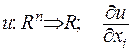- частинна похідна, що визначається за формулою

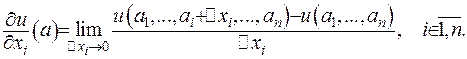
Означення 2.

Порядок старшої похідної 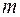, що входить у диференціальне рівняння з частинними похідними (1.1), називають порядком рівняння.

Всі фізичні процеси можна описати рівняннями у частинних похідних вигляду (1.1). Але переважна більшість процесів описується диференціальними рівняннями другого порядку, які мають вигляд:

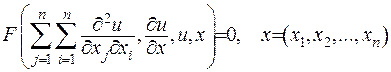. (1.2)

Означення 3.

Якщо коефіцієнти при частинних похідних другого порядку є функціями незалежних змінних 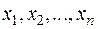та функцій 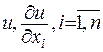, то таке рівняння називають квазілінійним рівнянням

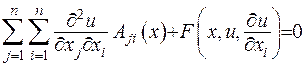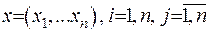, . (1.3)

Означення 4.

Якщо коефіцієнти при частинних похідних другого порядку є функціями тільки незалежних змінних 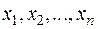, то такі рівняння називають лінійними відносно старших похідних.

Не обмежуючи міркування, будемо у наступному загальний вигляд лінійного диференціального рівняння другого порядку записувати у формі

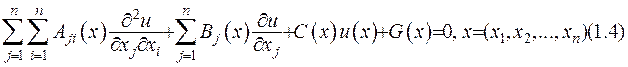
І.2. Зведення до канонічного вигляду рівнянь математичної фізики. Класифікація рівнянь математичної фізики.

Нехай маємо диференціальне рівняння у частинних похідних другого порядку

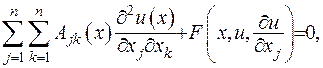(1.5)

де 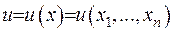. Перший доданок у лівій частині рівності (1.5) визначає тип рівняння та відповідний метод його розв’язання. Його будемо називати характеристичною частиною рівняння та у подальшому визначати як

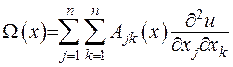. (1.6)