Проблема гетероскедастичности. Её экономические причины и методы выявления.

В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора 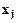остатки 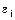имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 3.5).

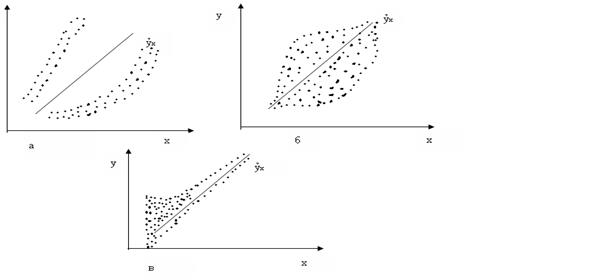
Рис 3.5 примеры гетероскедастичности:

а – дисперсия остатков растет по мере увеличения x;

б – дисперсия остатков достигает максимальной величины при средних значениях переменной x и уменьшается при минимальных и максимальных значения x,

в – максимальная дисперсия остатков при малых значениях x и дисперсия остатков однородна по мере увеличения значений x

Гомоскедастичность остатков означает, что дисперсия остатков 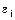одинакова для каждого значения х. используя трехмерное изображение, получим следующие графики, иллюстрирующие гомо- и гетероскедастичность (рис. 3.6, 3.7).

Рис. 3.6. Гомоскедастичность остатков

Рис. 3.7. Гетероскедастичность остатков

Рис.3.6 показывает, что для каждого значения 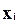распределения остатков 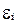одинаковы в отличие от рис. 3.7, где диапазон варьирования остатков меняется с переходом от одного значения 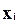к другому. Соответственно на рис. 3.7.демонстрируется неодинаковая дисперсия 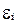при разных значениях .

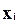Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков 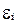от теоретических значений результативного признака 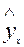. Так, для рис.3.5 а) зависимость остатков от 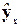представлена на рис.3.8.

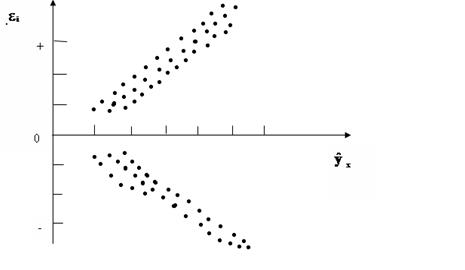
Рис.3.8.Гетероскедастичность: большая дисперсия для больших значений

Соответственно для зависимости, изображенной на полях корреляции рис. 3.5 б) и в), гетероскедастичность остатков представлена на рис.3.9 и 3.10.

Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- и гетероскедастичности.

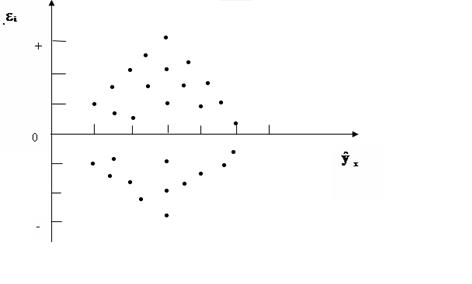
Рис. 3.9.Гетероскедастичность, соответствующая полю корреляции рис. 3.5 б)

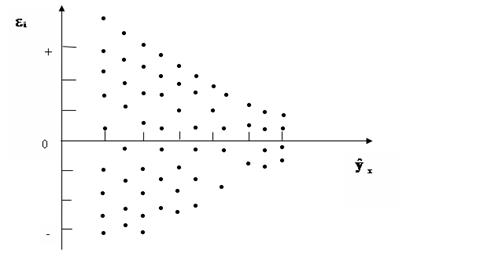
Рис. 3.10.Гетероскедастичность, соответствующая полю корреляции рис. 3.5 в)