Ознайомимось коротко з характеристиками коливальних рухів .
Коливальним рухом або просто коливанням називається всякий рух або зміна стану, що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, які визначають цей рух або стан.
Коливальний рух називається періодичним, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Періодичні коливання якої – небудь фізичної величини х називається гармонічними, якщо її залежність від часу має вигляд
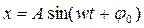 або
або 
причому 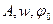 з бігом часу не змінюється.
з бігом часу не змінюється.
Амплітудою А називається фізична величина яка дорівнює максимальному зміщенню змінної величини х по відношенню положення рівноваги.
Вираз 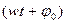 визначає зміщення х у даний момент часу і називається фазою коливань; при t=0 цей вираз стає рівним
визначає зміщення х у даний момент часу і називається фазою коливань; при t=0 цей вираз стає рівним 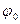 і називається початковою фазою коливань.
і називається початковою фазою коливань.
Величина w називається циклічною (або коловою) частотою коливання ; вона зв’язана з періодом Т -  та частотою
та частотою 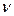 коливань -
коливань -  . Отже, як бачимо
. Отже, як бачимо 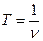 .
.
Періодом незатухаючих коливань називається той найменший проміжок часу t, після проходження якого повторюються значення всіх фізичних величин, що характеризують коливання.
Частотою коливання  називається число повних коливань, що здійснюється за одиницю часу.
називається число повних коливань, що здійснюється за одиницю часу.
 Швидкість та прискорення при гармонічному коливанні величини змінні і визначаються так :
Швидкість та прискорення при гармонічному коливанні величини змінні і визначаються так :
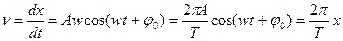
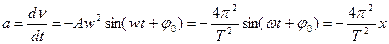
Мінус в останньому виразі означає, що прискорення завжди спрямоване в сторону, протилежну до зміщення.
|
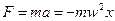
Якщо позначити 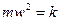 , то одержимо
, то одержимо 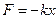 , тобто в коливальних рухах діють пружні або квазіпружні сили.
, тобто в коливальних рухах діють пружні або квазіпружні сили.
|
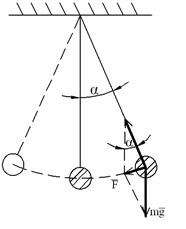
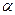 кульку з масою m діє дві сили - вага Р і сила N з боку нитки, їх рівнодійна F спрямована в сторону положення рівноваги. Це і є повертаюча сила
кульку з масою m діє дві сили - вага Р і сила N з боку нитки, їх рівнодійна F спрямована в сторону положення рівноваги. Це і є повертаюча сила  . З рисунка
. З рисунка 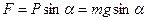 . При малих відхиленнях
. При малих відхиленнях 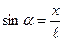 ; отже,
; отже, 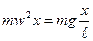 а
а 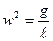 . Якщо врахуємо зв’язок w і Т, то одержимо
. Якщо врахуємо зв’язок w і Т, то одержимо 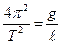 і остаточно
і остаточно 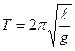 .
.
Всі реальні коливальні системи є дисипативними – запас їх механічної енергії поступово зменшується, перетворюючись в інші не механічні форми енергії, з часом коливання згасають. Але, знаючи, що сили опору, які діють при коливаннях математичного маятника, порівняно незначні, ми можемо вважати ці коливання гармонічними.
Як видно з останньої формули період коливання маятника не залежить від кута відхилення (беремо 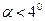 ) та від маси маятника. Знаходимо прискорення :
) та від маси маятника. Знаходимо прискорення :
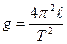
Для виконання дослідів математичний маятник виготовляється так : підвішують на тонкій, міцній нитці важку металеву кульку. Маса нитки дуже мала порівняно з масою кульки. Тому нею можна нехтувати, а за довжину маятника береться віддаль від верхньої точки закріпленої нитки до центра кульки (центр кульки збігається з центром коливання маятника).Тоді довжина маятника 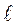 буде дорівнювати довжині нитки плюс радіус кульки r,
буде дорівнювати довжині нитки плюс радіус кульки r,
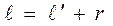 (5)
(5)
Підставляючи значення  з формули (5) в формулу (4) дістанемо:
з формули (5) в формулу (4) дістанемо:
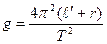 (6)
(6)
Дата добавления: 2016-05-16; просмотров: 1107;
