Предпосылки музыкальной выразительности метра
Существуют две основные разновидности метра — двухдольный и трехдольный. Двухдольный представляет собой равномерное чередование одной сильной и одной слабой долей. Он может быть изображен следующей схемой, где сильная доля представлена знаком —, а слабая — знаком 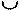 :
:
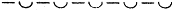 и т.д.
и т.д.
Трехдольный метр представляет собой чередование одной сильной доли с двумя слабыми:
 и т.д.
и т.д.
Двухдольный метр является более простым, более естественным, более четким. Его естественность коренится в очень многих жизненных и природных явлениях, связанных с равномерным движением, равномерной пульсацией*[«Двухдольной» является ходьба человека, биение его сердца и т. п. Интересно заметить, что вообще любую равномерную пульсацию мы склонны воспринимать как двухдольную. В совершенно равномерном тиканье часов мы слышим двухдольное «тик-так». Но если специально настроить себя на трехдольность можно услышать в тиканье часов и ее. Можно заставить себя услышать в часах и пятидольность. Но двухдольность нам кажется более естественной.] Практически трехдольный метр почти не имеет аналогий в природе и жизненных явлениях. Увеличение, по сравнению с двухдольным метром, количества слабых долей делает его менее четким, более плавным, смягченным. Четкость и активность двухдольного, плавность и мягкость трехдольного метров — естественные предпосылки музыкальной выразительности, которые наиболее ярко проявляют себя в важнейших музыкальных жанрах, связанных с двухдольностью (например, марш) и с трехдольностью (например, вальс).
Метрические стопы
Сочетание сильной и слабой долей в двухдольном и сильной и двух слабых долей в трехдольном метрах образуют стопу. Стопы различаются положением сильных долей по отношению к слабым. Так, в двухдольном метре оказываются возможными две стопы:
 и
и 
В трехдольном метре таких возможностей три:
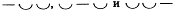
Сам термин «стопа» заимствован из теории стихосложения, где он означает характер сочетания ударных и неударных слогов. Из стихосложения же заимствованы и названия различных стоп:
 ямб,
ямб,
 хорей,
хорей,
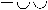 дактиль,
дактиль,
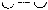 амфибрахий,
амфибрахий,
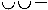 анапест.
анапест.
В широком смысле они группируются в ямбические (ямб и анапест) и хореические (хорей и дактиль) стопы. Амфибрахий занимает промежуточное положение между ними.
Метрические стопы проявляют себя в ритмическом рисунке в виде соотношения акцентируемых и неакцентируемых длительностей.
Размер и такт
Очень близко понятию метра понятие размера. Если метр определяет лишь двухдольность или трехдольность, то размер представляет собой конкретизацию метра, то есть связывает метр с определенной длительностью долей. Так, метрическая основа может быть одинаковой, а продолжительность долей разной: они могут быть выражены половинными, четвертями, восьмыми и другими длительностями. Цифровое выражение размера называется показателем размера. Обычно оно обозначается двумя арабскими цифрами, расположенными строго вертикально* [Исключение составляют знаки С, соответствующий размеру 4/4, и 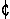 (alla breve), соответствующий, как правило, размеру 2/2]. Верхняя цифра показателя размера указывает количество метрических долей, а нижняя — продолжительность каждой доли.
(alla breve), соответствующий, как правило, размеру 2/2]. Верхняя цифра показателя размера указывает количество метрических долей, а нижняя — продолжительность каждой доли.
Размеры подразделяются на простые, сложные однородные и сложные смешанные. В простых размерах содержится только одна метрическая ячейка: двухдольная или трехдольная. Таким образом, в простых размерах верхняя цифра показателя — 2 или 3 — совпадает с числом долей метра: 2/2, 2/4, 2/8, 2/16, 3/2, 3/4, 3/8, 3/16. В сложных однородных размерах содержатся две, три, четыре метрических ячейки с одинаковой продолжительностью долей, например: 4/4=2/4+2/4, 6/8=3/8+3/8, 4/8=2/8+2/8, 12/8=3/8+3/8+3/8+3/8, 6/4=3/4+3/4 и т.д.
Сложные смешанные размеры представляют собой объединение неодинаковых метрических ячеек с одинаковой продолжительностью счетных долей, например: 5/8=2/8+3/8 (чаще) или 3/8+2/8 (реже), 5/4=2/4+3/4 (чаще) или 3/4+2/4(реже), 7/8 3/8+2/8+2/8 (или наоборот) и т. п. В сложных, как однородных, так и смешанных размерах оказываются, таким образом, две, а иногда и три сильные доли, совпадающие с первыми долями составляющих их метрических ячеек. Первая из них является основной сильной долей, последующие — относительно сильными долями. Так, например, в размере 6/8 первая восьмая оказывается основной сильной долей, а четвертая — относительно сильной. В сложных смешанных размерах могут быть варианты относительно сильных долей. Так, например, в размере 5/8 (или 5/4) относительно сильной может оказаться либо третья доля (в случае: 5=2+3), либо четвертая доля (в случае: 5=3+2).
Кроме описанных выше, в музыке встречаются также и переменные размеры. Переменным называется размер с изменяющимся количеством счетных долей.
Если чередование (смена) определенных размеров в произведении производится строго систематически, то такой переменный размер называется периодическим. В этом случае в начале пьесы сразу выставляются обозначения обоих (или нескольких) размеров в соответствии с порядком их чередования. Если же смена различных размеров будет происходить лишь эпизодически, то есть без определенной системы, то данный размер называется непериодическим переменным размером. В таком случае внутри пьесы всякий раз выставляется обозначение вновь наступившего размера (прим. 32—33).
Переменные размеры весьма характерны, в частности, для русских протяжных народных песен; нередко они встречаются в композиторском творчестве (например; в произведениях Римского-Корсакова, Скрябина, Стравинского и др.).
Дата добавления: 2016-05-16; просмотров: 644;
