Алгоритм последовательного размещения графа в решетке
1. Записать матрицу Rграфа G.Переход к 2.
2. Вычислить степени вершинr(xi), iÎI . Переход к 3.
3. Выбрать элемент с  r(ei)=min. Переход к 4.
r(ei)=min. Переход к 4.
4. Поместить элемент ei в текущий узел рt. Переход к 5.
5. Вi-й строке матрицы R выбрать элемент rij с максимальным значением и вершину xiпоместить в следующий узел решетки рt+1.Заменить rij и rji нулями. Переход к 6.
6. Рассмотреть строку, соответствующую еj, положить j=i (j=1,2,…,k) и перейти к 5. Если на каком-то шаге все элементы строки еnматрицы Rравны нулю, то необходимо вернуться на n-1, n-2, … шаг, пока не произойдет возврат к строке, в которой будет присутствовать хотя бы один ненулевой элемент.
7. Получено упорядоченное размещение вершин графа в решетке.
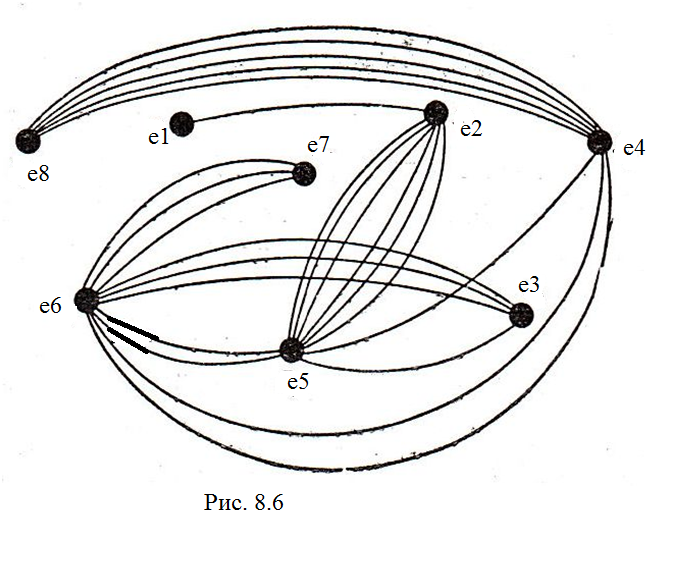
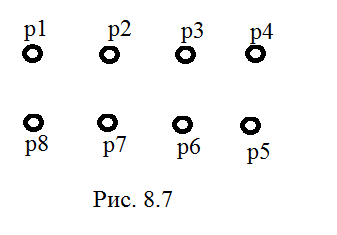
Пусть задан граф, приведенный на рис. 8.6 и дана решетка с размерами 4х2 (рис.8.7). Разместить вершины графа в узлах решетки.
1. Записываем матрицу смежности графа.
2. Подсчитываем степени вершин.
| R= | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | ||
| e1 | r(e1) =1 | |||||||||
| e2 | r(e2) =7 | |||||||||
| e3 | r(e3) = 4 | |||||||||
| e4 | r(e4) = 8 | |||||||||
| e5 | r(e5) = 10 | |||||||||
| e6 | r(e6) = 10 | |||||||||
| e7 | r(e7) = 3 | |||||||||
| e8 | r(e8) = 5 |
3. Выбираем элемент  r(ei)=min=1- это элемент e1.
r(ei)=min=1- это элемент e1.
4. Помещаем элемент e1 в узел р1.
5. В 1-й строке матрицы смежности выбираем r12=1=max.Помещаем элемент e2 в узел р2.Заменяемr12 иr21 на0.Матрица смежности принимает вид:
| R= | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | ||
| e1 | ||||||||||
| e2 | ||||||||||
| e3 | ||||||||||
| e4 | ||||||||||
| e5 | ||||||||||
| e6 | ||||||||||
| e7 | ||||||||||
| e8 |
6. Рассматриваем строку, соответствующую e2.Переход к 5.
5`. Во2-й строке матрицы смежности выбираем r25=6=max.Помещаем элемент e5 в узел р3.Заменяемr25 иr52 на0.
Матрица смежности принимает вид:
| R= | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | ||
| e1 | ||||||||||
| e2 | ||||||||||
| e3 | ||||||||||
| e4 | ||||||||||
| e5 | ||||||||||
| e6 | ||||||||||
| e7 | ||||||||||
| e8 |
6`. Рассматриваем строку, соответствующую e5.Переход к 5.
5``. В5-й строке матрицы смежности выбираем r56=2=max.Помещаем элемент e6 в узел р4.Заменяемr56иr65на0.
Матрица смежности принимает вид:
| R= | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | ||
| e1 | ||||||||||
| e2 | ||||||||||
| e3 | ||||||||||
| e4 | ||||||||||
| e5 | ||||||||||
| e6 | ||||||||||
| e7 | ||||||||||
| e8 |
6``. Рассматриваем строку, соответствующую e6.Переход к 5.
5```. В6-й строке матрицы смежности выбираем r63=3=maxПомещаем элемент e3 в узел р5.Заменяемr36 иr63 на0.
Матрица смежности принимает вид:
| R= | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | ||
| e1 | ||||||||||
| e2 | ||||||||||
| e3 | ||||||||||
| e4 | ||||||||||
| e5 | ||||||||||
| e6 | ||||||||||
| e7 | ||||||||||
| e8 |
6```. Рассматриваем строку, соответствующую e3.Переход к 5.
5````. r35=1=maxне рассматривается, т.к. e3 иe5уже помещены в узлы решетки.
Возвращаемся к 6-й строке. Выбираем r67=5=max.Помещаем элемент e7 в узел р6.Заменяемr67 иr76 на0.
Матрица смежности принимает вид:
| R= | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | ||
| e1 | ||||||||||
| e2 | ||||||||||
| e3 | ||||||||||
| e4 | ||||||||||
| e5 | ||||||||||
| e6 | ||||||||||
| e7 | ||||||||||
| e8 |
6````. Рассматриваем строку, соответствующую e7.Переход к 5.
5`````. В 7-й строке матрицы все элементы нулевые, поэтому возвращаемся к 6-й строке.
Выбираем r64=2.Помещаем элемент e4 в узел р7.
6````. Оставшийся элемент e8 помещаем в узел р8.
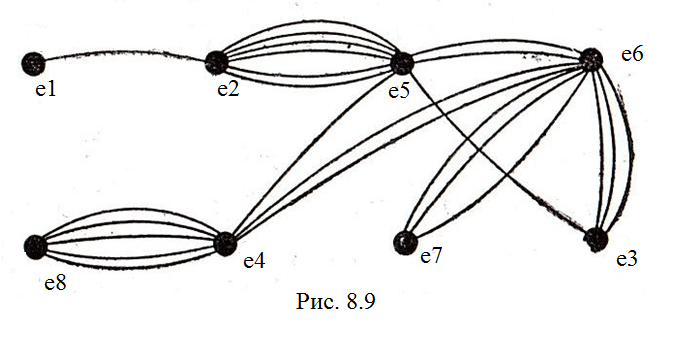
Результат приведен на рис. 8.9.
Оглавление
Лекция 8. 1
Алгоритмы размещения элементов. 1
Конструктивные алгоритмы начального размещения. 3
Этап 1. Выбор элемента. 5
Этап 2. Выбор позиции. 7
Правило выбора первого элемента. 10
Итерационные алгоритмы улучшения начального размещения. 13
Алгоритм парных перестановок. 15
Непрерывно-дискретные методы размещения. 18
Пример алгоритма последовательного размещения. 19
Алгоритм последовательного размещения графа в решетке. 20
Дата добавления: 2016-05-16; просмотров: 2099;
