Отрицательные двоичные числа

Самый простой метод представления отрицательных чисел – отвести один бит (логичнее всего – старший) для хранения знака. По причинам, которые вы поймете далее, значение 1 в этом бите означает знак «минус», а 0 – знак «плюс». Что произойдет с нашим числом при таком представлении?

В области положительных чисел не произойдет ничего, кроме того, что их диапазон сократится вдвое, – например, для числа в байтовом представлении вместо диапазона 0…255 мы получим всего лишь 0…127 (0000 0000–0111 1111). А отрицательные числа будут иметь тот же диапазон, только старший бит у них будет равен 1. Все просто, не правда ли?

Нет, неправда. Такое представление отрицательных чисел совершенно не соответствует обычной числовой оси, на которой влево от нуля идет минус единица, а затем числа по абсолютной величине увеличиваются. Здесь же мы получаем, во‑первых, два разных нуля («обычный» 0000 0000 и «отрицательный» 1000 0000), во‑вторых, оси отрицательных и положительных чисел никак не стыкуются, и производство арифметических операций превратится в головоломку. Поэтому поступим так: договоримся, что ‑1 соответствует число 255 (1111 1111), – 2 – число 254 (1111 1110) и т. д. вниз до 128 (1000 0000), которое будет соответствовать ‑128 (и общий диапазон всех чисел получится от ‑128 до 127). Очевидно, что если вы при таком представлении хотите получить отрицательное число в обычном виде, то надо из значения числа (например, 240) вычесть максимальное значение диапазона (255) плюс 1 (256). Если отбросить знак, то результат такого вычитания (16 в данном случае) называется еще дополнением до 2 для исходного числа (а само исходное число 240 – дополнением до 2 для 16). Название «дополнение до 2» используется независимо от разрядности числа, потому что верхней границей всегда служит степень двойки (в десятичной системе аналогичная операция называется «дополнение до 10»).

Что произойдет в такой системе, если вычесть, например, 2 из 1? Запишем это действие в двоичной системе обычным столбиком:

В первом разряде результата мы без проблем получаем 1, а уже для второго нам придется занимать 1 из старших, которые сплошь нули, поэтому представим себе, что у нас будто бы есть девятый разряд, равный 1, из которого заем в конечном итоге и происходит:

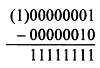
На самом деле девятиразрядное число 1 0000 0000 есть не что иное, как 256, т. е. то же самое максимальное значение плюс 1, и мы здесь выполнили две операции: прибавили к уменьшаемому эти самые 256, а затем выполнили вычитание, но уже в положительной области для всех участвующих чисел.

А что результат? Он будет равен 255, т. е. тому самому числу, которое, как мы договорились, и представляет – 1. Получается, что вычитание в такой системе происходит автоматически правильно, независимо от знака участвующих чисел. Если хотите, можете потренироваться и проверить, скажем, что будет, если в этой системе вычесть 240 из 100.

Немного смущает только эта самая операция нахождения дополнения до 2, точнее, в данном случае, до 256 – как ее осуществить на практике, если схема всего имеет 8 разрядов? В дальнейшем мы увидим, что иногда ее осуществлять вовсе не надо – некоторые электронные схемы ведут себя так, что при осуществлении вычитания вся процедура осуществляется автоматически. Особенно наглядно это выглядит для двоичных реверсивных счетчиков, которые мы будем рассматривать в главе 16 .

В точности так же ведут себя и соответствующие команды в микропроцессорах – и если вы захотите произвести операцию вычитания числа 2 из содержимого восьмибитового регистра, содержащего число 1, то в регистре окажется число 255 (все единицы). А интерпретация результата – как отрицательного числа или как положительного – это уже ваши трудности.

В микропроцессорах есть обычно и команда, которая возвращает дополнение до 2, в большинстве ассемблеров она называется NEG, от слова «негативный», потому что меняет знак, если мы договариваемся считать числа «со знаком». А как ее можно было бы осуществить «вручную», не обращаясь в действительности к 9‑му разряду? Вернемся к рассмотренным ранее примерам и выпишем столбиком исходные числа, результаты операции нахождения дополнения до 2 и результат еще одной манипуляции, которая представляет собой вычитание единицы из дополнения до 2, т. е., что то же самое, просто вычитания исходного числа из наивысшего числа диапазона (255):

Если мы сравним двоичные представления в верхней и нижней строках, то увидим, что они могут быть получены друг из друга путем инверсии каждого из битов. Эта операция называется нахождением дополнения до 1 (потому что число, из которого вычитается, содержит все 1 во всех разрядах; для десятичной системы аналогичная операция называется дополнение до 9 ). Для нахождения дополнения до 1 девятый разряд не требуется, да и схему можно построить так, чтобы никаких вычитаний не производить, а просто переворачивать биты. То есть, для полного сведения вычитания к сложению надо проделать три операции:

1. Найти дополнение до 1 для вычитаемого (инвертировать его биты).

2. Прибавить к результату 1, чтобы найти дополнение до 2.

3. Сложить уменьшаемое и дополнение до 2 для вычитаемого.

Заметим, что все сложности с этими многочисленными дополнениями связаны с наличием нуля в ряду натуральных чисел – если бы его не было, дополнение было бы всего одно, и операция вычитания упростилась. Так может, греки все же были в чем‑то правы?

В заключение обратим внимание на еще одно замечательное свойство двоичных чисел, которое часто позволяет значительно облегчить операции умножения и деления, а именно: умножению на 2 соответствует операция сдвига всех разрядов числа на один разряд влево, а операции деления на 2 – вправо. Крайние разряды (старший при умножении и младший при делении) в общем случае при этом должны теряться, но в микропроцессорах есть специальный бит переноса, в который эти «потерянные» разряды помещаются. Противоположные крайние разряды (младший при умножении и старший при делении) в общем случае замещаются нулями, но могут и замещаться значением бита переноса, что позволяет без лишних проблем делить и умножать числа с разрядностью больше одного байта. Как можно догадаться, умножению и делению на более высокие степени двойки будет соответствовать операция сдвига в нужную сторону на иное (равное степени) число разрядов.

Излишне говорить, что операцию сдвига разрядов в электронных схемах производить неизмеримо проще, чем операции деления и умножения. Есть и специальные схемы для этой операции – сдвиговые регистры, которые мы также будем «проходить» (в главе 16 ).

Дробные числа

Сразу заметим, что в некомпьютерной электронике дробными числами стараются не пользоваться. При необходимости их переводят в целые, умножая на соответствующую степень десяти (а чаще – даже на степень 2, что проще), при этом все остальные участвующие в расчетах величины также масштабируются в нужное число раз. Затем при выводе, к примеру, на цифровой дисплей, запятая просто устанавливается в нужном месте (иногда заранее, и без возможности изменения ее положения). То есть, для цифровой схемы не существует значения температуры, равного 30,81 градуса, а есть число 3081 в BCD‑формате. Примерно те же действия мы производили, когда конструировали цифровой термометр в главе 13 , – на самом деле он показывает целое число милливольт в нужном масштабе.

И все же – как мы можем при необходимости представить дробные числа, если двоичные разряды ничего о таковых «не знают» и могут воспроизводить только целые числа в соответствии с формулой (4)? Мы не будем рассматривать расширение этой формулы, включающее в себя представление в позиционной системе не только целых, но и всех действительных чисел «с плавающей запятой», т. к. в электронике такой вариант не хождения не имеет. В электронике и компьютерной технике используют другой способ представления действительных чисел – с помощью мантиссы и порядка, в так называемом нормализованном виде . При этом место запятой фиксируется:

0,0125 = 0,125·10^‑1,

1254,81 =0,125481·10⁴.

Разумеется, в электронных схемах все это лучше делать в двоичной форме, записывая порядок, как степень двух (скажем, операция выравнивания порядков при сложении таких чисел сведется просто к сдвигу мантиссы, как мы видели ранее).

Легко заметить, что и саму запятую, и основание степени тут можно опустить, записывая в память лишь мантиссу и порядок – конечно, если всегда помнить, что мы имеем в виду. Например, можно сделать так: отвести в памяти три байта, из которых первые два хранят цифры мантиссы, а третий отведен под порядок. Легко также подсчитать, каков будет диапазон чисел, могущих быть представленными таким образом, – число, которое представляет мантиссу, будет укладываться в диапазон от ‑32768 до 32767, т. е. иметь от 4 до 5 значащих десятичных цифр. На практике операции с дробными числами можно производить несколько проще, и мы будем их осваивать в главе 20 .