Двоичный сумматор на логических микросхемах

Заметим сразу, что схема этого устройства в том виде, в котором мы ее сейчас будем конструировать, сама по себе довольно бесполезна – если вы, конечно, не хотите повторить подвиг советского конструктора Михаила Александровича Карцева. Он создал в 1970‑х годах на микросхемах малой степени интеграции (т. е. фактически на отдельных логических элементах) очень удачную ЭВМ под названием М‑10, замечательную тем, что отдельные ее экземпляры в нашем оборонном комплексе продержались аж до начала нового тысячелетия. При желании повторить такой подвиг, учтите, что основная проблема, которую вам придется решать, состоит вовсе не в том, чтобы такую машину сконструировать схемотехнически – это не самая трудная часть работы. Самое трудное для подобных суперконструкций – решить проблему отвода тепла, выделяемого сотнями тысяч быстродействующих логических микросхем. Суперкомпьютеры Cray на отдельных логических элементах, выпускаемые в 1980‑х годах, даже имели водяное охлаждение.

Наконец, если очень хочется, то готовый двоичный сумматор есть в интегральном исполнении (561ИМ1; есть сумматоры и помощнее). Зачем же мы тогда будем его конструировать? А затем, что его устройство очень хорошо иллюстрирует две вещи: во‑первых, само применение логических микросхем, во‑вторых – разве не любопытно знать, как устроен самый главный узел компьютера, арифметико‑логическое устройство, АЛУ? Знание этого вам очень пригодится для лучшего понимания работы микроконтроллеров и принципов их программирования. Кроме того, мы на этом примере познакомимся еще с одним важным типом логических элементов.

Итак, вспомним, что нам, собственно, нужно делать – а именно: воспроизвести таблицу сложения двоичных чисел, которая была показана для одноразрядных чисел в главе 14 . Так как при сложении единиц получается двухразрядное двоичное число, то перепишем эту таблицу в двухразрядном представлении:

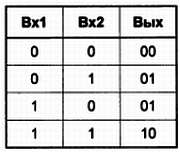
Теперь разобьем таблицу на две: одну для разряда собственно суммы, другую для значения переноса в следующий разряд:

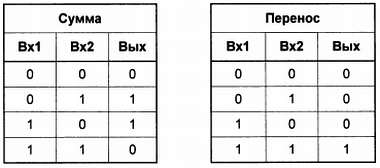
Сравним вторую таблицу с таблицей состояний для базовых логических функций (я их повторю, чтобы не пришлось листать книгу):

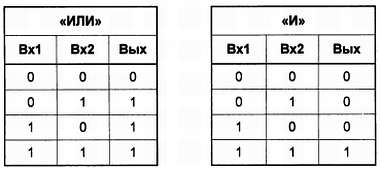
Для переноса имеем полное совпадение с функцией «И». То есть, для того чтобы обеспечить перенос, нам нужен всего лишь один логический элемент «И», который получается комбинированием стандартного «И‑НЕ» с инвертором[21]. Хуже с разрядом суммы: первые три значения обеспечивает элемент «ИЛИ», однако при сложении единиц возникает несоответствие (логическое и арифметическое сложения, как мы говорили, не адекватны друг другу). Нужен специальный элемент, который мог бы получить название элемент несовпадения : в самом деде, у него логическая единица на выходе тогда, когда входы имеют разное состояние, а если они одинаковы – на выходе ноль. Для того чтобы его сконструировать, взглянем на таблицу истинности элемента «И‑НЕ» (для наглядности я повторю и ее):

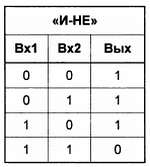
Сравним таблицы «ИЛИ», «И‑НЕ» и необходимой нам суммы: в первом случае мы получаем то, что надо, в верхних трех строках, во втором – в нижних. Как бы их объединить? Да очень просто – через функцию «И»:

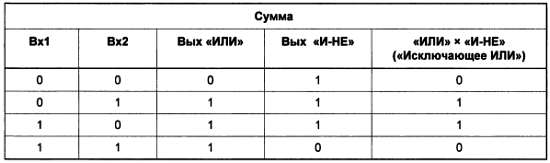
Логический элемент с такой функцией «несовпадения» носит специальное название – «Исключающее ИЛИ». Существует и обратный элемент «совпадения», который представляет собой инверсию выхода «Исключающего ИЛИ» и носит название «Включающего ИЛИ».

Обозначение элемента «Исключающее ИЛИ» уже было показано на рис. 15.3. А как можно его составить из элементов «И‑НЕ» и «ИЛИ‑НЕ», показано на рис. 15.5.

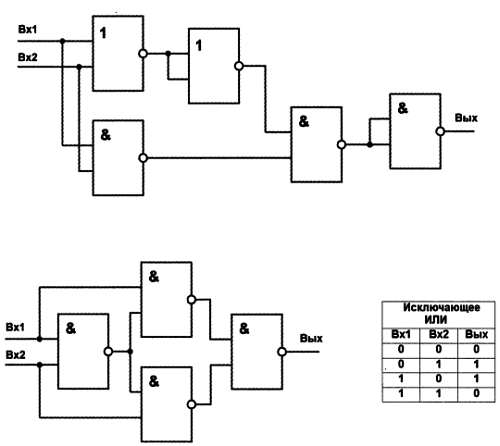
Рис. 15.5. Варианты реализации элемента «Исключающее ИЛИ» и его таблица истинности

Верхний вариант полностью соответствует нашим рассуждениям и потребует двух корпусов микросхем, а нижний вариант – пример того, как можно построить «Исключающее ИЛИ» с использованием только одного типа элементов, в данном случае – «И‑НЕ». Он более экономичен, т. к. потребует всего одного корпуса типа 561ЛА7. Попробуйте построить таблицу истинности для второго варианта, и вы убедитесь, что он работает «как заказывали» (есть и много других способов). Отметьте, что в первом варианте специальных элементов‑инверторов мы не используем, а с целью экономии корпусов микросхем образуем их из элементов «И‑НЕ» или «ИЛИ‑НЕ» путем объединения входов – обычно так и поступают.

В любой логической серии есть, разумеется, и специальные микросхемы «Исключающее ИЛИ» (561ЛП2). Элемент «Исключающее ИЛИ», помимо способности выдавать сумму одноразрядных чисел, обладает многими интересными свойствами, к которым мы обратимся далее, а пока вернемся к сумматору.

На самом деле одноразрядный сумматор мы уже построили. Его схема приведена на рис. 15.6 вверху . Внизу на рис. 15.6 мы обозначили все устройство одним квадратиком.

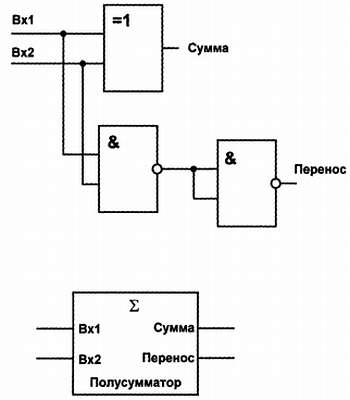
Рис. 15.6. Схема одноразрядного полусумматора

Однако почему там написано «полусумматор»? Такой одноразрядный сумматор носит название полусумматора, потому что он не «умеет» одной важной вещи, а именно: разряд переноса‑то он выдает, а вот учесть перенос от предыдущего разряда не может. Поэтому, чтобы складывать многоразрядные числа по‑настоящему, нужно в каждом разряде поставить по два таких полусумматора, причем объединить их выходы переносов через «ИЛИ» (рис. 15.7).

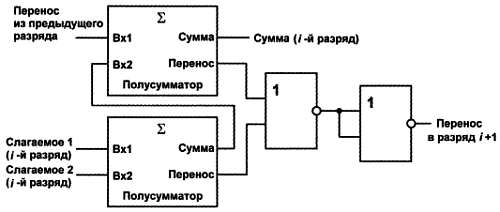
Рис. 15.7. Схема многоразрядного сумматора

Так мы получили одноразрядный полный сумматор. Объединением таких сумматоров несложно соорудить устройство для сложения чисел любой разрядности. Если вы попробуете нарисовать схему сумматора для, скажем, восьми разрядов полностью с использованием принципиальных схем логических элементов по рис. 15.1, то ужаснетесь – это же сколько транзисторов надо, чтобы построить такое устройство? Много – в восьмибитном КМОП‑сумматоре их получается 480 штук (а современные микросхемы, бывает, содержат и больше транзисторов). И это без учета того, что в систему должны входить еще, как минимум, два регистра для хранения исходных чисел и результата (в целях экономии результат помещают в регистр одного из слагаемых, тем самым слагаемое это уничтожая), а также другие логические схемы (для сдвига, для инверсии битов при манипуляции с отрицательными числами). То есть общее количество транзисторов составляет порядка тысячи.

Теперь понятно, почему микросхемы высокой степени интеграции содержат миллионы транзисторов и почему проблема отвода тепла стоит так остро! Один логический элемент КМОП из четырех транзисторов выделяет, согласно рис. 15.2, при частоте в единицы мегагерц всего‑навсего полмилливатта тепла, но что будет, если таких элементов приходится ставить в количестве миллион штук? И еще при этом как можно больше повышать рабочую частоту?

Сумматоры, построенные по описанной схеме, выпускают, естественно, в интегральном исполнении (в «классической» КМОП это микросхема четырехразрядного сумматора 561ИМ1, есть и схема более универсального АЛУ – 561ИПЗ). В связи с многоразрядным сумматором возникает только один вопрос – а что делать с входом переноса самого первого, младшего разряда? Если мы просто складываем двоичные числа разрядности, соответствующей возможностям нашего сумматора (например, восьмиразрядные, т. е. длиной в один байт), то вход переноса младшего разряда присоединяется к логическому нулю. Соответственно, выход переноса старшего разряда остается «висеть в воздухе». Легко сообразить, что при этом, если складываются числа, в сумме составляющие более величины диапазона, старший разряд суммы «потеряется». Это явление при всей своей очевидности стоит того, чтобы рассмотреть его подробнее.

Предположим, у нас есть такой байтовый сумматор, и под числами мы имеем в виду обычные беззнаковые положительные числа, диапазон которых составит 0‑255. Если мы сложим 128 (1000 0000) и 128 (1000 0000), то получим число 256 (1 0000 0000), которое имеет единицу в 9‑м, отсутствующем у нас, разряде (заодно отметим этот результат как хорошую иллюстрацию к положению, гласящему, что умножение на 2 есть просто сдвиг всех разрядов влево на одну позицию). Таким образом, в разрядах сумматора мы получаем одни нули, что, конечно, есть результат некорректный. Для корректного сложения, к примеру, восьмибитовых чисел цам надо иметь 9 разрядов результата.

А как наращивать разряды, если, например, в микроконтроллере все регистры восьмиразрядные? Да очень просто – надо взять два таких регистра и соединить выход переноса одного со входом переноса другого. Тогда мы получим двухбайтовое число (или слово, как его чаще называют). В микропроцессорах, в том числе и в микроконтроллерах, мы, конечно, физически такое объединение сделать не можем – схема уже создана заранее, но в них зато есть специальный отдельный бит переноса (carry bit ), в который автоматически помещается перенос в результате операций сложения, умножения и, кстати, вычитания и деления тоже.