Однополярный регулируемый источник питания

Схема на рис. 9.12 представляет собой лабораторный источник питания, который, как я обещал вам еще в главе 2 , можно изготовить самим. Взглянув на эту схему, вы можете сначала слегка растеряться – настолько вам покажется все незнакомо. На самом деле там есть только одна вещь, которую мы еще «не проходили», – микросхема операционного усилителя (ОУ) DA1. Подробно с ОУ мы будем знакомиться в главе 12, а сейчас нам важно только вот что: ОУ всегда стремится сделать так, чтобы потенциалы входов, обозначенных «плюс» и «минус», были равны. Эти входы эквивалентны входам дифференциального усилителя, у которого, как вы помните, потенциалы входов тоже связаны между собой (на самом деле внутри микросхемы на входе ОУ действительно стоит дифференциальный каскад).

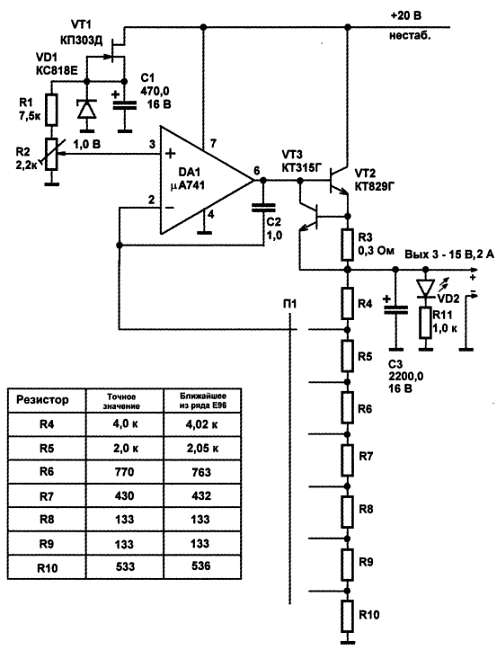
Рис. 9.12. Схема лабораторного источника питания

Для того чтобы это осуществлялось на практике, ОУ включают с отрицательной обратной связью с выхода на тот вход, который обозначен знаком «минус». В схеме, показанной на рис. 9.12, такая связь осуществляется весьма заковыристым способом, и для того чтобы понять, как это происходит, давайте посмотрим на рис. 9.13, на котором изображена та же самая схема, но в предельно упрощенном варианте.

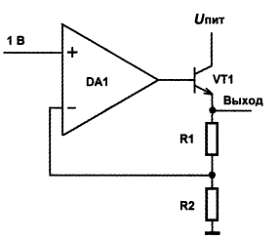
Рис. 9.13. Упрощенная схема лабораторного источника питания

Предположим, что R1 и R2 на рис. 9.13 равны между собой. Какое напряжение будет на выходе, т. е. на эмиттере транзистора VT1? Определить это очень просто. Если на «плюсовом» входе ОУ напряжение 1 В, как обозначено на схеме, то на минусовом тоже должен быть 1 В, как мы только что узнали. При каком условии это возможно? Только если на верхнем выводе R1, т. е. на выходе всей системы, будет 2 В – ведь R1 и R2 делят это напряжение пополам. То есть ОУ автоматически установит на базе транзистора VT1 такое напряжение, чтобы на его эмиттере было ровно 2 В (можно даже догадаться, какое именно – на 0,6 В больше, чем на выходе, т. е. 2,6 В, но на самом деле это нас мало интересует). А если предположить, что R1 в два раза больше, чем R2? Повторив предыдущие рассуждения, мы обнаружим, что на выходе должно быть 3 В. Отсюда можно вывести некоторую закономерность: система, показанная на рис. 9.13, усиливает напряжение, поданное на «плюсовой» вход, ровно в (R1/R2 +1) раз.

Именно так и работает схема источника на рис. 9.12. Переключатель П1 имеет 6 положений, в каждом из которых он изменяет соотношение делителя в обратной связи таким образом, чтобы при напряжении 1 В на «плюсовом» входе на выходе получался некий ряд фиксированных напряжений. При указанных в таблице номиналах резисторов R4‑R10 этот ряд будет следующим: 3; 5; 7,5; 10; 12 и 15 В, чего достаточно для большинства наших нужд.

Конечно, можно не возиться с переключателем и подбором сопротивлений, а просто поставить вместо цепочки R5‑R9 переменный резистор, равный сумме этих сопротивлений, по схеме потенциометра – эффект будет таким же, только напряжение станет меняться плавно: от 3 до 15 В. Однако иметь набор фиксированных напряжений намного удобнее – тут вы получите точно известное напряжение, а при плавной регулировке его каждый раз придется подгонять по вольтметру. Разумеется, бывают изредка ситуации, когда нужно получить напряжение, скажем, 4,75 вольта, но на этот случай лучше завести отдельный плавно регулируемый источник.

Делитель можно устроить совершенно по‑разному – возьмите переключатель на 12 положений – получите переключение через 1 В. Пересчитать номиналы резисторов из описанного ранее общего соотношения несложно: так, если хочется вместо 10 В в приведенном ряду иметь 9 В, то номинал R8 следует увеличить до 224 Ом, a R7 – уменьшить до 205 Ом (при этом сумма сохранится, и остальные напряжения не изменятся). Можно добавить переменный резистор и плавно регулировать напряжение внутри каждого фиксированного диапазона. (Подумайте, как это сделать? Подсказка: переключатель должен быть на два направления.) Отметим, что в этой схеме применять прецизионные резисторы С2‑29В совершенно необязательно – не те точности требуются. Поэтому можно требуемые номиналы просто подобрать из набора обычных, стараясь выдержать их как можно ближе к расчетным. Допускается также весь расчетный ряд умножить или поделить на любое число, лишь бы все значения изменились в одинаковой степени. Границы, которыми следует при этом руководствоваться, – это нижний предел суммы всех резисторов в 1–2 кОм, а верхний – в пару десятков килоом.

Теперь перейдем к подробному рассмотрению остальных, вспомогательных узлов схемы. Монструозная конструкция с полевым транзистором наверху на самом деле всего лишь узел, который позволяет получить стабильное опорное напряжение ровно 1В – от его стабильности точность шкалы выходных напряжений зависит напрямую.

В педагогических целях рассмотрим подробнее, как работает такая древняя схема. Полевой n ‑канальный транзистор VT1 включен источником тока, известным нам из главы 6 – когда потенциалы затвора и истока равны, то ток сток‑исток мало зависит от напряжения на стоке. Этот ток питает прецизионный стабилитрон VD1 типа КС818Е, напряжение которого мало зависит от температуры (но очень даже зависит от тока). Если будете искать замену транзистору VT1, то в первую очередь надо смотреть на параметр, который называется начальный ток стока – именно такой ток будет протекать через стабилитрон в этой схеме, а стабилитрон Д818Е хорошо работает довольно в узком диапазоне токов: не менее 5 и не более 15 мА. Напряжение стабилизации стабилитрона равно 9 В, поэтому оно подается на делитель, составленный из большего постоянного (R1) и меньшего подстроечного (R2) резистора «под отвертку», с движка которого и снимается напряжение, равное 1 В.

Вместо всей этой конструкции, конечно, можно поставить небольшую микросхему – источник опорного напряжения или просто любой стабилизатор из серии LM, только сопротивление R1 придется пересчитать так, чтобы в среднем положении движка R2 на нем сохранилось около 1 В. Потенциометром этим можно плавно менять всю шкалу напряжений на выходе (но до определенного предела, ограниченного как снизу, так и сверху). Разумеется, эту цепочку вполне можно заменить двумя постоянными резисторами.

Теперь перейдем к транзистору VT3 вкупе с резистором R3. Эта простая и остроумная конструкция выполняет важнейшую функцию – она ограничивает выходной ток. Как это происходит? Обратите внимание, что весь выходной ток протекает через резистор R3, номинальное значение которого всего 0,3 Ом. В нормальном состоянии (например, на холостом ходу) падение напряжения на этом резисторе мало, поэтому транзистор VT3 закрыт, и весь этот фрагмент не оказывает никакого влияния на работу схемы. Когда же выходной ток достигает значения примерно 2 А, падение напряжения на нем достигает сакраментальных 0,6 В, транзистор VT3 приоткрывается и начинает шунтировать переход база‑эмиттер силового транзистора VT2, призакрывая его. В результате схема приходит в равновесие – если бы VT3 приоткрылся еще больше, закрывая силовой транзистор, выходной ток бы упал, падение напряжения на R3 бы уменьшилось, VT3 бы призакрылся, ну и т. д. – и все застывает на уровне 2 А выходного тока, даже при коротком замыкании на выходе! Как только избыточная нагрузка на выходе будет снята, схема автоматически вернется в нормальный режим. Если вместо резистора R3 поставить переключатель с набором сопротивлений, то можно регулировать уровень стабилизации выходного тока. Так, набор резисторов 0,3; 0,6; 1,2; 2,4; 6 и 62 Ом дадут ряд ограничений тока на уровне 2; 1; 0,5, 0,25 А, 100 и 10 мА.

Кстати, к следящему транзистору VT3 никаких требований не предъявляется – т. е., вообще никаких – можно взять любой кремниевый транзистор, только он должен быть маломощным (чтобы не шунтировать силовой транзистор токами утечки) и не составным по схеме Дарлингтона. А вот силовой транзистор, наоборот, должен быть именно дарлингтоновский, с «супербетой».

В этой схеме есть одно, однако большое НО. Заключается оно в том, что при коротком замыкании на выходе все напряжение питания будет падать на переходе коллектор‑эмиттер транзистора VT2 – ему больше просто некуда деваться. То есть, выделяющаяся мощность на VT2 составит аж целых 40 Вт! И в нормальном режиме при маленьких установленных выходных напряжениях (3 или 5 В) и максимальной нагрузке эта мощность будет практически такой же. В этом и заключается главный недостаток рассматриваемой схемы, общий для всех линейных стабилизаторов – крайне низкий КПД.

Есть, впрочем, немало способов этот КПД повысить. Продаю идею простейшего из них, который годится именно для стабилизатора с дискретным набором выходных напряжений: надо взять трансформатор нестабилизированного источника, от которого питается вся эта схема, с несколькими обмотками на разное напряжение, а к переключателю делителя добавить еще одно направление переключения так, чтобы при снижении напряжения на выходе напряжение питания стабилизатора также снижалось (с учетом того, что минимальный перепад между входом и выходом здесь должен составить не менее 4–5 В, а если используется стабилитрон, как на рис. 9.12, то напряжение на входе должно быть не меньше 12 В). Есть и более изощренные способы – скажем, регулировать действующее значение выпрямленного пульсирующего напряжения перед фильтром с помощью тиристорного моста. Но в таком случае схема настолько усложняется, что проще просто взять и построить импульсный источник.

И, наконец, несколько слов про основного нашего героя – операционный усилитель. Здесь указан классический ОУ типа μА741, который выпускается уже много десятков лет, и приведена нумерация выводов (цоколевка) для него. У него есть и отечественный аналог – КР140УД7 (учтите на будущее, что отечественные аналоги западных микросхем не всегда имеют ту же цоколевку, так что это на всякий случай надо проверять). Вообще же можно взять почти любой ОУ широкого применения с надлежащим допустимым питанием – но эти подробности мы будем рассматривать уже в главе 12 .

В заключение этой темы – еще два слова о регулируемом двухполярном лабораторном источнике. Нет никакого смысла изобретать его специально – надо просто взять два одинаковых однополярных источника, разместить их в одном корпусе (и даже запитать их от одного трансформатора, но обязательно от разных вторичных обмоток), и вывести наружу все четыре выходные клеммы по отдельности. Соединяя «плюс» одного источника с «минусом» другого перемычкой, вы получаете общую «землю» двухполярного источника, убирая перемычку – имеете два раздельных однополярных.

Рассеивание тепла

Сразу скажем – теоретической методики для расчета охлаждающих радиаторов не существует. По этому поводу можно написать не одну диссертацию или монографию (и написаны, и много), но стоит изменить конфигурацию охлаждающих ребер или стержней, расположить радиатор не вертикально, а горизонтально, приблизить к нему любую другую поверхность снизу, сверху или сбоку – все изменится, и иногда кардинально. Именно поэтому производители микропроцессоров или процессоров для видеокарт предпочитают не рисковать, а снабжать свои изделия радиаторами с вентилятором – принудительный обдув, даже слабенький, повышает эффективность теплоотвода в десятки раз, хотя нередко это совершенно не требуется (но они поступают по закону «лучше перебдеть, чем недобдеть», и это правильно). Здесь мы приведем только пару эмпирических способов, которые оправдали себя на практике и годятся для того, чтобы рассчитывать пассивные (т. е. без обдува) радиаторы для усилителя из главы 8 или для линейных источников питания из этой главы.

Сначала посмотрим, как рассчитывать площадь радиаторов, исходя из их геометрии. На рис. 9.14 схематично показан типичный пластинчатый радиатор.

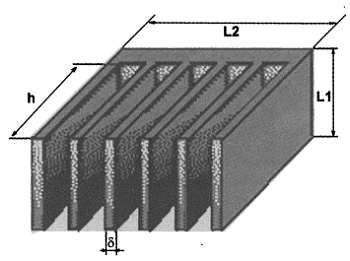
Рис. 9.14. Типичный пластинчатый радиатор

Для расчета его площади нужно к площади его основания прибавить суммарную площадь его ребер (также с каждой стороны). Если нижней стороной радиатор прижимается к плате, то лучше считать рабочей только одну сторону основания, но мы предположим, что радиатор «висит в воздухе» (как часто и бывает) и поэтому площадь основания удваивается: S_осн = 2L₁ · L₂ . Площадь одного ребра (тоже с двух сторон): S_р = 2·L₁ ·h , но к этой величине нужно еще прибавить боковые поверхности ребра, площадь которых равна S_бок = 2·h ·δ . Ребер всего 6, поэтому общая площадь радиатора равна: S = S_осн + 6·S_р + 6·S_бок . Пусть L₁ = 3 см, L₂ = 5 см, h = 3 см, S = 0,2 см, тогда общая площадь такого радиатора 145 см². Разумеется, это приближенный расчет (мы не учли, скажем, боковую поверхность основания), но для наших целей высокая точность и не требуется.

Вот два эмпирических способа для расчета рассеиваемой мощности в зависимости от площади поверхности, и пусть меня не слишком строго осудят за то, что никаких особенных научных выкладок вы здесь не увидите.

Способ первый и наипростейший – площадь охлаждающего радиатора должна составлять 10 см² на каждый ватт выделяющейся мощности. Так что радиатор с приведенными на рис. 9.14 размерами, согласно этому правилу, может рассеять 14,5 Вт мощности – как раз под наш усилитель с некоторым запасом. И если вас не жмут размеры корпуса, то вы вполне можете ограничиться этим прикидочным расчетом.

Если же хотите подсчитать поточнее, то вот один из более сложных способов, который годится для радиаторов средних размеров (L₁ = 20‑180 мм, L₂ = 40‑125 мм).

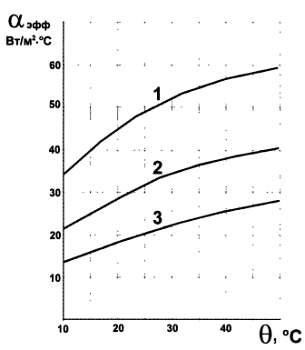
Рис. 9.15. Эффективный коэффициент теплоотдачи ребристого радиатора в условиях свободной конвекции при различной длине ребра:

1 – h = 32 мм; 2 – h = 20 мм; 3 – h = 12,5 мм

Для оценки тепловой мощности радиатора можно использовать формулу

W = α_эфф ·θ ·S , где:

□ W – мощность, рассеиваемая радиатором, Вт;

□ α_эфф – эффективный коэффициент теплоотдачи, Вт/м²·°С (см. график на рис. 9.15);

□ θ – величина перегрева теплоотдающей поверхности, °С, θ = Т_с – Т _{о с} (Т_с – средняя температура поверхности радиатора, Т_ос – температура окружающей среды);

□ S – полная площадь теплоотдающей поверхности радиатора, м².

Обратите внимание, что площадь в эту формулу подставляется в квадратных метрах, а не сантиметрах.

Итак, приступим: сначала зададимся желательным перегревом поверхности, выбрав не слишком большую величину, равную 30 °C. Грубо говоря, можно считать, что при температуре окружающей среды 30 °C, температура поверхности радиатора составит 60 °C. Если учесть, что разница между температурой радиатора и температурой кристалла транзистора или микросхемы при хорошем тепловом контакте (о котором далее) может составить примерно 5 °C, то это приемлемо для практически всех полупроводниковых приборов. Высота ребер h у нас составляет 30 мм, поэтому смотрим на верхнюю кривую из графика на рис. 9.15, откуда узнаем, что величина коэффициента теплоотдачи составит примерно 50 Вт/м²·°С. После вычислений получим, что W = 22 Вт. По простейшему правилу ранее мы получили 14,5 Вт, а сейчас, проведя более точные расчеты, мы можем несколько уменьшить площадь, тем самым сэкономив место в корпусе. Однако повторим, если место нас не жмет, то лучше всегда иметь запас.

Радиатор следует располагать вертикально, и ребра также должны располагаться вертикально (как на рисунке), а поверхность его нужно покрасить в черный цвет.

Я еще раз хочу напомнить, что все эти расчеты очень приблизительны, и даже сама методика может измениться, если вы поставите радиатор не вертикально, а горизонтально, или ребра у него будут игольчатые вместо пластинчатых. К тому же мы никак не учитываем здесь тепловое сопротивление переходов кристалл‑корпус и корпус‑радиатор (просто предположив, что разница температур составит 5 °C). Тем не менее, указанные методы дают хорошее приближение к истине, но если мы не обеспечим хороший тепловой контакт, все наши расчеты могут пойти насмарку. Просто плотно прижать винтом транзистор к радиатору, конечно, можно, но эффективно это будет только в том случае, если поверхность радиатора в месте прижима идеально плоская и хорошо отшлифована. Практически так никогда не бывает, поэтому радиатор в месте прижима покрывают специальной теплопроводящей пастой. Ее можно купить в магазинах, а иногда тюбик с такой пастой прикладывают к «кулерам» для микропроцессоров. Наносить пасту надо тонким, но равномерным слоем, не перебарщивать в количестве. Если на один радиатор ставятся два прибора, у которых коллекторы находятся под разным напряжением[12], то под корпус нужно проложить изолирующую прокладку, под крепежные винты – изолирующие пластиковые шайбы, а на сами винты надеть отрезок изолирующей кембриковой трубки длиной, равной толщине радиатора в месте отверстия (рис. 9.16).

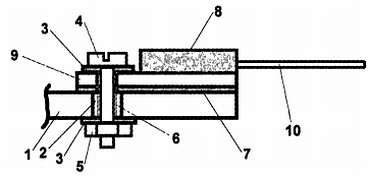
Рис. 9.16. Крепление транзистора в корпусе ТО‑220 к радиатору при необходимости его изоляции:

_{1 – радиатор;2 – отверстие в радиаторе; 3 – изолирующие шайбы; 4 – стягивающий винт; 5 – гайка; 6 – изолирующая трубка; 7 – слюдяная прокладка;8 – пластмассовая часть корпуса транзистора; 9 – металлическая часть корпуса транзистора; 10 – выводы транзистора}

Самые удобные изолирующие прокладки – слюдяные, очень хороши прокладки из анодированного алюминия (но за ними надо внимательно следить, чтобы не процарапать тонкий слой изолирующего окисла) и из керамики (которые, впрочем, довольно хрупки и могут треснуть при слишком сильном нажиме). Кстати, за неимением фирменных прокладок можно использовать тонкую фторопластовую (но не полиэтиленовую, разумеется!) пленку, следя за тем, чтобы ее не прорвать. При установке на прокладку теплопроводящая паста наносится тонким слоем на обе поверхности: и на транзистор, и на радиатор.

Принудительное охлаждение и элементы Пельтье

Тема принудительного охлаждения слишком обширна, чтобы ее можно было сколько‑нибудь подробно осветить в этой книге – тем более, что в радиолюбительской практике интенсивное охлаждение требуется редко. Потому мы опустим темы про обдув, про использование тепловых трубок и прочую экзотику, остановимся кратко лишь на применении элементов Пельтье. Эта тема заслуживает нашего внимания хотя бы просто как иллюстрация к принципу действия одного из самых интересных электронных приборов. Кстати, элементы Пельтье могут использоваться не только для охлаждения, но и для подогрева (простым изменением направления тока), т. е. с их помощью можно построить идеальный термостат, пригодный для любых условий внешней среды. И, что самое интересное, – они пригодны для выработки электроэнергии в небольших количествах, о чем несколько слов далее.

Эффект поглощения и выделения тепла в контакте из разнородных металлов при прохождении электрического тока был открыт в 1834 году французским часовщиком Жаном Пельтье. Интересно, что противоположный эффект (Зеебека, возникновения ЭДС в замкнутой цепи при контакте разнородных металлов, находящихся при различных температурах) был открыт на 13 лет раньше, но тогда еще физики не знали, что любой подобный эффект обратим, и предсказать эффект Пельтье не смогли. Как это было почти со всеми такими физическими явлениями (тензоэффект, пьезоэффект), вторую жизнь эффект Пельтье обрел с появлением полупроводников, где он проявляется гораздо сильнее. Современные элементы Пельтье изготавливаются из теллурида висмута с дозированными присадками селена и сурьмы.

Для того, чтобы правильно применять элементы Пельтье в системах охлаждения (или, неважно, подогрева), надо хорошо представлять себе, как они работают и каковы их ключевые характеристики. Потому давайте для начала проведем небольшой ликбез на эту тему.

Для тепловых насосов (к которым относится и домашний холодильник, и элемент Пельтье) понятие КПД неприменимо – отношение полезной работы к затраченной для них зависит от условий работы. Если кому будет понятней, можно провести такую аналогию – возьмите АА‑батарейку и замкните контакты накоротко. Какой КПД у батарейки в таких экстремальных условиях? Очевидно, он равен нулю – потенциалы контактов равны, вся энергия расходуется на подогрев самой батарейки. Будет он равен нулю и в противоположном случае – когда батарейка просто лежит на столе, и тока в цепи нет (ну, или почти нет – какая‑то часть энергии всегда уходит на саморазряд).

Для элементов Пельтье картина аналогичная, только в роли напряжения на контактах выступает разность температур, а в роли тока – количество переданного тепла. Если замкнуть между собой пластины элемента массивным куском меди, то разница температур будет равна нулю, а количество поглощаемого тепла – максимально. Это максимальное количество тепла (максимальная холодопроизводительность ) обозначается Q_мaкс и служит одной из характеристик элемента. Если сделать наоборот – максимально изолировать пластины друг от друга и от внешней среды (например, поместив их в безвоздушное пространство), то количество переданного тепла будет равно нулю, а разность температур максимальна. Эта величина – тоже одна из главных характеристик элемента, и обозначается Т_макс .

Типичный график в координатах температура‑холодопроизводительность для реального элемента Пельтье размером 40x40 мм, поступающего в продажу под названием FROST‑72, показан на рис. 9.17. Там же приведены максимальные значения электрических параметров этого элемента (для которых составлен верхний график). Как показывает нижняя линия, при меньших величинах напряжения питания прямая сдвинется вниз, т. е. тепловые показатели упадут. Из этих параметров можно подсчитать максимальную эффективность элемента (не путать с холодильным коэффициентом и, тем более, с КПД[13]): потребляемая электрическая мощность составит 16,3x6,2 ~= 100 ватт, т. е. максимальная эффективность будет численно равна максимальной холодопроизводительности и составит 62 %.

Из этих данных легко рассчитать охладитель с элементом Пельтье, скажем, для компьютерного процессора. Если процессор в максимуме производительности выделяет, например, 50 ватт тепла, то единичный элемент типа FROST‑72 с ним просто не справится, – при 12 вольтах питания он окажется близок к нулевому перепаду температур. В этом случае придется ставить два элемента, причем если их поставить параллельно рядом (теплораспределительная прокладка должна быть очень хорошей!), то на два следует умножать максимальное количество тепла, а если последовательно друг над другом, то удвоится максимальный перепад температур.

Построив соответствующую прямую аналогично рис. 9.17, можно прикинуть, в каком режиме будут работать элементы и какой перепад температур они примерно обеспечат.

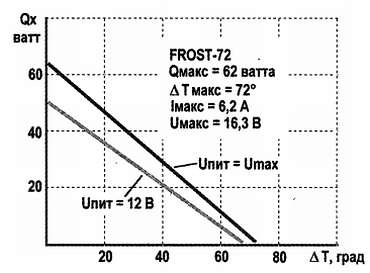
Рис. 9.17. Зависимость холодопроизводительности Q_x от разности температур пластин для элемента FROST‑72

При этом стоит учитывать, что ошибиться в холодную сторону тоже не слишком хорошо – вспомните, что современные процессоры могут самостоятельно менять потребление в зависимости от нагрузки. И если вы рассчитали элемент на перепад температур, допустим, в 40 градусов при 40 ваттах отводимого тепла, то при снижении до 10 ватт температура у вас запросто залезет в минусовые значения. Кстати, это и необязательно – точка росы при среднемосковской влажности летом на улице в 70 % достигается уже при 12° тепла. И вы имеете большой шанс залить материнскую плату конденсатом из воздуха в совершенно нормальном режиме работы. Потому обязательным компонентом охлаждающей системы с элементом Пельтье будет отдельный контроллер, который следит за температурой и регулирует мощность, подводимую к элементу, – т. е. даже в таком простейшем случае мы приходим к конструкции термостата.

Заставить элемент Пельтье вырабатывать электричество теоретически тоже несложно – для этого надо обеспечить нужный перепад температур (как можно больший и как можно более стабильный). На практике это условие, однако, может вырасти в серьезную проблему. Эксперименты показывают, что реальная выходная мощность, которую можно получить от подобной конструкции незапредельных габаритов и стоимости, составляет несколько ватт. Так что ноутбук запитать таким образом не получится, а вот подзарядить мобильник вполне реально.