Параметрический метод

Параметрический метод − это исследование системы управления, основанный на количественном выражении исследуемых свойств системы управления и установлении взаимосвязей между параметрами управляющей и управляемой подсистем. Это дает возможность на базе фактических данных определить форму зависимостей взаимосвязанных параметров, их количественное выражение.

Зависимости могут быть функциональными и корреляционными.

Функциональными называются зависимости, проявляющиеся определенно и точно в каждом отдельном случае (наблюдении). Такая взаимосвязь называется полной.

Корреляционными (неполными) называются зависимости связанных величин, искажаемые влиянием посторонних дополнительных факторов.

Пример функциональной зависимости: выпуск и продажа товаров в условиях дефицита. Коэффициент корреляции равен 1.

Пример корреляционной зависимости может служить соотношение стажа рабочего и производительности труда. Известно, что в среднем производительность труда рабочий тем выше, чем больше их стаж. Однако нередко молодой рабочий трудится лучше пожилого из-за влияния таких дополнительных факторов, как образование, здоровье и др. Чем больше влияние дополнительных факторов, менее тесна связь между стажем и выработкой. Коэффициент корреляции между стажем и производительностью занимает промежуточное положение в интервале от 0 до 1 в зависимости от тесноты взаимосвязей.

Корреляционные зависимости определяются на основе корреляционного метода.

Корреляционный (взаимосвязанный) метод − один из экономико-математических методов исследования, позволяющий определить количественную взаимосвязь между несколькими параметрами исследуемой системы. При этом корреляционная зависимость, в отличие от функциональной, может проявляться только в общем среднем случае, то есть в массе случаев – наблюдений.

Корреляционный метод применяется в теории производственных функций, в разработке разного рода нормативов на производстве, в анализе спроса и потребления и др.

Основные задачи корреляционного метода:

1) определение вида корреляционного уравнения (уравнения регрессии). Простейшим видом такого уравнения, характеризующим взаимосвязь между двумя параметрами, может быть уравнение прямой:

,

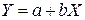где Y,X −соответственнонезависимая и зависимая переменные;

a,b −постоянные коэффициенты

Вывод о прямолинейном характере зависимости можно проверить путем простого сопоставления имеющихся данных или графически.

2) определение постоянных коэффициентов связи между переменными параметрами, которые наилучшим образом будут отвечать имеющимся фактическим значениям Y и X. В данном случае в качестве критериев оценки адекватности линейной зависимости фактическим данным можно использовать минимум суммы квадратов отклонений реальных статистических значений Y от рассчитанных по уравнению принятой к применению прямой. Коэффициенты прямой при использовании данного критерия могут быть определены известным методом наименьших квадратов.

Примером линейной зависимости можно признать количество заместителей начальника цеха Y функционального отдела от числа работников Х в отделе и на основе статистических данных (для данного примера, не менее 20-25 пар) получить следующую зависимость:

.

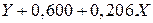Величина исследуемого параметра довольно часто складывается под влиянием не одного, а нескольких факторов. При линейной связи всех факторов можно использовать линейное уравнение множественной корреляции следующего вида:

,

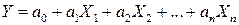где 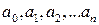− коэффициенты, рассчитанные эмпирическим путем;

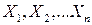− факторы, от которых зависит потребность в специалистах данного профиля. Номенклатура и количество факторов различны по категориям специалистов

Таким уравнением описывается, например, модель для функциональных специалистов.

Если же воздействие какого-либо фактора на исследуемый объект не может быть признано линейным, то соответствующие факторы могут включаться в уравнение не первой, а второй и более высокой степени.

Регрессивный анализ применяется в частности, при анализе эластичности спроса от цены, при анализе хозяйственной деятельности предприятий (для определения влияния отдельных факторов на результаты).

Факторный анализ

При анализе характеристик систем управления исследователь сталкивается с многомерностью их описания, то есть с необходимостью учитывать в анализе большое число признаков. Многие признаки взаимосвязаны и в значительной мере дублируют друг друга. Нередко признаков в косвенной форме отражают наиболее существенные, но не поддающиеся непосредственному наблюдению и измерению внутренние, скрытые свойства явлений. Поэтому возникает потребность сконцентрировать информацию, выражая большое число исходных косвенных признаков через меньшее число емких внутренних характеристик явления.

Сущность методов факторного анализа состоит в переходе от описания некоторого множества изучаемых объектов, заданного большим набором косвенных непосредственно измеряемых признаков, к описанию меньшим числом максимально информативных глубинных переменных, отражающих наиболее существенные свойства явления. Такого рода переменные, называемые факторами, являются некоторыми функциями исходных признаков.

Основная задача факторного анализа заключается в том, чтобы определить понятие, число и природу наиболее существенных характеристик (факторов).

Переменные при использовании факторного анализа не подразделяются априорно на зависимые и независимые, а рассматриваются как равноправные. Преимуществом метода является возможность одновременного исследования сколь угодно большого числа взаимосвязанных переменных. Отсутствует допущение о «неизменности всех прочих условий», свойственного многим другим методам статистического анализа. Отсутствие ограничений на число переменных и их взаимозависимость позволяет с успехом применять факторный анализ для исследования систем управления, где трудно изолировать влияние отдельных переменных на поведение всей системы.