Оптимальное решение игры двух лиц с нулевой суммой. решение матричных игр со смешанными стратегиями.
Игры с нулевой суммой — особая разновидность игр с постоянной суммой, то есть таких, где игроки не могут увеличить или уменьшить имеющиеся ресурсы, или фонд игры. В этом случае сумма всех выигрышей равна сумме всех проигрышей при любом ходе. Посмотрите направо — числа означают платежи игрокам — и их сумма в каждой клетке равна нулю. Примерами таких игр может служить покер, где один выигрывает все ставки других; реверси, где захватываются фишки противника; либо банальное воровство.
Антагонистическая игра (игра с нулевой суммой, англ. zero-sum) — термин теории игр. Антагонистической игрой называется некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.
Формально антагонистическая игра может быть представлена тройкой <X, Y, F>, где X и Y — множества стратегий первого и второго игроков, соответственно; F — функция выигрыша первого игрока, ставящая в соответствие каждой паре стратегий (ситуации) (x,y), 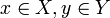 действительное число, соответствующее полезности первого игрока при реализации данной ситуации. Так как интересы игроков противоположны, функция F одновременно представляет и проигрыш второго игрока.
действительное число, соответствующее полезности первого игрока при реализации данной ситуации. Так как интересы игроков противоположны, функция F одновременно представляет и проигрыш второго игрока.
Исторически антагонистические игры являются первым классом математических моделей теории игр, при помощи которых описывались азартные игры. Считается, что благодаря этому предмету исследования теория игр и получила свое название. В настоящее время антагонистические игры рассматриваются как часть более широкого класса некооперативных игр.
Пример
| X \ Y | Орел | Решка |
| Орел | -1, 1 | 1, -1 |
| Решка | 1, -1 | -1, 1 |
Простейшим примером антагонистической игры является игра «Орлянка». Первый игрок прячет монету орлом или решкой вверх, а второй пытается угадать, как она спрятана. Если он не угадывает — он платит первому одну денежную единицу, если угадывает — первый платит ему одну денежную единицу.
В данной игре каждый участник имеет две стратегии: «орел» и «решка». Множество ситуаций в игре состоит из четырех элементов. В строках таблицы указаны стратегии первого игрока х, в столбцах — стратегии второго игрока y. Для каждой из ситуаций указаны выигрыши первого и второго игроков.
В аналитическом виде функция выигрыша первого игрока имеет следующую форму:
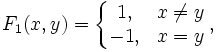
где x ∈ X и y ∈ Y — стратегии первого и второго игроков, соответственно.
Так как выигрыш первого игрока равен проигрышу второго, то F2(x,y) = − F1(x,y).
Если результат полностью определяется игроком, совершившим последний ход (если правила хода идентичны для игроков), стратегия может быть найдена с помощью функции Гранди.
Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Графический метод применим для решения игр, в которых хоть один игрок имеет две чистые стратегии. Этот метод интересен в том плане, что графически объясняет понятие седловой точки. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.
Графическое решение игр. Рассмотрим игру 2 х n, в которой игрок А имеет две стратегии.
| Таблица 1. Игра 2 х n | ||||
| . | y1: B1 | y2: B2 | ... | yn: B4 |
| x1: A1 | a11 | a12 | ... | a1n |
| 1-x1: A2 | a21 | a22 | ... | a2n |
Игра предполагает, что игрок А смешивает стратегии А1 и А2 с соответствующими вероятностями x1 и 1 - x1, 0 < x1< 1. Игрок Б смешивает стратегии B1, B2, ..., BN с вероятностями y1, y2, ..., yn, где y1 ≥ 0, j = 1, 2, ..., n, и y1 + y2 + ... + yn = 1. В этом случае ожидаемый выигрыш игрока А, соответствующий j-й чистой стратегии игрока В, вычисляется в виде (a1j - a2j)x1 - a2j, j = 1, 2, ..., n.
Следовательно, игрок А ищет величину xi, которая максимизирует минимум ожидаемых выигрышей
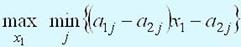
На следующем шаге мы рассмотрим применение матричных игр в смешанных стратегиях.
Рассмотрим следующую игру 2x4, в которой платежи выплачиваются игроку A.

Игра не имеет решения в чистых стратегиях, и, следовательно, стратегии должны быть смешанными. Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, приведены в следующей таблице.
| Таблица 1. Ожидаемые выигрыши игрока А | |
| Чистые стратегии игрока B | Ожидаемые выигрыши игрока А |
| -2x1 + 4 | |
| -x1 + 3 | |
| x1 + 2 | |
| -7x1 + 6 |
На рис. 1 изображены четыре прямые линии, соответствующие чистым стратегиям игрока В. Чтобы определить наилучший результат из наихудших, построена нижняя огибающая четырех указанных прямых (изображенная на рисунке толстыми линейными сегментами), которая представляет минимальный (наихудший) выигрыш для игрока А независимо от того, что делает игрок В. Максимум (наилучшее) нижней огибающей соответствует максиминному решению в точкеx1 = 0,5 . Эта точка определяется пересечением прямых 3 и 4. Следовательно, оптимальным решением для игрока Аявляется смешивание стратегий A1 и A2 с вероятностями 0,5 и 0,5 соответственно. Соответствующая цена игры vопределяется подстановкой x1 = 0,5 в уравнение либо прямой 3, либо 4, что приводит к следующему.

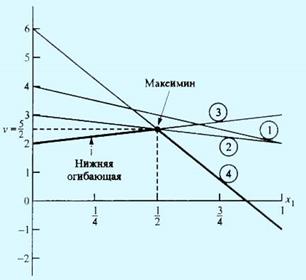
Рис. 1. Графическое решение игры двух лиц с нулевой суммой
Оптимальная смешанная стратегия игрока В определяется двумя стратегиями, которые формируют нижнюю огибающую графика. Это значит, что игрок В может смешивать стратегии B3 и B4, в этом случае y1 = y2 = 0 и y4 = y3. Следовательно, ожидаемые платежи игрока В, соответствующие чистым стратегиям игрока А, имеют такой вид
| Таблица 1. Ожидаемые выигрыши игрока А | |
| Чистые стратегии игрока A | Ожидаемые платежи игрока B |
| -4y3 - 1 | |
| -4y3 + 6 |
Наилучшее решение из наихудших для игрока В представляет собой точку минимума верхней огибающей заданных двух прямых (построение прямых и определение верхней огибающей будет для вас поучительным). Эта процедура эквивалентна решению уравнения
4y3 - 1 = -4y3 + 6
Его решением будету y3 = 7/8, что определяет цену игры v = 4 х (7/8) - 1 = 5/2.
Таким образом, решением игры для игрока А является смешивание стратегий A1 и A2 с равными вероятностями 0,5 и 0,5, а для игрока В — смешивание стратегий B3 и B4, с вероятностями 7/8 и 1/8. (В действительности игра имеет альтернативное решение для игрока В, так как максиминная точка на рис. 1 определяется более чем двумя прямыми. Любая выпуклая линейная комбинация этих альтернативных решений также является решением задачи.)
Для игры, в которой игрок А имеет m стратегий, а игрок В — только две, решение находится аналогично. Главное отличие состоит в том, что здесь строятся графики функций, представляющих ожидаемые платежи второго игрока, соответствующие чистым стратегиям игрока А. В результате ведется поиск минимаксной точки верхней огибающей построенных прямых.
Билет №10
Дата добавления: 2016-05-11; просмотров: 4432;
