Итерационные методы расчета
Решение нелинейного уравнения (системы нелинейных уравнений), описывающего (описывающих) состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится следующим образом: на основе первой, достаточно грубой, оценки определяется начальное значение корня (корней), после чего производится уточнение по выбранному алгоритму до вхождения в область заданной погрешности.
Наиболее широкое применение в электротехнике для численного расчета нелинейных резистивных цепей получили метод простой итерации и метод Ньютона-Рафсона, основные сведения о которых приведены в табл. 1.
Таблица 1. Итерационные методы расчета
| Последователь-ность расчета | Геометрическая иллюстрация алгоритма | Условие сходимости итерации | Примечание |
Метод простой итерации
1.Исходное нелинейное уравнение электрической цепи 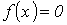 , где , где 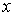 -искомая переменная, представляется в виде -искомая переменная, представляется в виде 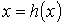 .
2. Производится расчет по алгоритму .
2. Производится расчет по алгоритму 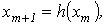 где где 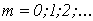 - шаг итерации.
- шаг итерации.
| 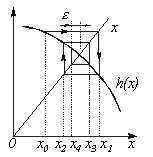 Здесь Здесь 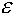 - заданная погрешность - заданная погрешность
| На интервале между приближенным и точным значениями корня должно выполняться неравенство 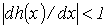
| 1.Начальное приближение 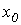 обычно находится из уравнения обычно находится из уравнения 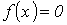 при пренебрежении в нем нелинейными членами.
2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка при пренебрежении в нем нелинейными членами.
2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка
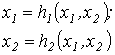 итерационные формулы имеют вид
итерационные формулы имеют вид 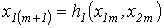 ; ;
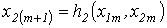 .
3. При решении системы уравнений сходимость обычно проверяется в процессе итерации. .
3. При решении системы уравнений сходимость обычно проверяется в процессе итерации.
|
Метод Ньютона-
-Рафсона
1. На основании исходного нелинейного уравнения электрической цепи 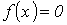 , где , где 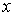 -искомая переменная, записывается итерационная формула -искомая переменная, записывается итерационная формула 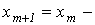 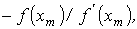 где где 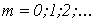 - шаг итерации.
2.По полученной формуле проводится итерационный расчет - шаг итерации.
2.По полученной формуле проводится итерационный расчет
| 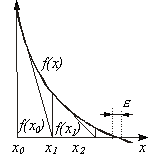 Здесь Здесь 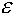 - заданная погрешность - заданная погрешность
| На интервале между приближенным и точным значениями корня должны выполняться неравенства 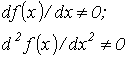
| Примечания п. 1,2 и 3 к методу простой итерации распространимы на метод Ньютона-Рафсона. При этом при решении системы 2-го порядка 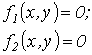 итерационные формулы имеют вид
итерационные формулы имеют вид
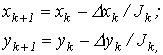 где
где
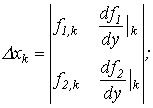 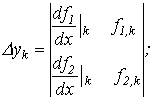
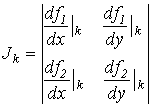
|
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.: Энергия- 1972. –200с.
- Матханов П.Н.Основы анализа электрических цепей. Нелинейные цепи.: Учеб. для студ. электротехн. спец. вузов. 2-е изд., переработ. и доп. –М.: Высш. шк., 1986. –352с.
- Чуа Л.О., Лин Пен-Мин.Машинный анализ электронных схем: алгоритмы и вычислительные методы: Пер. с англ. –М.: Энергия, 1980. – 640 с.
- Сборник задач и упражнений по теоретически основам электротехники: Учеб. пособие для вузов /Под ред. проф. П.А.Ионкина. –М.: Энергоиздат, 1982. –768 с.
Контрольные вопросы и задачи
- Как рассчитываются цепи с одним нелинейным резистором и произвольным числом линейных?
- В чем преимущества и недостатки аналитических методов расчета по сравнению с графическими?
- Какие аналитические методы используются для расчета нелинейных резистивных цепей постоянного тока?
- В чем сущность метода линеаризации? Для решения каких двух типов задач он применяется?
- Что такое эквивалентные схемы для приращений? Как они составляются?
- Какова последовательность расчета нелинейных цепей итерационными методами?
- В диагонали моста находится нелинейный резистор, ВАХ которого аппроксимирована выражением
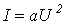 , где
, где 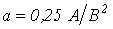 . Линейные сопротивления противоположных плеч моста попарно равны:
. Линейные сопротивления противоположных плеч моста попарно равны: 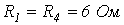 ;
; 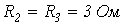 . Определить мощность, рассеиваемую нелинейным резистором, если схема питается от источника с ЭДС
. Определить мощность, рассеиваемую нелинейным резистором, если схема питается от источника с ЭДС 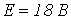 .
.
Ответ: Р=2 Вт.
- Определить ток в цепи, состоящей из последовательно соединенных линейного
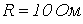 и нелинейного резисторов, если кривая ВАХ последнего
и нелинейного резисторов, если кривая ВАХ последнего 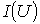 проходит через точки с координатами (15 В; 1,425 А) и (5 В; 0,325 А) и аппроксимирована выражением вида
проходит через точки с координатами (15 В; 1,425 А) и (5 В; 0,325 А) и аппроксимирована выражением вида 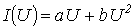 . ЭДС на входе цепи
. ЭДС на входе цепи 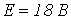 .
.
Ответ: 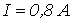 .
.
- В схеме предыдущей задачи ВАХ нелинейного резистора описывается выражением (ток – в амперах, напряжение – в вольтах)
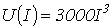 ;
; 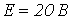 ;
; 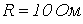 . Определить напряжение
. Определить напряжение 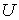 на нелинейном резисторе и ток
на нелинейном резисторе и ток 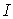 в нем методом Ньютона-Рафсона.
в нем методом Ньютона-Рафсона.
Ответ: 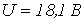 ;
; 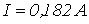 .
.
- В цепи на рис. 1,б
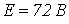 ,
, 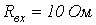 . ВАХ нелинейного резистора аппроксимирована двумя прямолинейными отрезками, первый из которых проходит через точки с координатами (0 В; 0 А) и (9 В; 2 А), а второй – через точки с координатами (9 В; 2 А) и (12 В; 6 А). Определить ток в цепи.
. ВАХ нелинейного резистора аппроксимирована двумя прямолинейными отрезками, первый из которых проходит через точки с координатами (0 В; 0 А) и (9 В; 2 А), а второй – через точки с координатами (9 В; 2 А) и (12 В; 6 А). Определить ток в цепи.
Ответ: 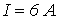 .
.
Лекция N 32
Нелинейные магнитные цепи при постоянных потоках. Основные понятия и законы магнитных цепей

При решении электротехнических задач все вещества в магнитном отношении делятся на две группы:
- ферромагнитные(относительная магнитная проницаемость
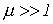 );
); - неферромагнитные(относительная магнитная проницаемость
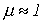 ).
).
Для концентрации магнитного поля и придания ему желаемой конфигурации отдельные части электротехнических устройств выполняются из ферромагнитных материалов. Эти части называют магнитопроводами или сердечниками.Магнитный поток создается токами, протекающими по обмоткам электротехнических устройств, реже – постоянными магнитами. Совокупность устройств, содержащих ферромагнитные тела и образующих замкнутую цепь, вдоль которой замыкаются линии магнитной индукции, называют магнитной цепью.
Магнитное поле характеризуется тремя векторными величинами, которые приведены в табл. 1.
Таблица 1. Векторные величины, характеризующие магнитное поле
| Наименование | Обозначение | Единицы измерения | Определение |
| Вектор магнитной индукции | 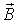
| Тл (тесла) | Векторная величина, характеризующая силовое действие магнитного поля на ток по закону Ампера |
| Вектор намагниченности | 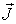
| А/м | Магнитный момент единицы объема вещества |
| Вектор напряженности магнитного поля | 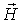
| А/м |   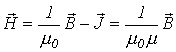 ,
где ,
где 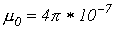  Гн/м- магнитная постоянная Гн/м- магнитная постоянная
|
Основные скалярные величины, используемые при расчете магнитных цепей, приведены в табл. 2.
Таблица 2. Основные скалярные величины, характеризующие магнитную цепь
| Наименование | Обозначение | Единица измерения | Определение |
| Магнитный поток | 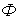
| Вб (вебер) | Поток вектора магнитной индукции через поперечное сечение 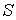 магнитопровода магнитопровода
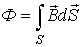
|
| Магнитодвижущая (намагничивающая) сила МДС (НС) | 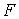
| A | 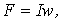 где где 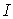 -ток в обмотке, -ток в обмотке, 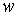 -число витков обмотки -число витков обмотки
|
| Магнитное напряжение | 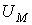
| А | Линейный интеграл от напряженности магнитного поля 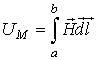 , где , где  и и 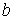 -граничные точки участка магнитной цепи, для которого определяется -граничные точки участка магнитной цепи, для которого определяется 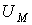
|
Дата добавления: 2017-02-04; просмотров: 803;
