Графические методы расчета
При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями.
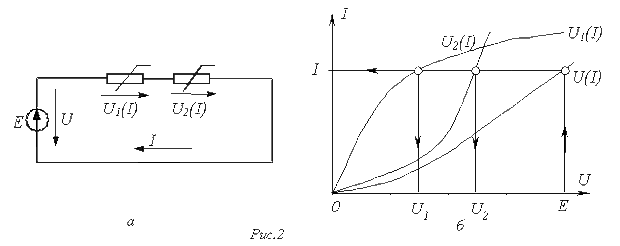
а) Цепи с последовательным соединением резистивных элементов.
При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ 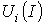 отдельных резисторов в системе декартовых координат
отдельных резисторов в системе декартовых координат  строится результирующая зависимость
строится результирующая зависимость 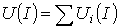 . Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью
. Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью 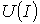 . Из точки пересечения перпендикуляра с кривой
. Из точки пересечения перпендикуляра с кривой 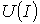 опускается ортогональ на ось токов – полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей
опускается ортогональ на ось токов – полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей 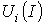 определяются напряжения
определяются напряжения 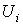 на отдельных резистивных элементах.
на отдельных резистивных элементах.
Применение указанной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис. 2,а.
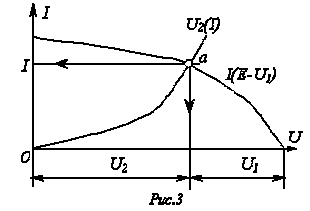 Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами может быть проведено и другим методом –методом пересечений.В этом случае один из нелинейных резисторов, например, с ВАХ
Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами может быть проведено и другим методом –методом пересечений.В этом случае один из нелинейных резисторов, например, с ВАХ 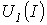 на рис.2,а, считается внутренним сопротивлением источника с ЭДС Е, а другой – нагрузкой. Тогда на основании соотношения
на рис.2,а, считается внутренним сопротивлением источника с ЭДС Е, а другой – нагрузкой. Тогда на основании соотношения 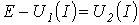 точка а (см. рис. 3) пересечения кривых
точка а (см. рис. 3) пересечения кривых 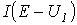 и
и  определяет режим работы цепи. Кривая
определяет режим работы цепи. Кривая 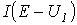 строится путем вычитания абсцисс ВАХ
строится путем вычитания абсцисс ВАХ 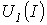 из ЭДС Е для различных значений тока.
из ЭДС Е для различных значений тока.
Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.
б) Цепи с параллельным соединением резистивных элементов.
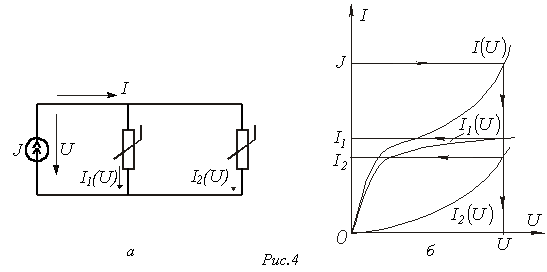
При параллельном соединении нелинейных резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам. Расчет проводится в следующей последовательности. По заданным ВАХ 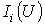 отдельных резисторов в системе декартовых координат
отдельных резисторов в системе декартовых координат  строится результирующая зависимость
строится результирующая зависимость 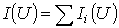 . Затем на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ
. Затем на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ 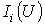 ), из которой восстанавливается перпендикуляр до пересечения с зависимостью
), из которой восстанавливается перпендикуляр до пересечения с зависимостью 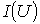 . Из точки пересечения перпендикуляра с кривой
. Из точки пересечения перпендикуляра с кривой 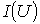 опускается ортогональ на ось напряжений – полученная точка соответствует напряжению на нелинейных резисторах, по найденному значению которого с использованием зависимостей
опускается ортогональ на ось напряжений – полученная точка соответствует напряжению на нелинейных резисторах, по найденному значению которого с использованием зависимостей 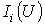 определяются токи
определяются токи  в ветвях с отдельными резистивными элементами.
в ветвях с отдельными резистивными элементами.
Использование данной методики иллюстрируют графические построения на рис. 4,б, соответствующие цепи на рис. 4,а.
в) Цепи с последовательно-параллельным (смешанным) соединением резистивных элементов.
1. Расчет таких цепей производится в следующей последовательности:
Исходная схема сводится к цепи с последовательным соединением резисторов, для чего строится результирующая ВАХ параллельно соединенных элементов, как это показано в пункте б).
2. Проводится расчет полученной схемы с последовательным соединением резистивных элементов (см. пункт а), на основании которого затем определяются токи в исходных параллельных ветвях.
Метод двух узлов
Для цепей, содержащих два узла или сводящихся к таковым, можно применять метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем:
Строятся графики зависимостей  токов во всех i-х ветвях в функции общей величины – напряжения
токов во всех i-х ветвях в функции общей величины – напряжения 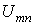 между узлами m и n, для чего каждая из исходных кривых
между узлами m и n, для чего каждая из исходных кривых 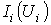 смещается вдоль оси напряжений параллельно самой себе, чтобы ее начало находилось в точке, соответствующей ЭДС
смещается вдоль оси напряжений параллельно самой себе, чтобы ее начало находилось в точке, соответствующей ЭДС 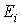 в i-й ветви, а затем зеркально отражается относительно перпендикуляра, восстановленного в этой точке.
в i-й ветви, а затем зеркально отражается относительно перпендикуляра, восстановленного в этой точке.
Определяется, в какой точке графически реализуется первый закон Кирхгофа 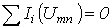 . Соответствующие данной точке токи являются решением задачи.
. Соответствующие данной точке токи являются решением задачи.
 Метод двух узлов может быть реализован и в другом варианте, отличающемся от изложенного выше меньшим числом графических построений.
Метод двух узлов может быть реализован и в другом варианте, отличающемся от изложенного выше меньшим числом графических построений.
В качестве примера рассмотрим цепь на рис. 5. Для нее выражаем напряжения на резистивных элементах в функции 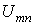 :
:
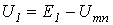 ; ;
| (1) |
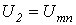 ; ;
| (2) |
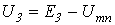 . .
| (3) |
Далее задаемся током, протекающим через один из резисторов, например во второй ветви 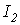 , и рассчитываем
, и рассчитываем 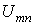 , а затем по
, а затем по 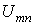 с использованием (1) и (3) находим
с использованием (1) и (3) находим 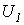 и
и 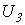 и по зависимостям
и по зависимостям  и
и 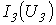 - соответствующие им токи
- соответствующие им токи 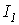 и
и 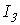 и т.д. Результаты вычислений сводим в табл. 1, в последней колонке которой определяем сумму токов
и т.д. Результаты вычислений сводим в табл. 1, в последней колонке которой определяем сумму токов
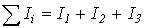 .
.
Таблица 1. Таблица результатов расчета методом двух узлов
| 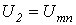
| 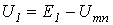
| 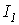
| 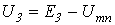
| 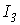
| 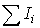
|
Алгебраическая сумма токов в соответствии с первым законом Кирхгофа должна равнять нулю, поэтому получающаяся в последней колонке табл. 1 величина 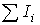 указывает, каким значением
указывает, каким значением 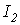 следует задаваться на следующем шаге.
следует задаваться на следующем шаге.
В осях 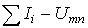 строим кривую зависимости
строим кривую зависимости 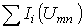 и по точке ее пересечения с осью напряжений определяем напряжение
и по точке ее пересечения с осью напряжений определяем напряжение 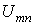 между точками m и n. Для найденного значения
между точками m и n. Для найденного значения 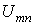 по (1)…(3) рассчитываем напряжения на резисторах, после чего по заданным зависимостям
по (1)…(3) рассчитываем напряжения на резисторах, после чего по заданным зависимостям 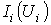 определяем токи в ветвях схемы.
определяем токи в ветвях схемы.
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.: Энергия- 1972. –200с.
Контрольные вопросы и задачи
- Почему метод наложения неприменим к нелинейным цепям?
- Какие параметры характеризуют нелинейный резистор?
- Почему статическое сопротивление всегда больше нуля, а дифференциальное и динамическое могут иметь любой знак?
- Какие методы используют для анализа нелинейных резистивных цепей постоянного тока?
- Какая последовательность расчета графическим методом нелинейной цепи с последовательным соединением резисторов?
- Какая последовательность расчета графическим методом нелинейной цепи с параллельным соединением резисторов?
- Какой алгоритм анализа цепи со смешанным соединением нелинейных резисторов?
- В чем сущность метода двух узлов?
- В цепи на рис. 2,а ВАХ нелинейных резисторов
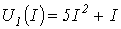 и
и  , где напряжение – в вольтах, а ток – в амперах;
, где напряжение – в вольтах, а ток – в амперах; 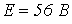 . Графическим методом определить напряжения на резисторах.
. Графическим методом определить напряжения на резисторах.
Ответ: 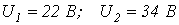 .
.
- В цепи на рис. 4,а ВАХ нелинейных резисторов
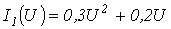 и
и 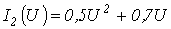 , где ток – в амперах, а напряжение – в вольтах;
, где ток – в амперах, а напряжение – в вольтах; 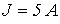 . Графическим методом определить токи
. Графическим методом определить токи 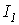 и
и 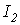 .
.
Ответ: 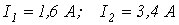 .
.
- В цепи на рис. 5
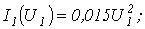
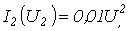 , где ток – в амперах, а напряжение – в вольтах; третий резистор линейный с
, где ток – в амперах, а напряжение – в вольтах; третий резистор линейный с 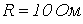 . Определить токи в ветвях методом двух узлов, если
. Определить токи в ветвях методом двух узлов, если 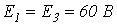 .
.
Ответ: 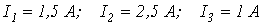 .
.
Лекция N 31
Дата добавления: 2017-02-04; просмотров: 629;
