Построение комплексных чертежей двух усеченных тел, построение разверток
Сечение – изображение фигуры, получающеёся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости.
Рассекая геометрическое тело плоскостью, получают сечение – ограниченную замкнутую линию, все точки которой принадлежат как секущей плоскости, так и поверхности тела.
Нужно обратить внимание на то, что при пересечении многогранника с плоскостью в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника, а при пересечении тел вращения фигура сечения ограничена плавной кривой линией. Точки этой кривой находят с помощью вспомогательных линий, взятых на поверхности тела (например, образующих конуса и цилиндра). Точки пересечения образующих с секущей плоскостью будут принадлежать кривой линии сечения.
Для того чтобы определить действительную величину сечений, необходимо знать способы преобразования плоскостей проекций: способ вращения и способ перемены плоскостей проекций. В качестве вспомогательных, к комплексным чертежам применяют аксонометрические проекции. Это делают в тех случаях, когда нужно дать наглядное изображение предмета.
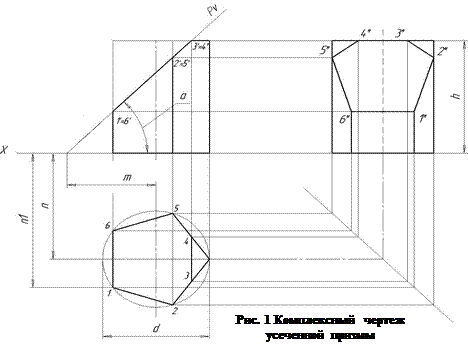 Сечение призмы плоскостью.
Сечение призмы плоскостью.
Из комплексного чертежа на рисунке 1, видно, что плоскость Рv пересекает не только боковую поверхность, но и верхнее основание призмы. Поэтому фигура сечения представляет собой плоский шестиугольник 1 2 3 4 5 6. Для построения проекций фигуры сечения находят проекции точек пересечения плоскости Рv с ребрами призмы и соединяют их прямыми линиями. Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы со следом Рv, секущей плоскости Р (точки 1` - 6`).
Горизонтальные проекции точек пересечения 1-6 совпадают с горизонтальными проекциями ребер.
Имея фронтальные и горизонтальные проекции этих точек, с помощью линий связи находят профильные проекции 1" - 6'' Полученные точки соединяют прямыми линиями и получают профильную проекцию фигуры сечения.
Сечение цилиндра плоскостью.
Построение плоского сечения прямого кругового цилиндра аналогично построению плоского сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер - образующих цилиндра.
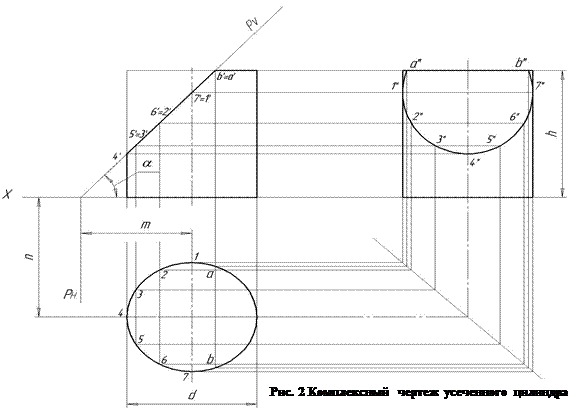 |
На рисунке 2 даны три проекции прямого кругового цилиндра, пересеченного фронтально-проецирующей плоскостью Р.
Из комплексного чертежа видно, что фронтально-проецирующая плоскость Р пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под углом к оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса.
Сечение пятигранной пирамиды плоскостью
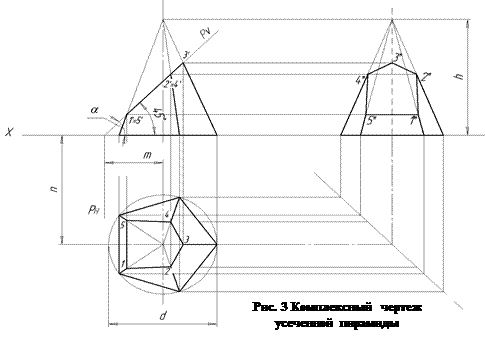 Правильная пятигранная пирамида, пересеченная фронтально-проецирующей плоскостью Р, показана на рисунке 3.
Правильная пятигранная пирамида, пересеченная фронтально-проецирующей плоскостью Р, показана на рисунке 3.
Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным следом Pv плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости Р с ребрами пирамиды.
Сечение прямого кругового конуса плоскостью.
При различном расположении секущей плоскости Р по отношению к оси прямого кругового конуса получают различные фигуры сечения, ограниченные большей частью кривыми линиями.
Сечение прямого кругового конуса фронтально-проецирующей плоскостью Р рассматривается на рисунке 4. Основание конуса расположено на горизонтальной плоскости Н. Фигура сечения в данном случае будет ограничена эллипсом.
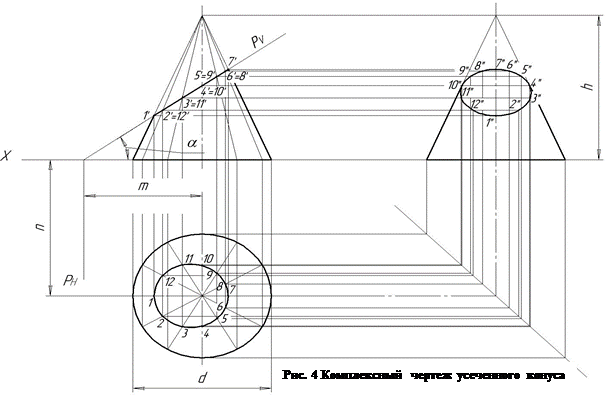 |
Для построения горизонтальной проекции контура фигуры сечения – горизонтальную проекцию основания конуса (окружность) делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях проводят вспомогательные образующие. Сначала находят фронтальные проекции точек сечения 1` - 12`, лежащих на фронтальном следе плоскости Рv. Затем с помощью линий связи находят их горизонтальные проекции. Например, горизонтальная проекция точки 2, расположенной на образующей S2, проецируется на горизонтальную проекцию этой же образующей S2 в точку 2.
Найденные горизонтальные проекции точек контура сечения соединяют по лекалу.
Построение разверток.
Развертка поверхности пирамиды с сечением.
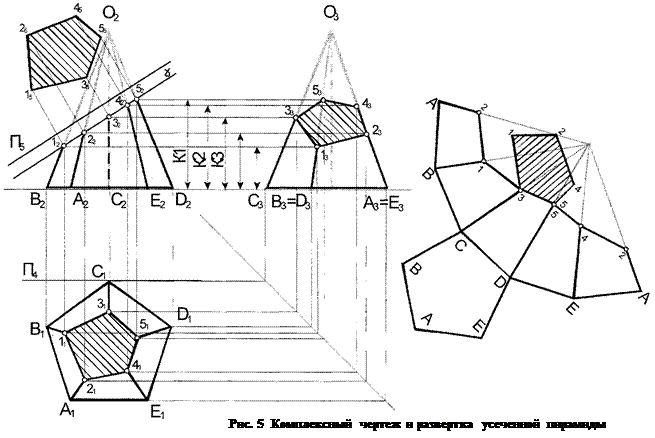
Сначала строится развертка не усеченной пирамиды все грани, которой формы треугольника, одинаковы. Намечают вершину пирамиды и из нее, как из центра, проводят дугу окружности радиусом, равным действительной длине ребра пирамиды (рис. 5). Действительную длину ребра можно определить по профильной или фронтальной проекции пирамиды. В данном примере действительная длина ребра в профильной проекции О3С3 (R), так как это ребро параллельно плоскости П3.
Далее по дуге окружности от любой точки, например А, откладываются отрезки, равные сторонам основания пирамиды (действительные длины отрезков берутся с горизонтальной проекции). Все точки основания (А, В, С, D……) соединяются с вершиной О. На каждом ребре (АО, ВО, СО, ….) откладываются соответствующие действительные длины. Действительные длины этих отрезков определяются способом вращения вокруг оси, перпендикулярной к плоскости П1, проходящей через вершину О. Для этого достаточно воспользоваться горизонтальными проецирующими лучами, между плоскостью П2 и П3. Отрезками К1, К2, К3 и т.д. Точки сечения соединить прямыми линиями.
Полученную фигуру развертки совместить с фигурой натурального сечения и основания пирамиды. Линии ребер на развертке проводят штрихпунктирной линией с двумя точками.
 |
Построение развертки усеченного цилиндра. (Рисунок 6)
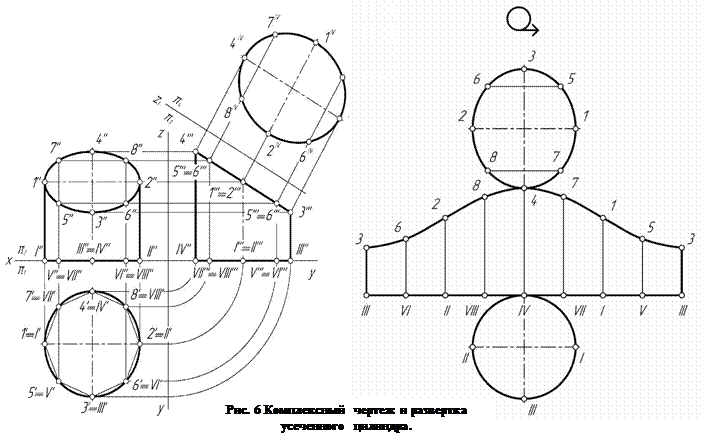 |
Рекомендуется следующая последовательность построения развертки цилиндра:
1. вписывают в цилиндр правильную восьмиугольную призму для построения приближенной развертки;
2. строят проекции сечения. Отмечают проекции точек встречи секущей плоскости с ребрами призмы. По принадлежности находят проекции этих точек на плоскостях проекций. Фигуры, образуемые точками, являются проекциями сечения (в рассматриваемом примере сечение боковой поверхности цилиндра представляет собой эллипс);
3. способом замены плоскостей проекций находят натуральную величину сечения. Новую плоскость проекций располагают параллельно выраженной проекции фигуры сечения. Проводят линии связи, перпендикулярные новой оси проекций. От новой оси по линиям связи откладывают соответствующие координаты точек.
4. строят развертку боковой поверхности. На горизонтальной прямой откладывают отрезки, равные длинам сторон основания призмы, перпендикулярно прямой проводят отрезки, равные длинам соответствующих ребер. Полученные точки соединяют;
5. к развертке боковой поверхности достраивают фигуры основания и сечения. Полученная плоская фигура есть полная развертка усеченной части цилиндра.
Построение развертки усеченной призмы
Рекомендуется следующая последовательность построения развертки призмы (рисунок 7):
1. по заданным проекциям призмы строят ее комплексный чертеж;
2. строят проекции сечения. Отмечают проекции точек встречи секущей плоскости с ребрами призмы. По принадлежности находят проекции этих точек на плоскостях проекций. Фигуры, образуемые точками, являются проекциями сечения призмы;
3. способом замены плоскостей проекций находят натуральную величину сечения. Новую плоскость проекций располагают параллельно вырожденной проекции фигуры сечения. Проводят линии связи, перпендикулярные новой оси проекций. От новой оси по линиям связи откладывают соответствующие координаты точек.
4. строят развертку боковой поверхности призмы. На горизонтальной прямой откладывают отрезки, равные длинам сторон основания призмы, перпендикулярно прямой проводят отрезки, равные длинам соответствующих ребер. Полученные точки соединяют;
5. 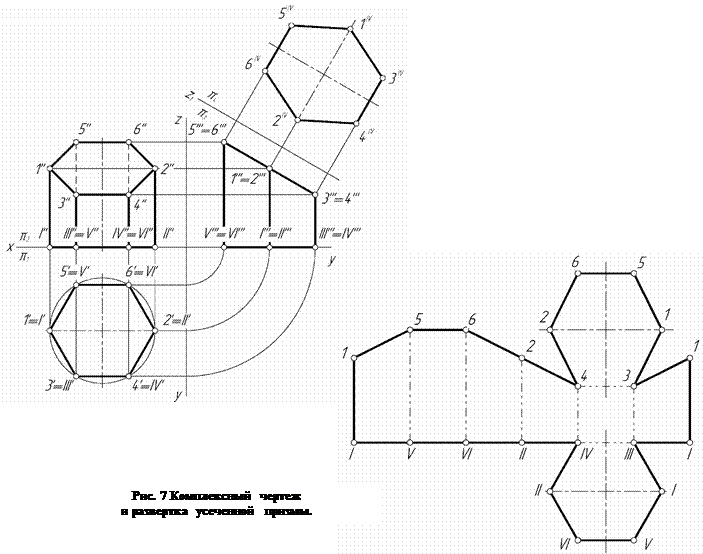 к развертке боковой поверхности достраивают фигуры основания и сечения призмы. Полученная плоская фигура есть полная развертка усеченной части призмы.
к развертке боковой поверхности достраивают фигуры основания и сечения призмы. Полученная плоская фигура есть полная развертка усеченной части призмы.
Построение развертки усеченного конуса.
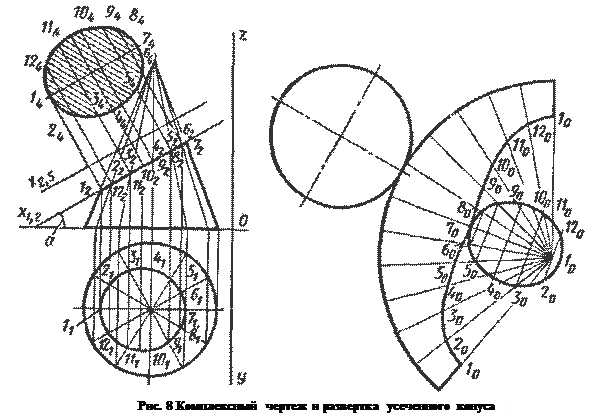
Для построения полной развертки усеченной плоскостью части прямого кругового конуса делим основание конуса на 12 равных частей и проводим через точки деления образующие. Находим точки их пересечения с плоскостью Р (рис.8). Далее строим развертку полного конуса (радиус сектора равен образующей конуса) и на каждой образующей откладываем натуральную величину отрезка соответствующей образующей усеченного конуса от его вершины до точки пересечения с плоскостью Р. Концы этих отрезков соединяем плавной кривой. Для получения полной развертки нижней части конуса необходимо добавить к развертке его боковой поверхности основание — круг и фигуру сечения — эллипс, найдя предварительно его натуральную величину
 |
Построение аксонометрии усеченных геометрических тел. (рис.9)
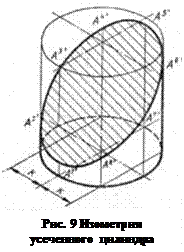 Построение аксонометрических проекций усеченных геометрических тел осуществляем в следующем порядке: строим проекции не усеченного тела, наносим на его боковую поверхность образующие, пользуясь размерами. На образующих от нижнего основания откладываем оставшиеся части образующих (размеры берем с фронтальной проекции). Соединяем между собой верхние точки A1', A2', А3'..... A8', прямыми или плавной кривой при помощи лекала и получаем аксонометрию фигуры сечения. Выявляем контур оставшейся части геометрического тела, обводим видимые и невидимые элементы соответствующими линиями и заштриховываем фигуру сечения.
Построение аксонометрических проекций усеченных геометрических тел осуществляем в следующем порядке: строим проекции не усеченного тела, наносим на его боковую поверхность образующие, пользуясь размерами. На образующих от нижнего основания откладываем оставшиеся части образующих (размеры берем с фронтальной проекции). Соединяем между собой верхние точки A1', A2', А3'..... A8', прямыми или плавной кривой при помощи лекала и получаем аксонометрию фигуры сечения. Выявляем контур оставшейся части геометрического тела, обводим видимые и невидимые элементы соответствующими линиями и заштриховываем фигуру сечения.
Практическая часть
Задание.
Часть 1. Дайте ответ на вопросы теста.
1. Какая фигура образуется в сечении треугольной призмы, если заданная плоскость пересекает два боковых ребра и треугольник основания?
| Прямоугольник | Треугольник | Четырехугольник | Шестиугольник |
2. Какая фигура образуется в сечении четырехугольной пирамиды, если заданная плоскость пересекает три боковых ребра и четырехугольник основания?
| Треугольник | Пятиугольник | Шестиугольник | Четырехугольник |
3. Какое наибольшее число ребер куба может пересечь одна плоскость?
| Четыре | Семь | Пять | Шесть |
4. Какая из плоскостей пересекает куб, образуя четырехугольник?
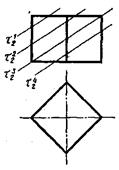 | |||
 | |||
5. Какая плоскость образует в сечении многоугольник с наибольшим числом вершин?
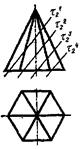 | |||
 | |||
6. Из скольких плоских фигур состоит полная развертка правильной пятиугольной призмы?
| Семи | Шести | Восьми | Пяти |
7.Из скольких плоских фигур состоит полная развертка правильной шестиугольной пирамиды?
| Восьми | Шести | Пяти | Семи |
Часть 2.В рабочей тетради, по размерам заданным в таблице, построить три проекции усеченной шестиугольной правильной пирамиды.
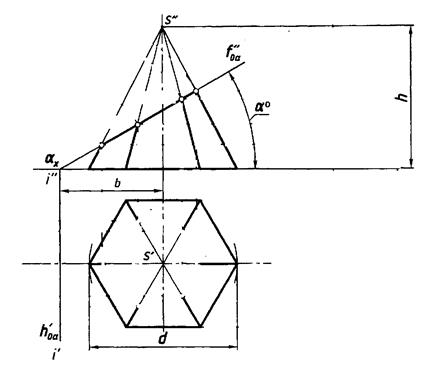 |
| Вариант | d | h | b | а° |
| 300 | ||||
| 450 | ||||
| 300 | ||||
| 450 | ||||
| 300 | ||||
| 300 | ||||
| 450 | ||||
| 300 | ||||
| 450 | ||||
| 300 | ||||
| 300 | ||||
| 300 | ||||
| 300 | ||||
| 450 | ||||
| 300 | ||||
| 450 |
| <== предыдущая лекция | | | следующая лекция ==> |
| Пример 4. Проверка теплоустойчивости ограждающей конструкции | | | Транспортный уровень |
Дата добавления: 2016-04-22; просмотров: 21413;
