Дополнительные сведения

Подчеркнем, что при выравнивании маржинальных цен достигается минимум только переменной части затрат. Полученный при таком планировании объем выпуска продукции может дать выручку, которая не окупит полные затраты.

В простейших случаях планирование выпуска товара может быть выполнено графически. На рис. 17 а) и б) приведены характеристики предложения двух производителей.

Для определения загрузки каждого из них:

· строится суммарная характеристика предложения (рис. 17 в)). Для этого характеристики отдельных производителей суммируются по оси абсцисс;

· по оси абсцисс на графике суммарной характеристики (рис. 17 в)) откладывается величина требуемого суммарного объема выпуска товара 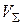. (Для примера с несколькими электростанциями - это суммарная нагрузка потребителей);

· пересечение вертикальной линии от 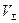с суммарной характеристикой дает значение оптимальной и одинаковой для всех производителей маржинальной цены р_М ;

· по индивидуальным характеристикам предложения ( рис. 17 а) и б)) находятся оптимальные объемы выпуска товара V₁ и V₂ . Эти объемы соответствуют единой маржинальной цене р_М и обеспечивают наименьшие суммарные издержки производства.

Б) Планирование производства разными участниками конкурентного рынка

Предположим, что в условиях рынка каждый его участник независим и обладает свободой поведения. Для участников конкурентного рынка не актуально добиваться минимума суммарных издержек всех производителей, как это рассматривалось в предыдущей задаче. Возможная цель каждого поставщика – достижение минимума собственных затрат. При этом информация об экономических характеристиках одного поставщика не известна другому.

Пусть 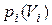- характеристика предложения i-го поставщика. Если он производит 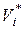количество товара, то его издержки 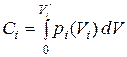. Этот поставщик стремится произвести столько товара, чтобы обеспечить минимум своих затрат С_i .

Другой поставщик тоже минимизирует свои затраты. Если они действуют не согласованно, то вместе произведут столько товара, количество которого не будет соответствовать спросу потребителей на рынке.

Поиск решения такой задачи выполняется с помощью методов многокритериальной оптимизации[2]. При этом учитывается суммарный спрос потребителей, и минимизируются издержки каждого поставщика. Для того, чтобы продать весь произведенный товар, поставщикам часто приходится «идти на уступки» и организовывать производство с затратами, бóльшими, чем их минимальное значение.

Дополнительный материал[3]

Выведенный логически закон планирования можно получить математически. Рассмотрим упрощенный пример, в котором две тепловые электростанции вырабатывают электроэнергию для снабжения одного потребителя.

Загрузка станций Р1 и Р2 . Нагрузка потребителя РН . Известны расходные характеристики станций С1(Р1) и С2(Р2). Они непрерывны и нелинейны. Потери в электрической сети не учитываются. Требуется найти оптимальную загрузку электростанций, обеспечивающую наименьшие суммарные затраты на производство электроэнергии по энергосистеме.

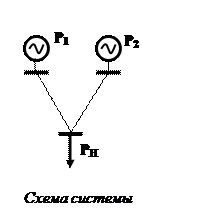
Запишем оптимизационную задачу

min [C₁(P₁)+C₂(P₂)]

при ограничении Р₁+Р₂-Р_Н=0.

Неизвестные Р₁ и Р_{2 .}

Записанная задача относится к задачам нелинейного математического программирования. Ее решение может быть найдено с использованием метода множителей Лагранжа. В рамках этого метода минимизируется функция Лагранжа

L=C₁(P₁)+C₂(P₂)+ 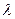(Р₁+Р₂-Р_Н),

в которой 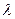- множитель Лагранжа.

Для поиска неизвестных решается система уравнений

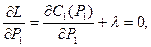
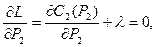
Производные 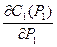и 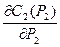показывают, как меняются издержки при малом изменении выпуска продукции (электроэнергии). Это маржинальные цены производителей (электростанций).

Из системы уравнений следует, что 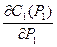= = 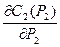- 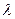минимальные суммарные издержки на выработку электроэнергии достигаются при равенстве маржинальных цен электростанций. Конец дополнительного материала.