Расчет параметров системы линейных уравнений
| T | xt | T2 | t × xt | Уt | t × уt |  t t
|  t t
|
2. Рассчитать параметры уравнения, определяющего теоретическое значение переменной X. С этой целью решить систему нормальных уравнений (1, 2):
ìåхt = n ax + bx åt (1)
í
îåxt × t = ax åt + bx åt2 (2)
3. Рассчитать теоретические значения X в ретроспективном периоде и отклонения расчетных величин от фактических
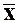 t = ax + bx * t (3)
t = ax + bx * t (3)
e t = xt - 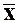 (4)
(4)
4. Рассчитать параметры уравнения, определяющего теоретическое значение переменной Y. С этой целью решить систему нормальных уравнений (5, 6):
ìåYt = n ay + by åt (5)
í
îåYt * t = ay åt + by åt2 (6)
5. Рассчитать теоретические значения Y в ретроспективном периоде и отклонения расчетных величин от фактических
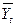 = ay + by*t ( 7 )
= ay + by*t ( 7 )
ν = Yt - 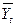 ( 8 )
( 8 )
6.
|
 |
Проверить предположение о том, что запаздывание во взаимодействии переменных равно нулю. С этой целью провести статистическую обработку информации и рассчитать коэффициент корреляции при величине временного лага ( L ) равной нулю. Создать таблицу 3.
Таблица 3
Расчет параметров уравнения регрессии (L =0)
| T | εt | νt | εt* νt | εt2 | νt2 |
7.
|
 |
Последовательно проверить гипотезы о том, что L = 1, L = 2, L =3 годам. Рассчитать коэффициенты корреляции. Создать таблицы 4 и 5. При необходимости проверки гипотезы о том, что L = 3, 4 и т.д., создать дополнительные таблицы, аналогичные таблице 4.
Таблица 4
Расчет параметров уравнения регрессии (L = 1)
| T | εt-1 | νt | εt-1* νt | εt-12 | Νt2 |
Таблица 5
Расчет параметров уравнения регрессии (L = 2)
| T | εt-2 | νt | εt-2* νt | εt-22 | νt2 |
8. При подтверждении гипотезы о запаздывании во взаимодействии переменных, сделать вывод о величине временного лага и определить параметры уравнения регрессии. Для их расчета воспользуйтесь методом исключения тенденций, который основан на замене исходных элементов динамических рядов отклонениями. Прогнозная функция может быть записана в виде (11) или (12)
νt = f (εt) (11)
νt = α*εt (12)
α - коэффициент пропорциональности, может быть определен методом наименьших квадратов из нормального уравнения (13).
∑ νt* εt = α *∑ εt2 (13)
α = 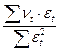 (14)
(14)
Для расчета абсолютных значений исследуемых показателей на прогнозный период в уравнении регрессии следует заменить отклонения νt и εt переменными Xt и Yt.
εt = Xt - 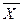 = Xt – axt – bxt *t (15)
= Xt – axt – bxt *t (15)
νt = Yt -  = Yt – ayt – byt *t (16)
= Yt – ayt – byt *t (16)
Подставив их в уравнение 12, получим уравнение 17.
Yt – ayt – byt t = (Xt – axt – bxt t )* α (17)
9. Рассчитать прогнозные значения валового сбора в 2006, 2007г.
Тема 8.
Дата добавления: 2016-04-22; просмотров: 772;
