Сущность корреляционно-регрессионного анализа

Корреляционнo-регрессионный анализ- используется для исследования форм связи, устанавливающих количественные соотношения между случайными величинами изучаемого процесса. В социально-экономическом прогнозировании этот метод применяют для построения условных прогнозов. При этом значение независимой переменной (Х) нам известно по предположению. В процессе прогнозирования оно может быть использовано нами для оценки зависимой переменной (Y). Функция регрессии Y = f(X_1, X_2, X_3, X_4,…X_m) показывает, каким будет в среднем значение переменной Y, если переменные X примут конкретное значение.

Переменная Y, характеризующая результат, формируется под воздействием других переменных и факторов. Поэтому она всегда стохастична (случайна) по природе. Переменные Х (объясняющие переменные), характеризуют причину. Они поддаются регистрации, а часть из них планированию и регулированию. Значения ряда переменных Х могут задаваться "извне" прогнозируемой системы. По своей природе объясняющие переменные могут быть случайными и неслучайными. Регрессионные остатки ε - это латентные (скрытые) случайные компоненты, влияющие на Y, а также случайные ошибки в измерении анализируемых результирующих переменных.

В зависимости от количества исследуемых переменных различают парную и множественную корреляцию.

Парная корреляция - корреляционные связи между двумя переменными. Примерами парной корреляции могут служить зависимости между уровнем образования и производительностью труда, между ценой товара и спросом на него, между качественными параметрами товара и ценой. Экономико-математические модели, построенные с учетом такого рода взаимосвязей, называют однофакторными моделями. Следует отметить, что в практике прогнозирования экономических явлений однофакторные модели занимают значительное место, что определяется простотой вычислительного процесса и ясностью экономической интерпретации результатов.

Множественная корреляция - корреляционные взаимосвязи между несколькими переменными. В качестве примеров множественной корреляции можно привести зависимость спроса на товар от цены, уровня доходов населения, расходов на рекламу; зависимость объема выпускаемой продукции от размера инвестиций, технического уровня оборудования, численности занятых в процессе производства.

Примеры корреляционных зависимостей

1.Примером использования корреляционной зависимости для прогнозирования и принятия управленческих решений могут служить кривые спроса и предложения, на основе которых строятся модели, описывающие последствия изменения цен.

2.В конце ХIХ века немецкий статистик Э. Энгель сформулировал законы и построил кривые, согласно которым с ростом дохода доля расходов на питание сокращается, доля расходов на одежду и жилище остается неизменной, а расходов на образование и лечение – увеличивается. Данные кривые послужили исходным пунктом построения различных моделей, описывающих поведение покупателей при изменении их доходов и соответственно используемых при прогнозировании спроса на товары и услуги.

3.Немецкий исследователь Г.Госсен сформулировал утверждения о зависимости потребительской оценки полезности от количества благ и дал им математическую интерпретацию.

4.Примерами множественной корреляции могут служить различные модели экономического роста (модель Е.Домара, модель Р.Ф.Харрода, модель Р.Солоу), описывающие зависимость реального дохода в экономике от наиболее значимых факторов.

5.В конце 60-х годов ХХ века эмпирическим путем была установлена закономерность снижения переменных издержек на производство единицы продукции на 10-30 % при каждом удвоении объема производства. Данная зависимость получила название кривая опыта. Она лежит в основе многих концепций деловой стратегии.

При анализе временных рядов часто встречается ложная корреляция, когда параллельно повышаются или снижаются показатели, на самом деле совершенно не зависящие друг от друга. Ложная корреляция - это отсутствие причинной связи между явлениями, связанными корреляционной связью.

Регрессионный анализ - часть теории корреляции. В процессе регрессионного анализа решаются задачи выбора независимых переменных, существенно влияющих на зависимую величину, определение формы уравнения регрессии, оценивание параметров.

Мы рассмотрим модель линейной регрессии, как наиболее доступную для понимания и довольно часто используемую на практике. Множественные модели также находят практическое применение, но обычно для их построения используются пакеты прикладных программ. Проблема, с которой сталкивается прогнозист при использовании пакетов прикладных программ, заключается в оценке адекватности отображения действительности и будущих взаимосвязей в регрессионных моделях и корректное их использование для прогнозирования будущего.

7.3. Прогнозирование на основе однофакторных моделей линейной регрессии: последовательность процедур

1. Сбор исходной информации.

2. Качественный анализ взаимосвязи исследуемых показателей, определение причинно-следственной связи между анализируемыми характеристиками.

3. Оценка тесноты связи. Расчет коэффициента корреляции.

Коэффициент корреляции (R) - характеризует тесноту связи между случайными величинами (Х, У), может быть рассчитан по формуле 40.

R_x,y= (40),

По численному значению коэффициента корреляции можно сделать следующие выводы:

R = 0 - рассматриваемые величины не взаимосвязаны;

R = 1 - имеет место прямая функциональная зависимость, изменение значений переменных однонаправленное, при увеличении одной переменной другая тоже увеличивается;

R = -1 - имеет место обратная функциональная зависимость, изменение значений переменных разнонаправленное, при увеличении одной переменной, другая уменьшается.

В практике расчетов мы можем получить значения коэффициентов близкие к одной из названных величин. По абсолютному значению коэффициента корреляции можно прийти к следующим заключениям:

0 R< 0,2 - связи практически нет,

0,2 R< 0,5 - связь слабая,

0,5 R< 0,75 - связь заметная,

0,75 R< 0,95 - связь тесная,

0,95 R 1 - связь близкая к функциональной.

На практике принято строить прогнозы на основе взаимосвязей с коэффициентом корреляции от 0,75 до 1.

Виды корреляционных зависимостей показаны на рисунке 5.

y . y .. :: ..× . y ..

× ...× . ..× . : ::× .×

. .. : : . : × : .. ...× :

. . . : . : . × . ..::: × ×..

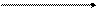х х х

1 2 3

Рис. 5. Виды корреляционных зависимостей

(1 - переменные Х и У не коррелируются; 2 - слабая положи-

тельная корреляция; 3 - сильная отрицательная корреляция)

4. Расчет параметров уравнения регрессии. Корреляционное уравнение (уравнение регрессии) - математическое описание корреляционных связей. Оценка параметров уравнения регрессии осуществляется методом наименьших квадратом на основе следующих формул (41, 42, 43).

Y = a + b*X (41),

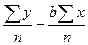b= (42), a = (43),

где n – объем выборки.

5. Оценка значимости, типичности.

6. Задание условий прогнозного периода (вероятных значений параметра X).

7. Прогнозирование возможных значений параметра Y при заданных значениях параметра X.