Расчет множественной регрессии
(3-4 стр теория)
Ввиду четкой интерпретации параметров наиболее широко используется линейная функция
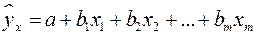 .
.
В линейной множественной регрессии параметры при 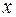 называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Рассмотрим линейную модель множественной регрессии с двумя переменными
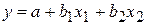 . (2.1)
. (2.1)
Система уравнений для нахождения коэффициентов множественной линейной регрессии имеет вид
Для двухфакторной модели данная система будет иметь вид:
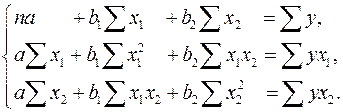
Для характеристики полученного уравнения можно использовать средние коэффициенты эластичности по каждому фактору
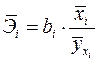 , (2.11)
, (2.11)
которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.
Рассмотрим пример(для сокращения объема вычислений ограничимся только десятью наблюдениями). Пусть имеются следующие данные (условные) о сменной добыче угля на одного рабочего 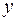 (т), мощности пласта
(т), мощности пласта 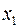 (м) и уровне механизации работ
(м) и уровне механизации работ 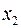 (%), характеризующие процесс добычи угля в 10 шахтах.
(%), характеризующие процесс добычи угля в 10 шахтах.
Таблица 2.2
| № | ||||||||||
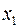
| ||||||||||
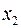
| ||||||||||
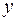
|
Предполагая, что между переменными 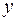 ,
, 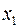 ,
, 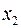 существует линейная корреляционная зависимость, найдем уравнение регрессии
существует линейная корреляционная зависимость, найдем уравнение регрессии 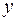 по
по 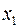 и
и 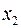 .
.
Для удобства дальнейших вычислений составляем таблицу ( 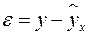 ) в excel:
) в excel:
Таблица 2.3
| № | 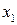
| 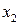
| 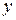
| 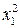
| 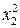
| 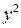
| 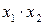
| 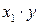
| 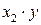
| 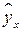
| 
|
| 5,13 | 0,016 | ||||||||||
| 8,79 | 1,464 | ||||||||||
| 9,64 | 0,127 | ||||||||||
| 5,98 | 1,038 | ||||||||||
| 5,86 | 0,741 | ||||||||||
| 6,23 | 0,052 | ||||||||||
| 6,35 | 0,121 | ||||||||||
| 5,61 | 0,377 | ||||||||||
| 5,13 | 0,762 | ||||||||||
| 9,28 | 1,631 | ||||||||||
| Сумма | 6,329 | ||||||||||
| Среднее значение | 9,4 | 6,3 | 6,8 | 90,8 | 41,7 | 49,6 | 60,3 | 66,4 | 44,5 | – | – |
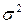
| 2,44 | 2,01 | 3,36 | – | – | – | – | – | – | – | – |
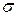
| 1,56 | 1,42 | 1,83 | – | – | – | – | – | – | – | – |
Для нахождения параметров уравнения регрессии в данном случае необходимо решить следующую систему нормальных уравнений:
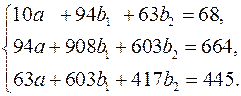
Решаем ее в excel применяя поиск решения. в результате находим
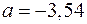 ,
, 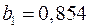 ,
, 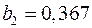 .
.
Т.е. получили следующее уравнение множественной регрессии:
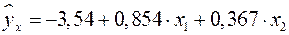 .
.
Оно показывает, что при увеличении только мощности пласта 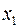 (при неизменном
(при неизменном 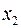 ) на 1 м добыча угля на одного рабочего
) на 1 м добыча угля на одного рабочего 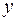 увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ
увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ 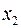 (при неизменном
(при неизменном 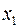 ) на 1% – в среднем на 0,367 т.
) на 1% – в среднем на 0,367 т.
Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности (2.11):
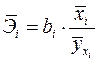 .
.
Вычисляем:
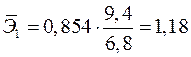 ,
, 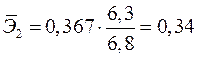 .
.
Т.е. увеличение только мощности пласта (от своего среднего значения) или только уровня механизации работ на 1% увеличивает в среднем сменную добычу угля на 1,18% или 0,34% соответственно. Таким образом, подтверждается большее влияние на результат 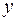 фактора
фактора 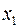 , чем фактора
, чем фактора 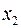
Дата добавления: 2016-04-22; просмотров: 814;
