Признаки сходимости Даламбера и Коши, радикальный признак Коши
Рассмотрим числовой ряд 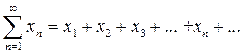 , (1) с неотрицательными или даже положительными членами
, (1) с неотрицательными или даже положительными членами 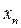 . В признаке Даламбера исследуется величина
. В признаке Даламбера исследуется величина 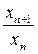 , в признаке Коши под нашим микроскопом окажется величина
, в признаке Коши под нашим микроскопом окажется величина 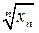 .
.
Теорема 1. (Признак Даламбера) Пусть для числового ряда (1) с положительными членами 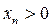 выполнено, начиная с некоторого номера (при
выполнено, начиная с некоторого номера (при 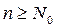 ), условие
), условие 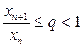 (2). Тогда ряд (1) сходится. Если же
(2). Тогда ряд (1) сходится. Если же 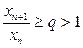 (3), то ряд (1) расходится.
(3), то ряд (1) расходится.
Доказательство. Не теряя общности, можно считать, что условия (2), (3) выполнены для всех 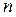 . Следовательно, в случае (2)
. Следовательно, в случае (2) 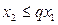 ,
, 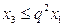 , …,
, …, 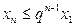 ,… и положительные члены ряда (1) не превосходят членов бесконечно убывающей геометрической прогрессии
,… и положительные члены ряда (1) не превосходят членов бесконечно убывающей геометрической прогрессии 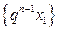 ,
,  . По признаку сравнения ряд (1) сходится. При выполнении условия (3) общий член ряда (1) не стремится к 0 и ряд (1) расходится по необходимому признаку сходимости. Теорема доказана.
. По признаку сравнения ряд (1) сходится. При выполнении условия (3) общий член ряда (1) не стремится к 0 и ряд (1) расходится по необходимому признаку сходимости. Теорема доказана.
Теорема 2. (Предельный признак Даламбера) Пусть для числового ряда (1) с положительными членами 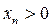 выполнено условие
выполнено условие 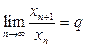 (4). Тогда при
(4). Тогда при  ряд (1) сходится, при
ряд (1) сходится, при 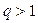 ряд (1) расходится. Если же
ряд (1) расходится. Если же  , то ряд (1) может и сходиться и расходиться, т. е. в этом случае требуется дополнительное исследование.
, то ряд (1) может и сходиться и расходиться, т. е. в этом случае требуется дополнительное исследование.
Доказательство. Пусть в условиях теоремы  . Из определения предела следует, что для положительного числа
. Из определения предела следует, что для положительного числа 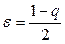 найдется номер
найдется номер 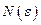 такой, что при
такой, что при 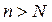 будет выполняться условие
будет выполняться условие 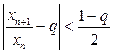 . Это равносильно двойному неравенству
. Это равносильно двойному неравенству 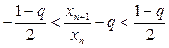 , которое преобразуется к виду
, которое преобразуется к виду  и по теореме 1 числовой ряд сходится. Пусть теперь
и по теореме 1 числовой ряд сходится. Пусть теперь  . Из определения предела следует, что для положительного числа
. Из определения предела следует, что для положительного числа  найдется номер
найдется номер 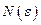 такой, что при
такой, что при 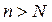 будет выполняться условие
будет выполняться условие  . Это равносильно двойному неравенству
. Это равносильно двойному неравенству 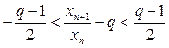 , которое преобразуется к виду
, которое преобразуется к виду  и по теореме 1 числовой ряд расходится. Теорема доказана.
и по теореме 1 числовой ряд расходится. Теорема доказана.
Теорема 3. (Признак Коши) Пусть для числового ряда (1) с неотрицательными членами  выполнено, начиная с некоторого номера (при
выполнено, начиная с некоторого номера (при 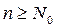 ), условие
), условие 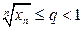 (5). Тогда ряд (1) сходится. Если же
(5). Тогда ряд (1) сходится. Если же 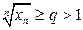 (6), то ряд (1) расходится.
(6), то ряд (1) расходится.
Доказательство. Не теряя общности, можно считать, что условия (5), (6) выполнены для всех 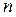 . Следовательно, в случае (5)
. Следовательно, в случае (5) 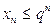 и положительные члены ряда (1) не превосходят членов бесконечно убывающей геометрической прогрессии
и положительные члены ряда (1) не превосходят членов бесконечно убывающей геометрической прогрессии 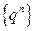 ,
,  . По признаку сравнения ряд 31) сходится. При выполнении условия (6) общий член ряда (1) не стремится к 0 и ряд (1) расходится по необходимому признаку сходимости. Теорема доказана.
. По признаку сравнения ряд 31) сходится. При выполнении условия (6) общий член ряда (1) не стремится к 0 и ряд (1) расходится по необходимому признаку сходимости. Теорема доказана.
Теорема 4. (Предельный признак Коши) Пусть для числового ряда (1) с неотрицательными членами  выполнено условие
выполнено условие 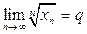 (7). Тогда при
(7). Тогда при  ряд (1) сходится, при
ряд (1) сходится, при 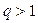 ряд (1) расходится. Если же
ряд (1) расходится. Если же  , то ряд (1) может и сходиться и расходиться, т. е. в этом случае требуется дополнительное исследование.
, то ряд (1) может и сходиться и расходиться, т. е. в этом случае требуется дополнительное исследование.
Доказательство. Пусть в условиях теоремы 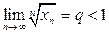 . Из определения предела следует, что для положительного числа
. Из определения предела следует, что для положительного числа 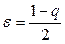 найдется номер
найдется номер 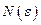 такой, что при
такой, что при 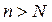 будет выполняться условие
будет выполняться условие 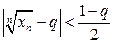 . Это равносильно двойному неравенству
. Это равносильно двойному неравенству 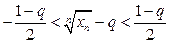 , которое преобразуется к виду
, которое преобразуется к виду 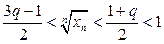 и по теореме 1 числовой ряд сходится. Пусть теперь
и по теореме 1 числовой ряд сходится. Пусть теперь 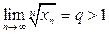 . Из определения предела следует, что для положительного числа
. Из определения предела следует, что для положительного числа  найдется номер
найдется номер 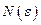 такой, что при
такой, что при 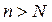 будет выполняться условие
будет выполняться условие  . Это равносильно двойному неравенству
. Это равносильно двойному неравенству 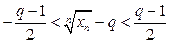 , которое преобразуется к виду
, которое преобразуется к виду  и по теореме 1 числовой ряд расходится. Теорема доказана.
и по теореме 1 числовой ряд расходится. Теорема доказана.
Замечание. Для полного доказательства теорем 2 и 4 надо привести 2 примера, когда  и один числовой ряд сходится и другой расходится. Это соответственно ряды с общими членами
и один числовой ряд сходится и другой расходится. Это соответственно ряды с общими членами  и
и 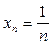 .
.
Приведем без доказательства еще одну теорему.
Теорема 4. (Предельный радикальный признак Коши) Пусть для числового ряда (1) с неотрицательными членами  выполнено условие
выполнено условие  (7). Тогда при
(7). Тогда при  ряд (1) сходится, при
ряд (1) сходится, при 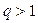 ряд (1) расходится. Если же
ряд (1) расходится. Если же  , то ряд (1) может и сходиться и расходиться, т. е. в этом случае требуется дополнительное исследование.
, то ряд (1) может и сходиться и расходиться, т. е. в этом случае требуется дополнительное исследование.
| <== предыдущая лекция | | | следующая лекция ==> |
| МОЛОЧНОКИСЛОЕ БРОЖЕНИЕ | | | Неполное аэробное окисление органических субстратов |
Дата добавления: 2016-04-22; просмотров: 980;
