Признаки сравнения сходимости числового ряда

Теорема 1. (1-й признак сравнения числовых рядов) Пусть заданы 2 числовых ряда 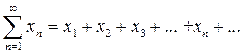, (1) и (2), при этом (3). Тогда из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).

Доказательство. Пусть сходится ряд (2). Это означает, что сходится последовательность соответствующих частичных сумм . По критерию Коши сходимости числовой последовательности последовательность сходится тогда и только тогда, грубо говоря, разность между членами последовательности, начиная с некоторого номера, становится сколь угодно малой. Конкретно это записывается следующим образом. Для каждого, сколь угодно малого положительного числа найдется натуральное число , обладающее тем свойством, что для любого натурального из выполнения условия следует выполнение неравенства . Это равносильно выполнению условия . В силу (3) справедлива и обратная цепочка неравенств, т. е. , далее , где . Следовательно, критерий Коши выполнен для ряда (6), что равносильно его сходимости. Докажем вторую часть теоремы методом от противного. Пусть теорема неверна и при расходимости ряда (1) сходится ряд (2). Но из только что доказанного в этом случае ряд (1) сходится. Полученное противоречие доказывает вторую часть теоремы. Теорема доказана.

Итак, смысл теоремы в том, что для рядов с неотрицательными членами из сходимости ряда с большими членами следует сходимость ряда с меньшими членами, а из расходимости ряда с меньшими членами следует расходимость рядов с большими членами.

Что произойдет, если изменить одно слагаемое числового ряда? Начиная с номера этого слагаемого все частичные суммы соответствующим образом изменятся на одну и ту же величину. Но это не меняет сам факт сходимости или расходимости числового ряда. Такое происходит и при изменении конечного числа слагаемых числового ряда.

Важное замечание. Изъятие, добавление, изменение конечного числа членов числового ряда не влияет на его сходимость.

Теорема 2. (2-й признак сравнения числовых рядов) Пусть заданы 2 числовых ряда 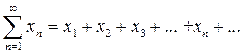, (1) и (2), при этом , (4). Тогда при условии (5) оба ряда (1) и (2) сходятся или расходятся одновременно.

Доказательство. Из условия (5) следует, что для каждого сколь угодно малого положительного числа , в частности для числа найдется натуральное число , обладающее тем свойством, что . Отсюда , что равносильно соотношениям . Теперь, начиная с номера выполнены соотношения: , , что, с учетом важного замечания и теоремы 1 доказывает теорему 2.