Определение числового ряда. Сумма ряда. Необходимое условие сходимости числового ряда. Свойства сходящихся рядов
Под словом «ряд» (по крайней мере, в этом разделе курса математики) мы будем понимать бесконечную сумму членов последовательности. Формально это звучит следующим образом. Для последовательности 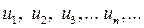 , построим сумму
, построим сумму 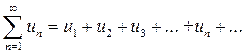 (1) этих объектов. Фактически мы должны определить, что понимается под такой бесконечной суммой. Члены ряда (1) могут являться числами или функциями.
(1) этих объектов. Фактически мы должны определить, что понимается под такой бесконечной суммой. Члены ряда (1) могут являться числами или функциями.
Пусть величины 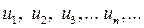 являются числами (пока действительными, но все сказанное можно отнести и к комплексным числам). Наряду с числовым рядом (1) рассмотрим последовательность его частичных сумм:
являются числами (пока действительными, но все сказанное можно отнести и к комплексным числам). Наряду с числовым рядом (1) рассмотрим последовательность его частичных сумм:  ,
, 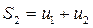 ,
,  ,…,
,…, 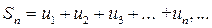 .
.
Определение 1. Числовой ряд (1) называется сходящимся, если существует предел его частичных сумм, причем в этом случае это число 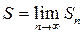 называется суммой числового ряда (1). В случае, если
называется суммой числового ряда (1). В случае, если 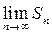 не существует, числовой ряд (1) называется расходящимся.
не существует, числовой ряд (1) называется расходящимся.
Если рассматривается числовой ряд, то мы чаще будем использовать обозначение 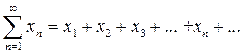 (
( 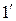 ).
).
Примеры. Рассмотрим числовые ряды:
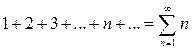 ,
, 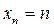 ; (2)
; (2)
 ,
, 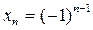 ; (3)
; (3)
 ,
, 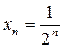 ; (4)
; (4)
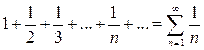 ,
, 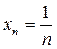 ; (5)
; (5)
Сходимость этих числовых рядов мы изучим, исходя из определения сходимости числового ряда и непосредственно исследуя их частичные суммы.
Для ряда (2) частичные суммы 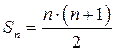 неограниченно возрастают. Их предел не существует (равен «плюс бесконечности»). Следовательно, числовой ряд (2) расходится.
неограниченно возрастают. Их предел не существует (равен «плюс бесконечности»). Следовательно, числовой ряд (2) расходится.
Для ряда (3) частичные суммы  ограниченны и поочередно принимают значения 1 и 0. Их предел не существует, следовательно, числовой ряд (3) расходится.
ограниченны и поочередно принимают значения 1 и 0. Их предел не существует, следовательно, числовой ряд (3) расходится.
Ряд (4) является известной нам суммой членов бесконечно убывающей геометрической прогрессии. Частичные суммы  имеют предел, равный 2. Следовательно, числовой ряд (4) сходится и его предел равен 2.
имеют предел, равный 2. Следовательно, числовой ряд (4) сходится и его предел равен 2.
Ряд (5) называется гармоническим рядом. Если его частичные суммы разбить на группы 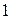 ,
,  ,
, 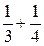 ,
,  ,
,  , …, то сумма слагаемых в каждой группе не меньше 0,5. Таких групп бесконечно много, следовательно, частичные суммы принимают сколь угодно большие значения и гармонический ряд (5) расходится.
, …, то сумма слагаемых в каждой группе не меньше 0,5. Таких групп бесконечно много, следовательно, частичные суммы принимают сколь угодно большие значения и гармонический ряд (5) расходится.
Надо понимать, что исследовать частичные суммы можно только в простейших случаях. В более сложных случаях мы будем применять теоремы, позволяющие ответить на вопрос о сходимости числового ряда. Простейшей из таких теорем является необходимый признак сходимости числового ряда.
Теорема 1. (Необходимый признак сходимости числового ряда) Если числовой ряд ( 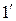 ) сходится, то выполнено условие
) сходится, то выполнено условие  .
.
Доказательство. Заметим, что 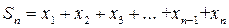 и
и 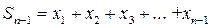 . Но при этом это две одинаковые последовательности и в случае их сходимости справедливо равенство
. Но при этом это две одинаковые последовательности и в случае их сходимости справедливо равенство 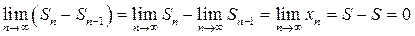 . Теорема доказана.
. Теорема доказана.
В чем смысл этой теоремы? Из сходимости числовой последовательности следует, что общий член этой последовательности стремится к 0. Но обратное, как показывает расходимость гармонического ряда, не всегда верно.
Какими свойствами обладают сходящиеся ряды?
Теорема 2. (Свойство сходящихся числовых рядов) Пусть числовые ряды 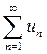 и
и 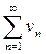 и при этом
и при этом 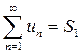 ,
,  . Тогда сходится ряд
. Тогда сходится ряд  и при этом
и при этом 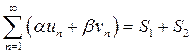
Доказательство. Это свойство вытекает из из определения суммы ряда, как предела соответствующих конечного числа слагаемых частичных сумм. Теорема доказана.
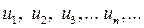 , построим сумму
, построим сумму 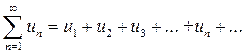 (1) этих объектов. Фактически мы должны определить, что понимается под такой бесконечной суммой. Члены ряда (1) могут являться числами или функциями.
(1) этих объектов. Фактически мы должны определить, что понимается под такой бесконечной суммой. Члены ряда (1) могут являться числами или функциями.
Пусть величины 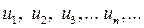 являются числами (пока действительными, но все сказанное можно отнести и к комплексным числам). Наряду с числовым рядом (1) рассмотрим последовательность его частичных сумм:
являются числами (пока действительными, но все сказанное можно отнести и к комплексным числам). Наряду с числовым рядом (1) рассмотрим последовательность его частичных сумм:  ,
, 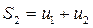 ,
,  ,…,
,…, 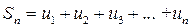 ,….
,….
Определение 1. Числовой ряд (1) называется сходящимся, если существует предел его частичных сумм, причем в этом случае это число 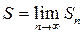 называется суммой числового ряда (1). В случае, если
называется суммой числового ряда (1). В случае, если 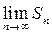 не существует, числовой ряд (1) называется расходящимся.
не существует, числовой ряд (1) называется расходящимся.
Если рассматривается числовой ряд, то мы чаще будем использовать обозначение 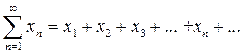 (
( 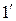 ).
).
Дата добавления: 2016-04-22; просмотров: 1185;
