Исчисление предикатов
Аппарат исчисления высказываний во многих случаях не позволяет удовлетворительно описать предметную область. Значительная часть предметных областей может быть описана средствами исчисления предикатов первого порядка. Для этого в рассмотрение вводятся:
а) константы, обозначающие индивидуальный объект или понятие;
б) переменные, которые в разное время могут обозначать разные объекты;
в) термы, простейшими из которых являются константы и переменные, а в более общем случае представляемые выражениями типа  , где
, где 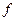 - функциональный символ, а
- функциональный символ, а 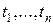 - термы;
- термы;
г) предикаты, используемые для представления отношений между объектами в некоторой предметной области;
д) кванторы – средство задания количественных характеристик предметной области.
Предикат – это логическая функция, принимающая только истинностные значения «истина» или «ложь».
Предикат состоит из предикатного символа и соответствующего ему упорядоченного множества термов, являющихся его аргументами. Предикатный символ P используется для именования отношений между объектами. Если он имеет n аргументов, то называется n-местным предикатным символом.
Запись 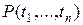 , являющаяся простейшей (атомарной) формулой, означает, что истинно высказывание: объекты
, являющаяся простейшей (атомарной) формулой, означает, что истинно высказывание: объекты  связаны отношением P.
связаны отношением P.
С помощью тех же логических связок, что и в исчислении высказываний (И, ИЛИ, НЕ, СЛЕДУЕТ, ЭКВИВАЛЕНТНО), можно строить более сложные формулы.
Для определения областей действия переменных в формулах используются кванторы 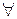 (всеобщности) и
(всеобщности) и 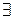 (существования). Кванторы позволяют строить высказывания о множестве объектов и формулировать утверждения, истинные для этого множества.
(существования). Кванторы позволяют строить высказывания о множестве объектов и формулировать утверждения, истинные для этого множества.
Формулы исчисления предикатов (ППФ – правильно построенные формулы) определяются рекурсивно следующим образом:
1. атом есть формула;
2. если A и B – формулы, то формулами являются и
ØA, A Ù B, A Ú B, A ® B, A « B;
3. если 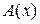 - есть формула, то формулами являются и
- есть формула, то формулами являются и 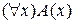 и
и 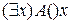 .
.
Интерпретация формул в исчислении предикатов – это задание областей значений всем константам, функциональным и предикатным символам. Формула, интерпретируемая на области D, принимает значения истина или ложь по следующим правилам:
а) если заданы значения формул A и B, то истинностные значения формул ØA, A Ù B, A Ú B, A ® B, A « B получаются по таблицам истинности, справедливым для исчисления высказываний;
б) формула 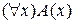 получает значение истина, если
получает значение истина, если 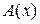 для каждого
для каждого  из D имеет значение истина, в противном случае ее значение – ложь.
из D имеет значение истина, в противном случае ее значение – ложь.
в) формула  получает значение истина, если
получает значение истина, если 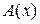 хотя бы для одного
хотя бы для одного  из D имеет значение истина, в противном случае ее значение – ложь.
из D имеет значение истина, в противном случае ее значение – ложь.
Формула A есть логическое следствие формул 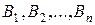 , тогда и только тогда, когда для любой интерпретации, в которой формула
, тогда и только тогда, когда для любой интерпретации, в которой формула 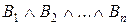 истинна, формула A также истинна.
истинна, формула A также истинна.
Кроме формул эквивалентных преобразований, приведенных для исчисления высказываний, в исчислении предикатов справедливы следующие:
Ø($  )
) 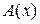 = (
= (  ) (Ø
) (Ø 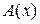 );
);
Ø( 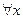 )
) 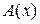 = (
= ( 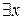 ) (Ø
) (Ø 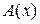 ).
).
Дата добавления: 2016-04-22; просмотров: 572;
