Математическая модель охлаждение провода. 2-ая модель охлаждения
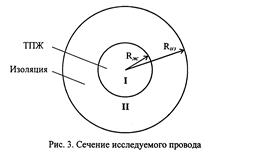Допущения:
1. процесс стационарный
2. теплофизические свойства постоянны и не зависят от температуры
3. диффузия тепла по оси Z мала
4. температура провода изменяется
Здесь индексы I и II обозначают материал ТПЖ и изоляции, соответственно.
Связь между изменением температуры в пространстве и во времени устанавливается на основе первого закона термодинамики и закона Био - Фурье и выражается дифференциальным уравнением теплопроводности. Это уравнение в цилиндрической системе координат имеет следующий вид:
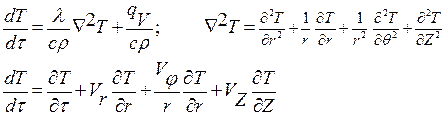
С учетом допущений:
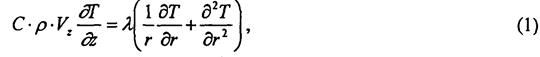
где С (Дж/(кгК)- удельная теплоемкость материала; р (кг/м3) - плотность;
VZ (м/с)- скорость движения провода; Т (К) - температура провода;
l (Вт/(м К)) -теплопроводность; r (м) и Z (м)- координаты по радиусу и длине провода.
Для расчета процесса теплопроводности запишем систему определяющих уравнений с краевыми условиями:
НУ: Тн = Твых
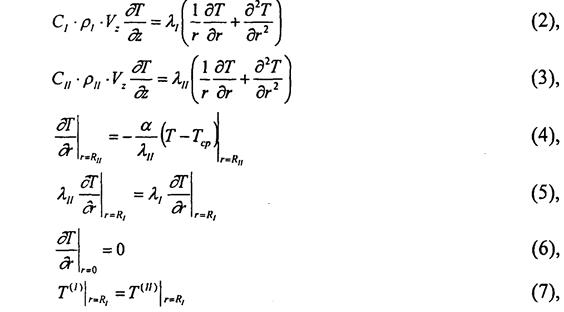
где l (Вт/м2 К)) - коэффициент теплоотдачи на поверхности изоляции.
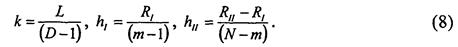
Таким образом, задавались следующие сетки в рассматриваемой области:
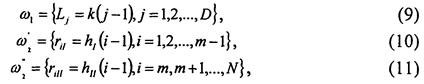
где Lj - текущее значение длины на участке охлаждения, ri I текущее значение радиуса по жиле, ri II - текущее значение радиуса по изоляции. Индексы j и i соответствуют номеру узла соответствующих сеток (9) - (11).
Разностная схема, позволяющая вычислять температуру на каждом следующем сечении по длине явно (т. е. не требуется решение систем линейных уравнений на каждом слое), называется явной схемой. Достоинством такой схемы является простота решения, а недостатком - условная сходимость.
Условия сходимости:
Заменяя исходную систему уравнений явной разностной схемой, получим следующую систему линейных алгебраических уравнений:
5 Расчёт напряжений по толщине ленточной изоляции из МЕХАНИЧЕСКОЙ ПРОЧНОСТИ лент
Свойства бумаги неоднородны, является ортотробной (свойство зависят от направления), так же бумага сжимаемый материал
Допущения
1. высокая плотность намотки
2. поддержание гибкостных характеристик
При изгибах силовых кабелей с бумажной пропитанной изоляцией, деформация последней происходит за счёт перемещения бумажных лент друг относительно друга. Условия перемещения лент определяются радиусом изгиба, коэффициентом трения и радиальным давлением на ленту. Это давление создаётся при изолировании за счёт определённого натяжения лент. Причём чем больше давление (выше плотность намотки), тем выше электрическая прочность изоляции.
Давление, создаваемое одной лентой определяется следующим образом:
 |
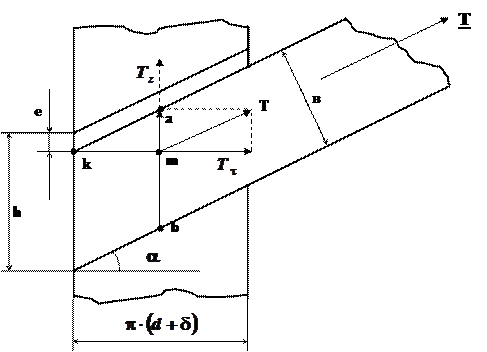Т – усилие натяжения ленты, накладываемой на ТПЖ
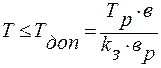, где
Тр – разрушающая нагрузка при растяжении
d – диаметр под обмотку
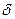- толщина ленты
в – ширина ленты
h – шаг обмотки
kз – коэффициент запаса прочности (3¸4)
вр – ширина ленты, при которой было пределено Тр; вр = 15 мм.
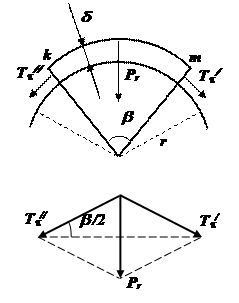
ab – линия касания ленты. К ней приложено усилие Tt
;
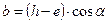a - угол обмотки
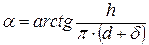, где h > b на 2¸3 мм, е = 0,5¸2 мм.
Tz – стремится сдвинуть витки вдоль оси кабеля (отвечает за устойчивость лент). Для ее уменьшения необходимо уменьшить угол a.
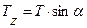
Tt -радиальное напряжение создает давление лент.
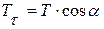; Tt приложим к ab; аb = b/cosa
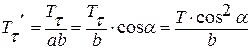- усилие на единицу длины.
По 3-му закону Ньютона:
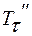обратная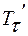 
= -
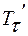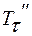
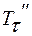- межмолекулярное взаимодействие.
; 
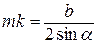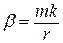[ рад ]
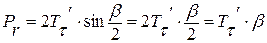
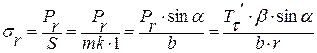
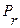- действует на площади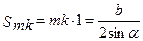 
Давление верхних лент на нижние:
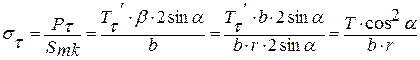
Давление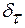 
тем больше, чем меньше угол a. Поэтому, чем выше напряжение кабеля, тем меньше допустимый угол изолирования.
a - должен быть нормирован иначе произойдет превышение соответствующих допустимых напряжений при изменении угла
Усилие 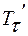подвергает бумажную ленту также и растяжению
; 
; 
.
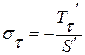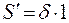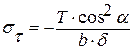Данные формулы справедливы для центральных ТПЖ, так как на внутренней поверхность лента ложится на несминаемый материал (σ = max), на внутренних лентах получается плато σ∞ - обусловлено сменаимостью Леты (происходит выравнивание напряжений по толщине изоляции).
На внешнюю ленту ничего не давит → σ = 0
 |
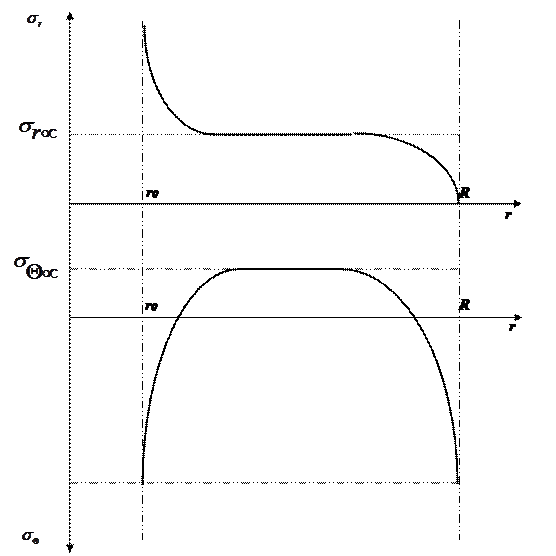r = R; σr = 0 , т.к. на внешнюю ленту ничего не давит
r = r0; σr = max, т.к. ленты накладываются на несжимаемый материал (жилу)
Результирующая рассчитывается:
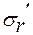- результирующее радиальное давление
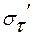- результирующее поперечное напряжение
Для 1 ленты изоляции:
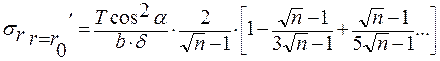
В остальной изоляции:
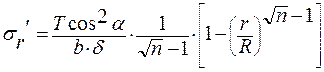
При уменьшении r выражение в скобках стремится к 1:
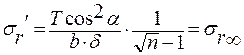
при r=R:
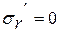
Поперечное давление рассчитывается:
· Для внутренних:
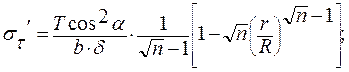
При достаточном расстоянии от R выражение в скобках стремится к 1:
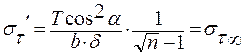
· Для первой и последней ленты:
r = r0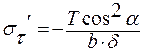 
r = R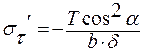
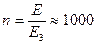
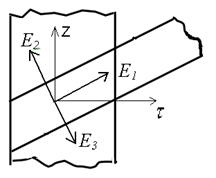Е – эквивалентный модуль упругости в направлении приложения силы Tt
E1 – модуль упругости вдоль ленты
Е1 = (5¸7)*109Па
Е2 – модуль упругости в поперечном направлении
Е2 = (2¸3)*109Па
Е3 – модуль упругости по толщине
Е3 = (5¸7)*106Па
G – модуль сдвига – характеризует усилие при котором будет происходить деформация в соответствующем направлении.
G = (1,4¸1,5)*109Па
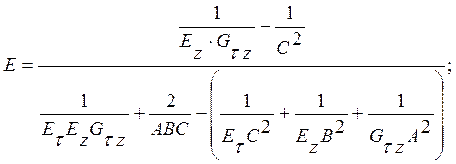
Gτz - характеризует усилие которое необходимо применить для сменания нашего изделия ( характеризует удлинение по ширине и длине)
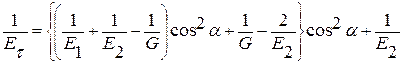
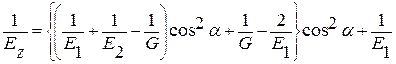
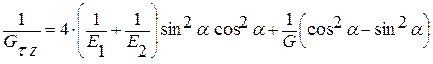
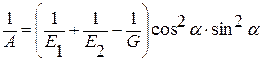
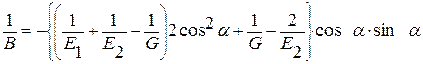
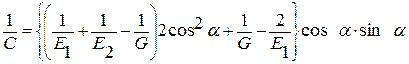
6 Расчет допустимого натяжения лент исходя из условия СМИНАНИЯ ленточной изоляции
При изгибе кабеля деформации изоляции происходят за счет перемещения лент относительно друг друга. При изгибе возникают 2 зоны: зона сжатия и зона растяжения. В зоне растяжения отрицательных явлений не возникает, так как прочность на разрыв у бумаги высока. В зоне сжатия ленты движутся друг к другу из – за осевых сил. Они направлены друг к другу и так как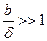 
то существует вероятность потери устойчивости бумаги над зазором , т. е. происходит образование складки, сминание бумажной ленты
· На внешней поверхности изгиба:
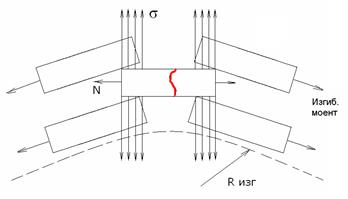N – сила действующая на разрыв.
Если Fтр велика, то может наступить разрыв.
По поверхности контакта образуются силы трения, которая зависит от коэффициента трения и напряжения σ. Если сила трения очень велика, то не будет свободного движения ленты относительно других лент и может произойти разрыв ленты.
· На внутренней поверхности:
а – перекрытие нижней ленты верхней (33%)[в долях единицы];
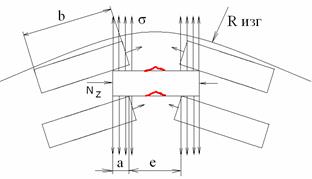в – ширина.
е - зазор
Nz – действует на сменание
ü На тпж накладывают ленты с перекрытием, так как основные напряжения воспринимает тпж.
ü На поверхности накладывают с перекрытием так как малые напряжения и обеспечивается свободный ход ленты.
Расчет из условия сменания:
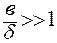
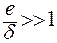(d - толщина ленты )
Основные силы зависят от радиального давления и коэффициента трения.
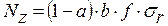,где
f – коэффициент трения; для непропитанной бумаги – 0,6;
σ – напряжение от натяжение ленты.
Условие устойчивости бумажных лент относительно появления складок и морщин
(Условие сменания):
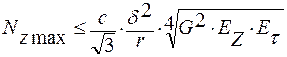, где
G – модуль сдвига
r – радиус слоя для которого идет расчет
с – коэффициент учитывающий неоднородности бумажной ленты (0,7 – 0,9)
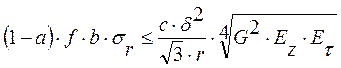
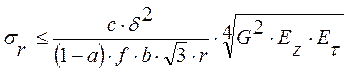- допустимое (1)
Рассчитать по (1) зависимость допустимого радиального давления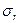 
от радиуса и сравнить со значением 
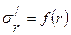(рассчитанное из ходя из механической прочности вопрос 5).Должно быть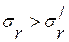 
Для 1 ленты изоляции:
В остальной изоляции:
(*)
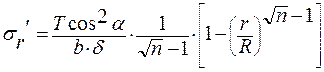Если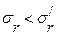 
, то следует уменьшить натяжение лент :
Из формулы (*) можно найти Тдоп, если вместо σ’r подставить σr рассчитанное по формуле (1).
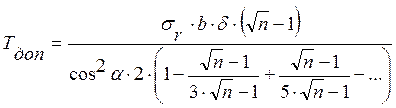; для первой ленты ( 
).
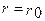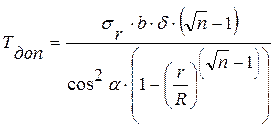; для всех остальных лент.
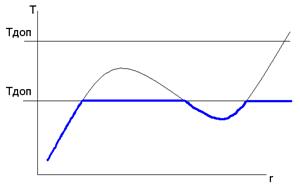
- из условия механической прочности
- из условия сменания
7 Расчёт напряжений по толщине сплошной полимерной изоляции в зависимости от приложенного внешнего давления. Постановка задачи. Численная реализация. Аналитическое решение.
В этой главе рассматриваются задачи линейной теории упругости,
выводы которой справедливы для :
1. тела однородного и изотропного, у которого между компонентами деформации и компонентами напряжений существует наиболее простая линейная связь (обобщенный закон Гука),
2. сами деформации предполагаются малыми, т. е. такими, когда компоненты деформации (относительные удлинения, относительные сдвиги) пренебрежимо малы по сравнению с единицей.
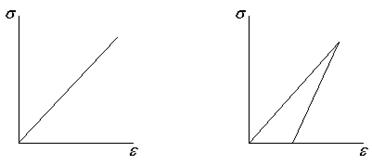
Лин. упруг. деформация Лин. НЕупргуг. деформация
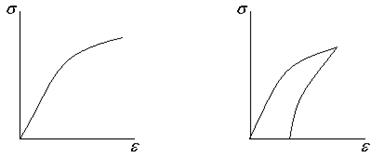
НЕлин. упруг. деформация НЕлин. Неупргуг. деформация
Для полимеров:
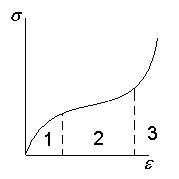1 – упругая деформация
2 – линейная неупругая денформация
3 – разрушение
У ПВХ 2 - НЕТ
Внутренние механическое напряжении – это внутренняя механическая реакция на действие внешней окружающей среды.
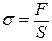F – сила, которая создает это напряжение, S – площадь к которому приложено напряжение.
Р – действует с наружи
σ – изнутри
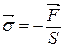
Абсолютное удлинение: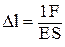 
1- единица длины, F – приложенная сила, Е – модуль упругости.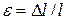 
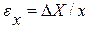
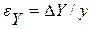
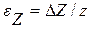
В цилиндрических координатах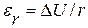 
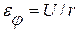
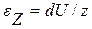
В простейшем случае для изотропного линейно-упругого тела эти уравнения (обобщенный закон Гука) записывают в форме:
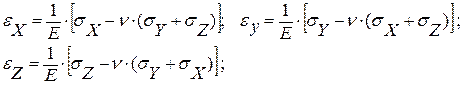
ν – кинематическая вязкость для твердого тела,
Коэффициент Пуассона (для полимеров = 0,1-0,5) показывает удлинение материала (без размерная величина) .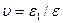 
- Объемное напряжение:
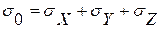
- Относительная объемная деформация:
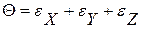
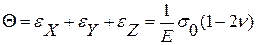
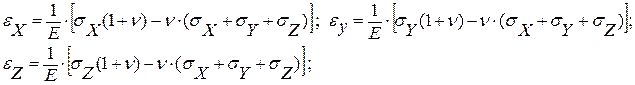
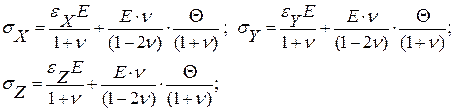
Коэффициенты Ляме :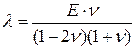 
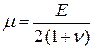
Выражение для внутренних напряжений
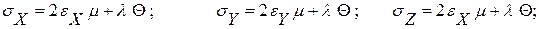
Допущения:
1. механическое напряжение вдоль оси Z малы (нагрузка идет на тпж) σZ =0
2. рассматриваем в цилиндрической системе координат
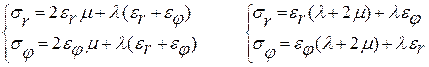
Уравнение Ляме для внут. механических напряжений
Уравнение равновесие:
Выражение 3 закон Ньютона 
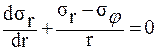
Механические напряжения компенсируются деформациями. Это выражение справедливо для упругой деформации
Математическая модель определения механического напряжения по толщине изоляции от внешнего давления
Математическая постановка задачи: используем толстостенный цилиндр h>>0.1*R
σr – направлено по R,
σφ – по касательной.
Допущения :
1. процесс стационарный
2. деформации вдоль оси Z пренебрежительно мала, напряжением вдоль оси Z пренебрегаем
3. среда однородна и изотропна
4. релаксационные процессы не учитываются
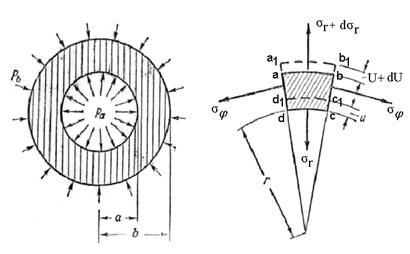
σ – внутренние механические напряжения
U – перемещение.
Уравнение равновесия:
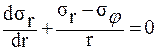
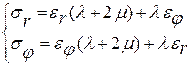
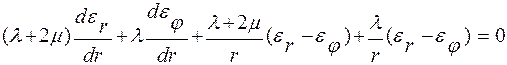
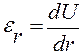
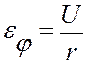
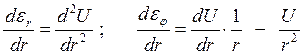
Уравнение равновесия в перемещениях:
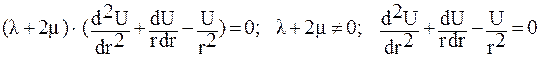
Для его решения нужно задаться ГУ
r = rВНУТ σr = - Рвнут
r = rНАР σr = - Рнар
Аналитический способ решение задачи Ляме
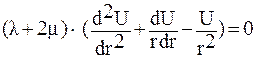
Решение этого уравнение имеет вид
U = A*r +B / r
A,B – коэффициенты зависящие от ГУ,
r – текущий радиус
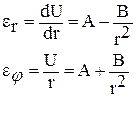
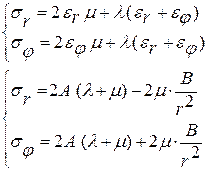
Для его решения нужно задаться ГУ и найти коэф. А и В:
r = rВНУТ σr = - Рвнут = 2А (λ+μ)-2μ В/ rВНУТ2
r = rНАР σr = - Рнар = 2А (λ+μ)-2μ В/ rНАР2
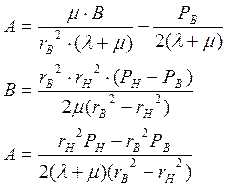
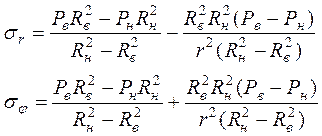
Численный метод решение задачи Ляме
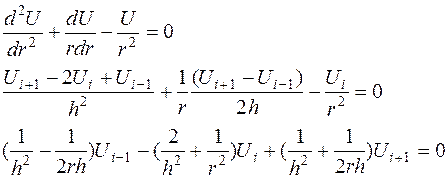
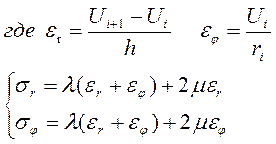
Граничные условия:
_________________________________________________________________________
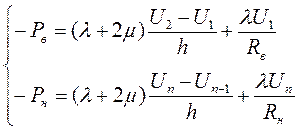
Дополнение:
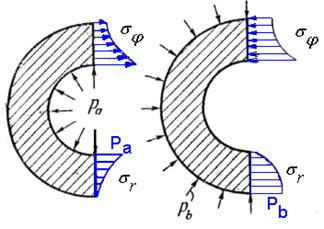Слева случай когда только внутренне давление
Справа – только внешнее
Дата добавления: 2016-04-19; просмотров: 1011;