Расчет сложных трубопроводов
Ранее изложенная методика гидравлического расчета предполагает, что диаметр нефтепровода по длине не меняется. Такой трубопровод принято называть простым.
В действительности при постоянной величине внешнего диаметра труб нефтепровода внутренний диаметр меняется с изменением толщины стенок труб. Кроме того, на отдельных участках прокладываются параллельные трубопроводы (лупинги и резервные нитки). Такой трубопровод принято называть сложным.
В общем случае сложный трубопровод можно рассчитывать по отдельным участкам. Далее общие потери напора определяются как сумма потерь напора последовательно соединенных участков. На участках с параллельными нитками потери напора принимаются равными потерям напора в одной из них.
Для облегчения расчета используется замена расчета сложного трубопровода расчетом простого трубопровода использованием понятий эквивалентного диаметра и коэффициента расхода.
Эквивалентным диаметром принято называть диаметр простого трубопровода, пропускная способность которого равна пропускной способности реального нефтепровода при прочих равных условиях.
Эквивалентный диаметр определяется последовательным упрощением сложного трубопровода, используя формулы определения эквивалентного диаметра при параллельном и последовательном соединении участков.
При параллельном соединении n участков
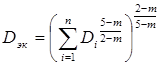, (4.35)
где Dэк – эквивалентный диаметр; Di – диаметр каждой из ветвей сложного участка.
При последовательном соединении n участков
, (4.36)
где Di – диаметр каждого из n последовательно соединенных участков; li – длина участка одного диаметра; L – суммарная длина последовательно соединенных участков.
Коэффициентом расхода Kр называют отношение пропускной способности нефтепровода данного диаметра Q к пропускной способности эталонного нефтепровода Q0, при прочих равных условиях.
. (4.37)
Эталонный диаметр D0 выбирается произвольно исходя из удобства расчетов. Обычно в расчётах принимают D0 = 1 м.
Коэффициент расхода простого трубопровода диаметром
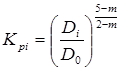. (4.38)
Для участка с параллельными нитками
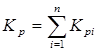(4.39)
Дата добавления: 2016-04-19; просмотров: 4780;