Точность и надежность статистической оценки

Понятие о распределении Стьюдента и хи–квадрат.Если случайная величина X подчинена нормальному закону, то для оценки параметров и проверки различных гипотез относительно этих параметров необходимо знание точного распределения некоторых выборочных характеристик. Например, для нахождения распределения эмпирической дисперсии необходимо исследовать распределение характеристик случайной величины, представляющей собой сумму квадратов n независимых случайных величин 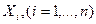, каждая из которых подчиняется нормальному закону с параметрами a=0 и .

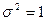Распределение случайной величины, удовлетворяющей этим условиям, называют хи–квадрат распределением или 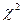- распределениемс k=n степенями свободы.

Число степеней свободы равно числу независимых переменных минус число связей, накладываемых на эти переменных. Если величины 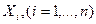связаны одним линейным соотношением, например, 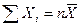, то число степеней свободы k=n-1.

Дифференциальная функция 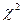- распределения для нее имеет вид

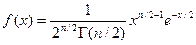при x>0, f(x)=0 при x<=0. Здесь

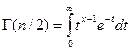- гамма – функция.

В частности, если x=n, то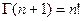

Для дифференциальной функции 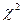- распределения из-за ее сложности составлены таблицы, позволяющие вычислять вероятности 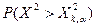, того, что случайная величина, распределенная по закону 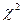с известным числом степеней свободы k, превысит некоторое фиксированное значение .

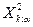График плотности вероятности 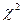- распределения при числе степеней свободы n=1, 2 и 6 изображен на рис. 5.3.

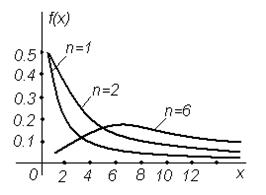
Рисунок 5.3 - График плотности вероятности 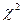- распределения

Распределение статистики 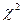не зависит ни от математического ожидания случайной величины X, ни от дисперсии, а зависит лишь от объема выборки n. Если случайная величина имеет 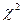распределение с k=n степенями свободы, то математическое ожидание и дисперсия соответственно равны: .

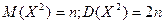Пример. Случайная величина имеет 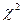- распределение с числом степеней свободы 5. Найти отклонение 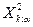, вероятность превышения которого равна 0.2.

Решение.

Из условия задачи следует, что надо найти такое значение 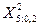, чтобы выполнялось равенство .

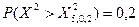Искомое значение 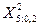ищется на пересечении строки 5 и столбца 0,2 таблицы (приложение). Оно равно 7,3, поэтому .

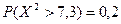Распределение 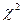обладает тем свойством, что сумма величин 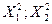, распределенные по закону 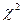со степенями свободы равными 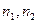, также распределена по закону 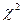с с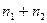тепенями свободы.

При решении многих задач статистики приходится иметь дело со случайными величинами, имеющими так называемое распределение Стьюдента или t-распределение. Это же распределение применяется при нахождении оценки отклонения выборочного среднего от центра нормального распределения.

Распределение Стьюдента имеет случайная величина

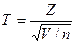, где Z – случайная величина, распределенная по нормальному закону с параметрами a=0 и 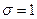; V – независимая от Z случайная величина, распределенная по закону 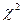с k=n степенями свободы.

Дифференциальная функция распределения Стьюдента имеет вид

.

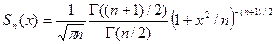Распределение Стьюдента обладает тем свойством, что с возрастанием числа степеней свободы оно быстро приближается к нормальному распределению (рис.5.4).

Рисунок. 5.4 – Графики нормального распределения и t - распределения

Доверительные границы для средних.Статистические оценки параметров распределения генеральной совокупности, рассмотренные ранее, являются точечными оценками. Если объем выборки невелик, то точечная оценка параметра может значительно отличаться от самого параметра. Поэтому в этих случаях применяют интервальную оценку. Задача интервальной оценки заключается в том, что по данным выборки строится такой числовой интервал (доверительный интервал), внутри которого с заранее заданной вероятностью, близкой к единице, будет находиться оцениваемый параметр.

Пусть для неизвестного параметра a найдена оценка 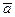и задана вероятность 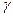, близкая к единице (доверительная вероятность). Требуется найти такое значение 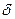, чтобы интервал 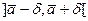длины 2 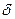накрыл искомое значение параметра a с вероятностью (надежностью) 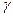, иначе говоря, выполнялось равенство

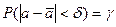или .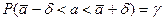

Безусловно, чем меньше длина интервала, тем точнее оценка искомого параметра a. При этом выбор доверительной вероятности (надежности) не является математической задачей, а определяется условиями задачи.

Например, пусть на двух предприятиях вероятность выпуска стандартных изделий равна 0,99, т.е. вероятность бракованных изделий равна q=0,01. Мала или велика эта вероятность? Для ответа на этот вопрос необходимо знать характер выпускаемой продукции. Пусть одно предприятие выпускает гвозди, а другое – парашюты. Если из 100 гвоздей один окажется бракованным, то с этим в какой-то степени можно мириться. Если же из каждых 100 парашютов один будет бракованным, то это может привести к многочисленным несчастным случаям, что недопустимо.

Задача построения доверительного интервала для оценки математического ожидания нормального распределения при известном среднем квадратичном отклонении 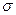сводится к следующему.

Обозначим неизвестное математическое ожидание через a, оценку же для него - .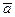

Для нормального распределения

; ; .

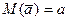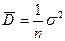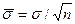Найдем доверительный интервал, покрывающий неизвестный параметр a с надежностью 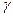, т.е. найдем такое 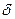, чтобы выполнялось равенство

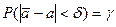. (5.6)

Для этого воспользуемся формулой

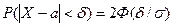, где Ф(x) – интеграл вероятности.

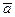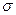Заменив в ней X на и на 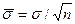, получим

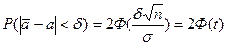, где .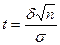

На основании равенства (5.6) можем записать, что

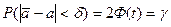, отсюда .

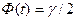Число t определяется по таблице значений функции Лапласа. Затем из соотношения 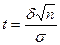находится оценка 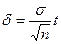. С учетом этого доверительный интервал будет

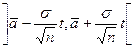. (5.7)

Пример. Случайная величина X имеет нормальное распределение с известным средним квадратичным отклонением 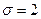. Построить доверительный интервал для неизвестного математического ожидания соответствующий доверительной вероятности 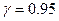, если объем выборки n=25.

Решение.

Найдем t из соотношения 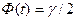. По таблице значений функции Лапласа находим t, соответствующее значению Ф(t)=0.95/2=0.475. Оно будет t=1.96.

Определяем точность оценки

.

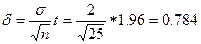Следовательно, доверительный интервал будет

.

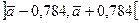Полученный результат говорит о том, что этот доверительный интервал покрывает неизвестное математическое ожидание a с вероятностью 0,95.

Задача построения доверительного интервала для оценки среднего квадратичного отклонения нормального распределения, покрывающего параметр 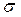с заданной надежностью 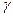по исправленному среднему квадратичному отклонению s.

Решение задачи сводится к нахождению такого числа 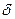, чтобы выполнялось равенство

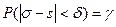или .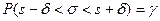

Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство 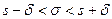в равносильное неравенство

.

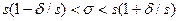Обозначив 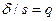, получим

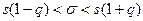. (5.8)

Таким образом, задача построения искомого доверительного интервала свелась к нахождению величины q.

Не вдаваясь в детали, отметим, что для этой цели вводится случайная величина X, равная

,

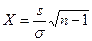дифференциальная функция которой имеет вид

.

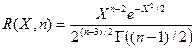Для нахождения доверительной вероятности используется формула

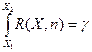, где .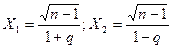

Из равенства (5.8) по заданному n и 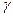находится значение .

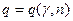Функция 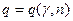табулирована.

Следовательно, для построения искомого доверительного интервала достаточно по таблице найти соответствующее значение функции 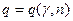, а затем в двойное неравенство 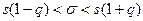подставить значения s и q.

Пример. Построить доверительный интервал, покрывающий генеральное среднее квадратичное отклонение 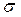с надежностью 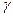, если по выборке объема n найдено исправленное среднее квадратичное отклонение s:

а)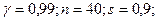

б) .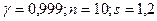

Решение.

По таблице значений функции 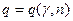находим:

а) 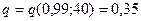; искомый доверительный интервал будет

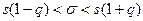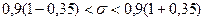; или

.

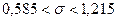б) 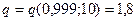; искомый интервал будет 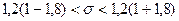или .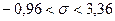

Так как среднее квадратичное отклонение 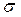всегда положительно, то окончательно получим, что .

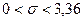Вопросы для повторения

1 Что понимают под законом больших чисел?

2 Сформулируйте теорему Чебышева и определите к чему сводится доказательство ее.

3 Сформулируйте теорему Бернулли и докажите ее.

4 Чем отличается выборка от генеральной совокупности и почему она должна быть представительной?

5 К определению каких статистик чаще всего сводится исследование выборки?

6 Как по статистическому распределению относительных частот выборки оценить вероятность попадания случайной величины в заданный интервал?

7 Объясните методику построения эмпирической функции распределения случайной величины по опытным данным.

8 Объясните методику построения гистограммы частот и относительных частот по опытным данным.

9 Чем отличаются процедуры оценки вероятности попадания случайной величины в заданный интервал по эмпирической функции распределения и по гистограмме относительных частот?

10 Какие требования предъявляют к оценкам числовых характеристик?

11 Что принимают в качестве оценок математического ожидания и дисперсии?

12 Чем отличается интервальная оценка от оценки точечной?

13 Как строится доверительный интервал для оценки математического ожидания нормального распределения при известном СКО?

14 Как строится доверительный интервал для оценки среднего квадратичного отклонения нормального распределения?

Упражнения

5.1 Из генеральной совокупности извлечена выборка объема n=50:

варианта 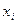2 5 7 10

частота 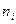16 12 8 14

Найти несмещенную оценку генеральной средней.

5.2 Из генеральной совокупности извлечена выборка объема n=60:

варианта 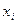1 3 6 26

частота 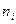8 40 10 2

Найти несмещенную оценку генеральной средней.

5.3 По выборке объема n=41 найдена смещенная оценка 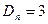генеральной дисперсии. Найдите несмещенную оценку дисперсии генеральной совокупности.

5.4 В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8; 9; 11; 12. Найдите выборочную среднюю результатов измерений.

5.5 В итоге пяти измерений некоторой длины стержня одним прибором получены следующие результаты: 92; 94; 103; 105; 106. Найдите выборочную среднюю длину стержня.