Прохождение частицы через потенциальный барьер . Туннельный эффект .

|
Это простейший прямоугольный барьер . Если задача классифицируется , то частица , обладая энергией Е просто пройдёт через барьер .
Для микрочастиц с Е >U имеется вероятность того , что частица отразится от барьера и будет двигаться с этой энергией .
При E<U частица окажется в области 0<x<l , то есть проникнет через потенциальный барьер .
Уравнение Шрёдингера даёт все эти решения , таким образом квантовая механика приводит к принципиально новому явлению , получившему название туннельного эффекта - явления в результате которого микрообъект может пройти через потенциальный барьер .
ГЛАВА 3. АТОМ.
3.1. Противоречия классической физики: стабильность и размеры атома, опыты Резерфорда, Франка и Герца
Они проводились с атомами ртути которые в виде паров находились внутри стеклянного баллона .Эти атомы взаимодействовали с электронами.
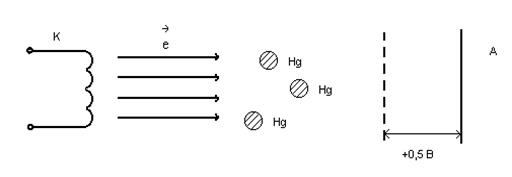
|
Схема установки :
Соударения носили или упругий , или неупругий характер.
1). Неупругое соударение - с потерей энергии.
2). Упругое соударение - без передачи энергии.
Когда измерили анодный ток , то зависимость носила следующий характер :
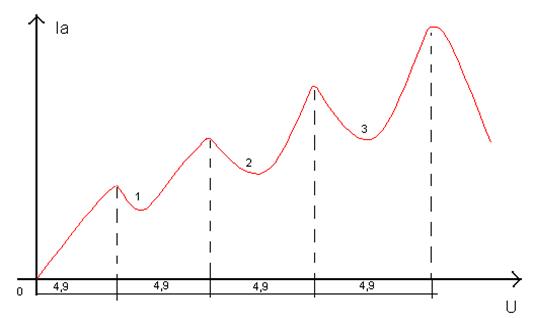
|
Участки 1,2,3 - неупругие соударения ,а максимумы - упругие соударения.
Атомы ртути поглощают энергию электронов не в любых количествах , а строго определённых - дискретно.
Wпогл = 4,9 эВ.
3.2. Частица в сферически симметричном поле. Атом водорода
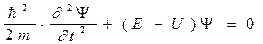
|
Потенциальная энергия для атома водорода имеет вид :
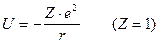
|
Z - порядковый номер в таблице Менделеева
r - радиус
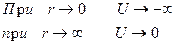
|
|
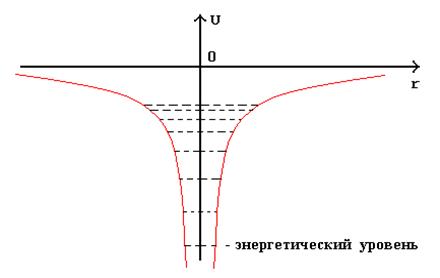
Энергетическая диаграмма потенциальной энергии электрона в атоме водорода имеет вид :
В данном случае говорится , что электрон находится в бездонной потенциальной . Если r = const , то U = const , то есть потенциальная яма имеет сферическую симметрию .
Запишем уравнение Шрёдингера в сферической системе координат :
r, Q , j - сферические координаты
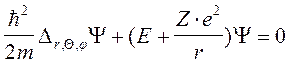
|
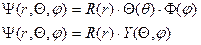
|
При подстановке этой функции в уравнение Шрёдингера , получим :

|
Они имеют решение , если 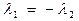 ,
,  .Первое уравнение имеет решение :
.Первое уравнение имеет решение :
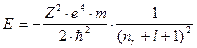
|
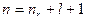 , то получим классическую энергию по Бору .
, то получим классическую энергию по Бору .
n - главное квантовое число
l - орбиталь .
При таком значении энергии первое уравнение допускает  решений ( n , l - целые числа ) .
решений ( n , l - целые числа ) .
Решение второго уравнения содержит сферические полиномы Лежандра . Они зависят от  , тогда решение уравнения Шрёдингера будет содержать произведение этих функций .
, тогда решение уравнения Шрёдингера будет содержать произведение этих функций .
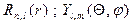 - частное решение уравнения Шрёдингера
- частное решение уравнения Шрёдингера
 - общее решение уравнения Шрёдингера .
- общее решение уравнения Шрёдингера .
Из решения уравнения Шрёдингера следует наличие квантовых чисел n , l , m
n- главное квантовое число (1,2,3 ...) , определяет энергию электрона в стационарном состоянии ;
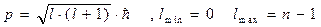
|
l - орбитальное квантовое число . Оно определяет момент количества движения (импульса) электрона на стационарной орбите .
m - максимальное квантовое число , определяющее проекцию момента импульса электрона на направление внешнего магнитного поля .
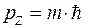 - проекция момента импульса .
- проекция момента импульса .
m = -l , -(l-1) ,... ,-2 ,-1 ,0 ,1 ,2 , ... ,(l-1) , l = 2l + 1 - общее число
Подсчитаем общее количество стационарных состояний в зависимости от m, l, n
N - общее число стационарных состояний :

|
Если n = 1 N = 1 , n = 2 N=4 , n = 3 N=9
| n | |||||||||
| l | |||||||||
| m | -1 | -2 | -1 |
3.3. Основное состояние атома водорода. Оценка энергии основного состояния .Устойчивость атома

|
Энергия атома водорода квантована , Z = 1
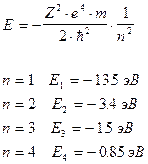
|
С помощью установки установим Iн пропорционально Ф и зависит от частоты 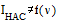 .
.
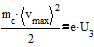 (*)
(*)
Факт (*) и то что vmax пропорционально частоте не мог быть объяснён классической физикой .
Размеры и стабильность атома .
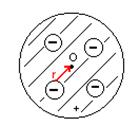
|
1910 г - первая модель атома Томсона p- плотность
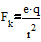
Fk - сила Кулона ;
 -формула квазиупругой силы
-формула квазиупругой силы
k-коэффициент , который включает параметры данной электрической системы .
Электрон в атоме должен колебаться и излучать.
Эта модель объясняет одну линию излучения , хотя наблюдается спектр.
1909-1913 модель Резерфорда .
Предполагаемый электрон вращается на орбите в виде шарика (классическая частица).
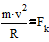

|
R- радиус ацс= при таком ускорении должен был излучать непрерывно
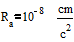
|
энергию и в результате упасть на ядро . Атом - стабильное образование и
3.4 Спин электрона, опыты Штерна и Герлаха. Пространственное распределение электрона в атоме водорода.
Проводились с атомами элементов I группы таблицы Менделеева , имеющих 1 валентный электрон . Наблюдали отклонение атомов в неоднородном магнитном поле
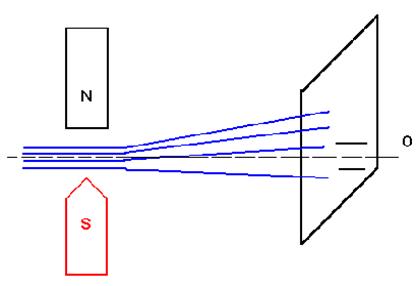
|
Электроны сталкивались и получался след на экране .
Дата добавления: 2016-04-19; просмотров: 1958;
