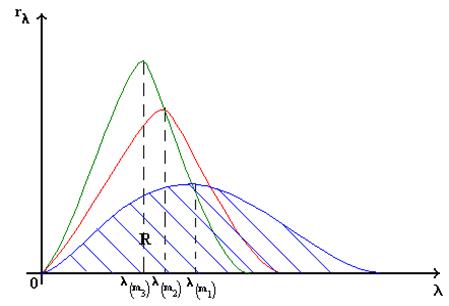
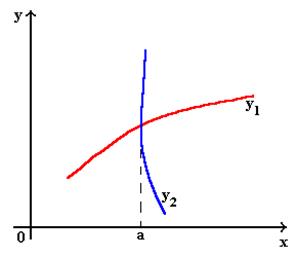
Закон смещения теплового изменения Михельсона - Вина .
|

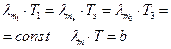 b- постоянная Михельсона - Вина
b- постоянная Михельсона - Вина

|
Особые точки , в которых функция имеет минимум :
1) n= 0
2) n= ¥
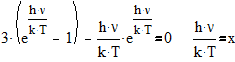
|
3)
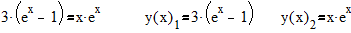
|
|
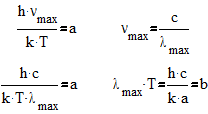
|
-закон смещения Михельсона-Вина.
ГЛАВА 2. КОРПУСКУЛЯРНО - ВОЛНОВОЙ ДУАЛИЗМ. КВАНТОВОЕ СОСТОЯНИЕ. УРАВНЕНИЕ ШРЕДИНГЕРА.
2.1.Гипотеза де Бройля и ее экспериментальное подтверждение. Дифракция электронов. Микрочастица в двухщелевом интерферометре.
Гипотезы Луи де Бройля.
|
1) Каждому свободному движению микрочастицы следует плоская монохромотическая волна .
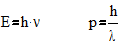
|
2) Энергия движения частицы связана с частотой формулой Планка :
-импульс
Е,р- характеристики частицы;
n,l- характеристики волны.
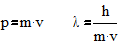
|
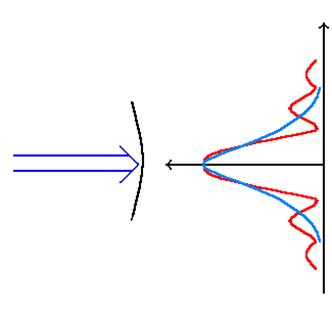
Девиссон и Джермер брали фольгу и ропускали через неё электороны при этом возникала дифракционная картина(см рис. выше).
2.2. Соотношения неопределённостей Гейзенберга и волновые свойства микрочастиц. Наборы одновременно измеримых величин.
Уравнение Шредингера .
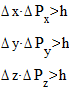
|
-соотношения неопределённостей Гейзенберга для координат и импульса.
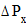
|
-погрешность измерения проекции импульса на ось х.
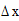
|
-погрешность измерения координаты х.
Соотношение неопределённости показывает , что невозможно точно измерить координату микрочастицы и соответствующую ей проекцию импульса.
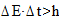
|
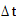
|
-погрешность измерения времени;
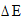
|
-погрешность в измерении энергии.
2.3. Задание состояния микрочастиц. Волновая функция; её статистический и физический смысл. Амплитуда вероятностей.
Проблемы о представлении волновой функции де Бройля и выяснения её физической природы привели к необходимости сравнения дифракции световых волн и микрочастиц.
Дифракционная картина , наблюдаемая для световых волн ,характеризуется тем , что при наложении дифракционных волн друг на друга в различных точках пространства происходит усиление или ослабление амплитуды колебаний.
Согласно волновым представлениям о природе света интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. По представлениям фотонной теории света : интенсивность определяется числом фотонов , попадающих в данную точку дифракционной картины. Следовательно число фотонов в данной точке дифракционной картины задаётся квадратом световой амплитуды световой волны . Значит для одного фотона квадрат амплитуды определяет вероятность попадания его в эту точку. Наличие максимумов дифракционной картины с точки зрения волновой теории означает : что эти точки соответствуют наибольшим интенсивностям волн де Бройля. С другой стороны интенсивность волн де Бройля оказывается больше там , где имеется большее число частиц . Таким образом дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности , согласно которой : частицы попадают в те места , где интенсивность волн де Бройля наибольшая .
В 1926 году Бор предположил что по волновому закону меняется не сама вероятность , а величина , называемая амплитудой вероятности :
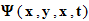
|
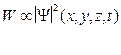
|
тогда амплитуда вероятности этой функции может быть комплексная и вероятность её W будет пропорциональна квадрату её модуля :

То есть описание состояния микрообъектов с помощью волновой функции Y имеет статистический (вероятностный) характер . И потому в квантовой механике состояние микрочастиц описывается с помощью волновой функции которая является основным носителем информации об их корпускулярных и волновых свойствах .Таким образом подобно уравнениям Ньютона , описывающим движение макротел , уравнение, названное уравнением Шрёдингера описывает движение микрочастиц.
Состояние движущейся микрочастицы и связанной с ней плоской монохроматической волны описывается данной Y-функцией , определяющей все параметры состояния в движении .
Выясним физический смысл Y-функции.
В соответствии с принципом неопределённости Гейзенберга мы не можем абсолютно точно указать местонахождение микрочастицы , а можем говорить об интервале в котором она находится .То есть вопрос о местонахождении микрочастицы мы толкуем в вероятностном смысле .
Волна характеризуется амплитудой интенсивности , то следовательно интенсивность функции будет пропорциональна следующим величинам :
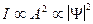
|
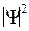
|
-плотность вероятности существования частицы в данной точке
dW - вероятность нахождения частицы в объёме dV :
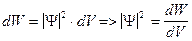
|
Физический смысл имеет квадрат модуля Y-функции.
2.4. Суперпозиция состояний в квантовой теории. Объяснение поведения микрочастицы в интерферометре
Волновая функция удовлетворяет принципу суперпозиций если система может находиться в различных состояниях , описываемых такими же функциями Y1 , Y2, ... Yn , где линейная комбинация их определяется :
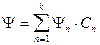
|
n=1,2,3,...,k
Сложение волновых функций то есть амплитуд вероятностей . В этом качестве отличие квантовой теории от классической статистической теории (механике Ньютона ) . В классической теории основной является теорема сложения вероятностей .
2.5 Временное уравнение Шредингера. Стационарное уравнение Шредингера. Стационарные состояния
Уравнение Шрёдингера сформулировано в 1926 году , оно не выводится , а постулируется . Правильность этого уравнения подтверждается согласием с опытом , с его результатами .
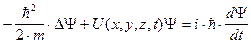
|
(1)
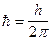
|
, D-оператор Лапласа , U(x , y , z , t) - потенциальная часть функции , определяющая энергию частицы в силовом поле в котором она движется .
Уравнение (1) действительно для частиц с малыми скоростями по сравнению со скоростью света .
В данном уравнении Y-функция должна удовлетворять следующим условиям :
1) Она должна быть конечной , однородной и непрерывной .
2) Её частные производные должны быть также непрерывными.
3) должна быть интегрируемой по всем направлениям
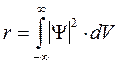
|
(2)
(2)-условие нормировки вероятности, общее уравнение Шрёдингера , зависящее от времени .
Для многих явлений , происходящих с микрочастицами уравнение можно упростить , для этого исключается зависимость Y от времени , то есть получаем уравнение Шрёдингера для стационарных состояний . Это возможно тогда , когда частица движется в стационарном поле . Для стационарной частицы уравнение Шрёдингера имеет вид :
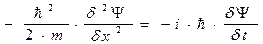
|
после упрощения получим :
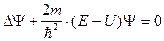
|
-уравнение Шрёдингера для стационарного состояния
E - полная энергия частицы .
В теории дифференциальных уравнений доказывается что подобные уравнения имеют бесчисленное множество решений . Из которых посредством наложения различных условий решения , имеющих физический смысл .
Регулярные решения данного уравнения имеют решение не для всех значений E , а лишь при определённом наборе этих значений .Эти значения носят название собственного значения функции .
Собственные значения E могут образовать как непрерывный , так и дискретный ряды . В первом случае говорится о непрерывном спектре . Во втором - о линейчатом спектре.
2.6. Частицы в одномерной прямоугольной яме. Прохождение частицы над и под барьером. Объяснение туннельного эффекта
|
Будем считать , что частица движется по х :
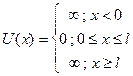
|
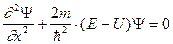
|
Если подставить эти пределы , то решение возможно в том случае если Y(0)=0 и Y(l)=0 , то есть граничные условия имеют вид (в пределах ямы ) :
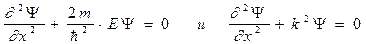
|
где 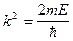
для данного уравнения Y-функция имеет вид :
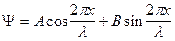
|
А и В = const , х- координата частицы , l- длина волны
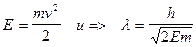
|
Рассмотрим два предельных случая , когда частица имеет координаты 0 и L , когда Y(l)=A sin kl =0 , если kL = np , где n- натуральные числа , тогда
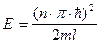 , то есть выражение для полной энергии зависит от числа n , так как ширина потенциальной ямы l и энергия частицы , находящейся внутри потенциальной ямы носят дискретный характер . То есть энергия частицы - квантованная величина .
, то есть выражение для полной энергии зависит от числа n , так как ширина потенциальной ямы l и энергия частицы , находящейся внутри потенциальной ямы носят дискретный характер . То есть энергия частицы - квантованная величина .
Дата добавления: 2016-04-19; просмотров: 1036;
