Единицы и стандарты пространства и времени

Системы координат. Системы отсчета.

1. Как уже было сказано во введении, в механике движением называют изменение положения тела в пространстве с течением времени. Под положением здесь понимается относительное положение, т. е. положение тела относительно других тел. Понятие абсолютного положения, т. е. положения тела в каком-то «абсолютном пространстве» безотносительно к другим телам, лишено содержания.

Тело или система тел, относительно которых определяется положение остальных тел, называется пространственной системой отсчета.

Утверждение, что два различных не одновременных события произошли в. одном и том же месте пространства, лишено содержания, пока не указана система отсчета, в которой события рассматриваются. Пассажир, в движущемся железнодорожном вагоне взял из своего чемодана какую-то вещь и спустя некоторое время положил ее обратно. Можно сказать, что он взял и положил эту вещь в одном и том же месте, если за систему отсчета принять движущийся вагон. Но те же два события будут происходить в различных местах, если их рассматривать в системе отсчета, связанной с полотном железной дороги. Например, одно событие внутри вагона могло произойти в Москве, а другое — в Ленинграде.

2. В качестве пространственной системы отсчета можно взять произвольное твердое тело и связать с ним координатные оси, например, декартовой прямоугольной системы координат, реализованные в виде трех взаимно перпендикулярных твердых стержней. Положение каждой точки в избранной пространственной системе отсчета можно задавать тремя числами: координатами точки х, у, z, представляющими собой .расстояния от этой точки до координатных плоскостей YZ, ZX, XY соответственно (рис. 1). Три координаты х, у, z можно объединить в один направленный отрезок или радиус-вектор r, проведенный из начала координат в рассматриваемую точку. Координаты х, у, z являются его проекциями на координатные оси, а потому

r = xi + yj + zk, (1)

где i, j, k – координатные орты, т.е. единичные векторы, направленные вдоль осей X, Y, Z.

Существуют два вида координатных систем: правая и левая. Их различают с помощью правила буравчика. Будем ввинчивать буравчик с правой нарезкой, вращая его ручку в плоскости XY кратчайшим путем от положительного конца оси X к положительному концу оси Y. В правой системе координат поступательное перемещение буравчика будет происходить в положительном, в левой - в отрицательном направлении оси Z. На рис. 1 представлена правая система, а на рис. 2 — левая.

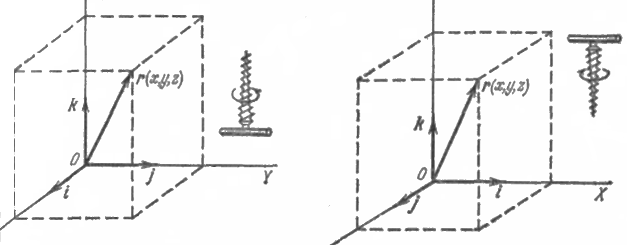
Рис. 1. Рис. 2.

Правая система никакими вращениями не может быть совмещена с левой. Обе системы отличаются друг от друга примерно так же, как правая рука отличается от левой. Но правая система переходит в левую, если изменить на противоположное положительное направление одной из координатных осей. То же самое произойдет, если изменить на противоположные положительные направления всех трех осей. Последняя операция называется инверсией координатных осей или отражением в начале координат. Например, изображением правой системы в плоском зеркале будет левая система, и наоборот. В физике применяется исключительно правая система.

3. Координаты х, у, z, которыми определяется положение точки в избранной системе отсчета, являются какими-то числами. Количественное определение этих координат, равно как и количественное определение всякой физической величины, сводится в конце концов к указанию принципиального способа их измерения. При этом имеются в виду именно принципиальные, а не практические способы измерения. Эти измерения должны лишь разъяснить смысл, точнее, принципиальный способ получения х, у, z, равно как и всяких чисел, с помощью которых количественно характеризуются все физические величины. Поэтому мы можем предполагать, что такие способы измерения являются идеальными, а самые измерения выполняются абсолютно точно. Координаты х, у, z являются длинами, а потому их нахождение сводится к измерению длин, т. е. к определению тех чисел, с помощью которых характеризуются длины. Когда мы говорим об измерении длин, то имеем в виду следующую измерительную операцию. Некоторый твердый стержень условно принимается за эталон, а его длина — за единицу длины. При измерении длины тела в каком-либо направлении определяется число, показывающее, сколько раз в этом направлении в теле укладывается выбранный эталон. Это число и называется длиной тела в рассматриваемом направлений. Если оно не целое, то предварительно длину эталона следует разделить на более мелкие части: десятые, сотые и пр. Используя их наряду с самим эталоном, можно представить длину всякого тела в виде десятичной дроби или целого числа с десятичной дробью.

4. Измерение длины непосредственным прикладыванием эталона или его частей называется прямым измерением. Прямые измерения не всегда возможны. Так, они невозможны при измерении расстояний до удаленных тел, например планет, звезд и других небесных объектов. Они невозможны и при измерении очень малых длин, например таких, с которыми имеет дело физика атома, атомного ядра или элементарных частиц, Во всех этих случаях применяют косвенные методы. Правильность таких методов должна контролироваться прямыми методами (разумеется, в тех случаях, когда последние применимы). За пределами же применимости прямых методов остаются одни только косвенные методы. Здесь прямые измерительные операции, с помощью которых первоначально было введено количественное понятие длины, становятся чисто умозрительными, а косвенные методы фактически играют роль основных принципиальных измерительных операций, которыми раскрывается смысл самих длин, или, точнее, тех чисел, которыми длины характеризуются.

Примером косвенного метода может служить триангуляция, применяемая для измерения расстояний до удаленных предметов. Прямым методом измеряют длину «базы» АВ, с концов которой делают «засечки» удаленного объекта С, т. е. измеряют, углы между базой АВ и прямыми АС и ВС. По этим данным искомое расстояние до объекта С может быть найдено геометрическим построением или вычислено по формулам геометрии. Если база АВ настолько велика, что ее длина не может быть найдена прямым измерением, то можно выбрать более короткую базу и затем найти, длину базы АВ описанным косвенным методом. Принципиально это ничего не меняет. Более существенно уяснить теоретическую основу метода. В методе предполагается, что сторонами треугольника АВС являются прямые линии, подчиняющиеся аксиомам геометрии Евклида. Но какими материальными объектами реализуются эти стороны? Такими объектами являются световые лучи, приходящие от объекта С к точкам А и В. Следовательно, в основе рассматриваемого способа лежит гипотеза, что световые лучи прямолинейны, т. е. подчиняются тем же аксиомам геометрии Евклида, что и геометрические прямые линии. Но эта гипотеза не очевидна. Доказать или опровергнуть ее можно только опытным путем. При этом имеются в виду световые лучи в вакууме, а не лучи в атмосфере, где они действительно искривляются из-за изменения показателя преломления от точки к точке. Такое искривление лучей может быть учтено и действительно учитывается, когда точность измерений этого требует.

Как можно убедиться в применимости или неприменимости геометрии Евклида к реальному миру в указанном выше смысле? Прямой метод состоит в том, что надо подвергнуть экспериментальной проверке следствия, выводимые из аксиом геометрии Евклида. Одним из таких следствий является, например, теорема, утверждающая, что сумма внутренних углов треугольника равняется 180°. Великий математик Гаусс (1777—1855) измерял в 1821—23 гг. со всей возможной тщательностью внутренние углы треугольника, образованного тремя удаленными горными вершинами. Длины сторон треугольника были порядка 100 км; Он нашел, что в пределах ошибок измерений не наблюдалось нарушений указанной теоремы. Этот метод не годится в масштабах Солнечной системы и бо’льших, так как все измерения производятся Земли, и мы не можем непосредственно измерить все три внутренних угла треугольника, вершинами которого помимо Земли являются, например, какие-либо две планеты или звезды. Здесь мы судим о применимости геометрии Евклида на основании косвенных данных — по согласованности различных результатов, полученных с использованием такой геометрии. Так, можно предвычислить, движение планет Солнечной системы на много лет вперед и проверить, полученные предсказания. Если бы они не оправдались, то одной из причин могла бы быть неприменимость геометрии Евклида к областям пространства порядка размеров Солнечной системы. Наоборот, согласие с опытом (что на самом деле имеет место) указывает на то, что сомневаться в применимости геометрии Евклида в областях такого размера нет оснований. Не вдаваясь в этот вопрос, ограничимся замечанием, что, по-видимому, нет существенных нарушений геометрии Евклида в областях порядка размеров нишей Галактики (~10²⁰ м) и даже Метагалактики, т. е. части Вселенной, доступной исследованию с помощью современных наиболее мощных телескопов (~10²⁶ м). Точно так же нет оснований ожидать существенных нарушений геометрии Евклида и в субатомных областях размером, скажем, порядка 10^{-15 м.}

Световые лучи при определении положения удаленных теп выполняют и другую важную функцию. Они служат теми материальными объектами, с помощью которых конструируется сама система отсчета. Действительно, твердые стержни не могут быть неограниченно длинными, а потому они не пригодны в качестве координатных осей во всем пространстве. Эту роль берут на себя световые лучи, являющиеся продолжениями в нужных направлениях координатных осей, первоначально реализованный твердыми стержнями.

5. В связи с выше изложенным, целесообразно сделать одно замечание о связи физики с математикой. Математика играет исключительно важную, роль, в физике. Без нее современная физика немыслима. Однако необходимо правильно представлять себе истинную роль математики в физике, и к этому вопросу мы еще будем неоднократно возвращаться. Чистая математика имеет, дело с абстрактными объектами и понятиями, подчиняющимися определенной системе аксиом. Единственное требование, предъявляемое в чистой математике к ее понятиям и аксиомам, сводится к их логической непротиворечивости. Все свои результаты чистая математика получает из этих аксиом путем логических рассуждений, основанных на правилах формальной логики. Содержание этих результатов, очевидно, не может выйти за пределы логических связей между различными объектами и понятиями чистой математики. В этом смысле чистая математика является логически замкнутой дисциплиной. Такая замкнутость и логическая согласованность придают чистой математике эстетическую привлекательность и доставляют чувство глубокого удовлетворения всякому уму, воспитанному в духе математической строгости.

Надо, однако, заметить, что строго замкнутая сама в себе математика оторвана от реальной действительности и не может быть использована в других науках и практической деятельности человека. Чтобы математика стала мощным средством при описании и изучении явлений природы, каким она в действительности является, необходимо установить связи между абстрактными математическими объектами и понятиями - с одной стороны — и реальными объектами и явлениями природы — с другой. Математические понятия и объекты должны появляться не как чисто логические категории, а как абстракции каких-то реальных объектов или процессов природы. Так, точка является абстракцией физического тела достаточно малых размеров, прямая линия — абстракцией достаточно тонкого твердого стержня или светового пучка в однородной среде. Вопрос о справедливости математики сводится к справедливости ее аксиом. Справедливость же самих аксиом может быть установлена опытным и только опытным путем.

Правда, опыт с математическими объектами нельзя осуществить в чистом виде, поскольку эти объекты являются идеализациями и не встречаются в природе. Всякий опыт выполняется с реальными телами. Математическую строгость, которой, и не без оснований, так гордятся математики, надо понимать в смысле логической согласованности ее выводов, но не в смысле обоснования математических аксиом.

Одной математической строгости недостаточно для физики, как и для всякой другой опытной науки, имеющей дело с реальными объектами и явлениями природы. Всякое теоретическое Исследование, даже выполненное математически строго, никогда не может считаться и физически строгим. Во-первых, такие исследования всегда основываются на определенных законах, справедливость которых в конце концов доказывается опытным путем, а опыты и физические измерения неизбежно сопровождаются ошибками, т. е. выполняются с определенной точностью. Вне пределов этой точности физический закон может оказаться не верным. Во-вторых, всякий реальный физический объект характеризуется бесконечным разнообразием свойств. Учесть все эти свойства невозможно не только потому, что большинство из них нам просто неизвестно, по и потому, что это практически не осуществимо. При построении теории физика заменяет реальные объекты их идеализированными моделями, приблизительно правильно передающими не все свойства реальных объектов, а только те из них, которые существенны в рассматриваемом круге, вопросов. Какие свойства реальных объектов существенны, а какие не играют заметной рели — на этот вопрос в конце концов может ответить только опыт, которому принадлежит решающее слово в вопросе о правильности всякой физической теории и пределах ее применимости. Если физический закон применен вне области, где он справедлив, а идеализированная модель правильно передает не все свойства реальных объектов, существенные для рассматриваемого круга явлений, то возникающие вследствие этого пороки теории, понятно, не могут быть исправлены никакой строгостью математических рассуждений и расчетов.

Последнее замечание имеет и практическую ценность. Конечно, после того как идеализированная модель построена, не будет ошибкой производить все дальнейшие расчеты математически абсолютно точно, хоти бы при этом и использовались физические законы, верные только приближенно. Однако сплошь и рядом такие расчеты очень громоздки и даже практически не осуществимы из-за их сложности. Между тем точность уже обесценена ошибками физических законов и несовершенствами идеализированной модели, положенной в основу расчета. Можно и нужно перейти к приближенным расчетам. Такие расчеты столь же хороши, что и «точные», если их ошибки не превосходят ошибок, обусловленных неточностью применяемых физических законов и несовершенствами идеализированных моделей.

Многие понятия и открытия, которыми по справедливости так гордится математика, не имеют никакого смысла, когда речь заходит о применении этих понятий к реальным объектам. Сюда относится, например, понятие иррационального числа. Лишено содержания утверждение, что физическая величина имеет иррациональное значение. Такое утверждение не может быть проверено. Одних только рациональных чисел достаточно, чтобы представить результаты измерений, выполненных со сколь угодно высокой степенью точности. Кроме того, понятие физической величины может утратить смысл, если к ее измерению предъявить требование неоправданно высокой точности. Так, например, совсем не ясно, о чем идет речь, если поставить задачу об измерении длины твердого стержня с точностью до размеров электрона или даже атома. Принципиально неограниченная точность измерения длин имеет смысл для абстрактных прямолинейных отрезков геометрии, а не для реальных тел, имеющих атомистическую структуру.

Несколько слов о стандарте длины.

Разумно в качестве стандарта использовать какую-то естественную единицу длины, например радиус Земли или некоторую его долю. Именно таким образом возник метр. Первоначально он определялся как (π/2)·10^-7 доля радиуса Земли. Однако такое определение нельзя считать ни особенно точным, ни удобным. Поэтому и течение долгого времени по международному соглашению в качестве эталона метра принималась длина между двумя Метками, сделанными на особом брусе, который хранится в специальной лаборатории во Франции. Только много позднее поняли, что такое определение метра не столь уж точно, как это необходимо, и не так уж универсально и постоянно, как этого хотелось бы. Поэтому сейчас принят новый стандарт длины как некоторое заранее установленное число длин волн определенной спектральной линии.