Спектральные и временные характеристики
Отклонение физической величины р(t) в звуковой волне от состояния покоя может быть определено для каждого момента времени (детерминированный процесс) и носить случайный неопределенный характер (случайный процесс). Примером процесса первого рода является шум вращения воздушного винта, звук сирены; примером процесса второго рода - шум воздушной струи. Совокупность детерминированных процессов может носить характер случайного процесса (рисунок 2.3), например наложение детерминированных шумов выхлопа отдельных автомобилей дает уличный шум, имеющий случайный характер.
Периодические процессы, повторяющиеся через время Т, называемое периодом, являются детерминированными. Кратковременные процессы всегда являются непериодическими.
Случайный процесс можно представить состоящим из большого числа кратковременных непериодических процессов, отличающихся друг от друга. Случайный процесс, средние статистические характеристики которого со временем не меняются, называется стационарным, хотя он состоит из неповторяющихся элементов.
Раньше шумом называли всякий звук случайного характера. В соответствии с установившейся в настоящее время терминологией шумом будем называть всякий нежелательный звук в слышимом диапазоне частот. Поэтому при рассмотрении физических характеристик поля на практике чаще используется термин «звук », а при описании источников звука или физиологического воздействия звукового поля на человека преимущественно применяется термин «шум».
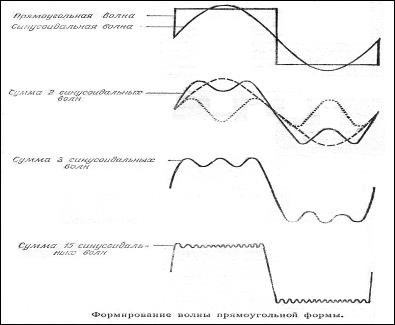
Рисунок 2.3
Спектр периодического процесса
В силу линейности уравнений акустики сложное колебание р(t) всегда можно представить в виде суммы (суперпозиции) более простых колебаний, например в виде суммы синусоидальных волн. Для периодического детерминированного процесса в какой-либо точке среды эта сумма будет иметь вид:
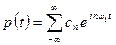 (2.24)
(2.24)
где n - целые числа, а основная круговая частота ω связана с периодом Т соотношением 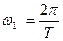 .
.
Величины С n являются комплексными амплитудами отдельных синусоидальных составляющих. Они выражаются формулой
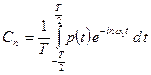 (2.25)
(2.25)
Процесс определения амплитуды Сп называется гармоническим анализом функции р(t), а величины Сп называются гармониками периодического процесса. Если учесть комплексность величины Сп, то выражение (2.24) можно представить в виде:
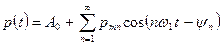
Величина А0 является постоянной слагающей; если рассматриваются отклонения физических величин в волне от невозмущенного состояния, то А0 = 0. Аргумент 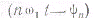 называется фазой колебания, ψn - начальной фазой. Максимальное отклонение ртп называется амплитудой. Индекс п называется номером гармоники; значению п=1соответствует первая гармоника или основная частота. Колебания с кратными друг другу частотами называются гармоническими составляющими.
называется фазой колебания, ψn - начальной фазой. Максимальное отклонение ртп называется амплитудой. Индекс п называется номером гармоники; значению п=1соответствует первая гармоника или основная частота. Колебания с кратными друг другу частотами называются гармоническими составляющими.
Зависимость амплитуд ртп или фаз ψn от частоты колебаний называется соответственно спектром амплитуд или фаз. Обычно в практике борьбы с шумом интерес представляет лишь абсолютная величина (модуль) гармоник ртп безотносительно к фазе ψn.
Средний квадрат периодической функции р(t), исходя из определения средней величины, равен:
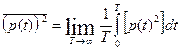 (2.26)
(2.26)
Проделав необходимые вычисления, получим для синусоидальных составляющих
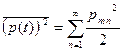 . (2.27)
. (2.27)
Это важная формула, так как она устанавливает связь мощности процесса (например, интенсивность звука в данной точке звукового поля) с амплитудами синусоидальных составляющих. Каждая величина 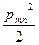 пропорциональна мощности синусоидальной составляющей с амплитудой Рmn. Таким образом, мощность периодического процесса равна сумме мощностей гармоник (энергетическое суммирование составляющих). Начальные фазы гармоник никакой роли при этом не играют.
пропорциональна мощности синусоидальной составляющей с амплитудой Рmn. Таким образом, мощность периодического процесса равна сумме мощностей гармоник (энергетическое суммирование составляющих). Начальные фазы гармоник никакой роли при этом не играют.
Зависимость 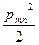 от частоты называется спектром мощности или энергетическим спектром данного процесса.
от частоты называется спектром мощности или энергетическим спектром данного процесса.
Среднее квадратическое значение физической величины 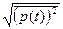 называется действующим или эффективным ее значением. Действующие значения гармоник выражаются через действующие значения амплитуд как
называется действующим или эффективным ее значением. Действующие значения гармоник выражаются через действующие значения амплитуд как 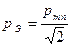 .
.
Процесс может состоять из некратных друг другу синусоидальных колебаний (почти периодический процесс, не являющийся периодическим), например сложение двух процессов с некратными друг другу периодами Т1 и Т2. В этом случае формула (2.27) также справедлива. Таким образом, средняя мощность любого детерминированного периодического или почти периодического процесса равна сумме мощностей его составляющих.
Спектр случайного процесса
Случайный процесс (каковыми в большинстве случаев являются шумы) не имеет резко выраженного периода и поэтому, в отличие от периодического процесса, не может быть выражен через гармонические составляющие. Однако он также обладает важными спектральными характеристиками.
Рассмотрим характеристику стационарного случайного шума. Установившимся во времени устойчивым процессам соответствуют обычно такие шумы, вероятностные характеристики которых не изменяются при любом сдвиге по времени. Если в бесконечной записи случайного процесса выделить несколько произвольных участков одинаковой продолжительности Т (такие участки называются реализациями данного случайного процесса) и наложить друг на друга, то записанные кривые не совпадут ни при каких Т.
Такой непрерывный процесс обладает средней мощностью и энергетическим спектром этой мощности, т. е. распределением ее по частотам колебаний. Средняя фаза в силу случайности колебания смысла не имеет.
Мощность такого процесса
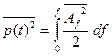 (2.28)
(2.28)
где 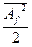 - средняя по времени мощность, приходящаяся на полосу частот шириной 1 гц.
- средняя по времени мощность, приходящаяся на полосу частот шириной 1 гц.
Зависимость 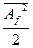 - от частоты называется энергетическим спектром данного случайного процесса или спектром его мощности. Величину
- от частоты называется энергетическим спектром данного случайного процесса или спектром его мощности. Величину 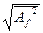 можно назвать эффективной амплитудой случайного процесса на частоте f, отнесенной к полосе шириной 1 гц.
можно назвать эффективной амплитудой случайного процесса на частоте f, отнесенной к полосе шириной 1 гц.
Вид спектра зависит от спектральных характеристик одиночных процессов, совокупность которых составляет случайный процесс, и от распределения их во времени.
Таким образом, средняя мощность периодического, почти периодического и случайного процессов равна сумме мощностей их синусоидальных составляющих.
Совсем другая .картина может наблюдаться, если складываются колебания от двух различных источников
P(t) = P1(t) + P2(t),
а не спектральные составляющие одного и того же .процесса. В этом случае:
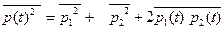 (2.29)
(2.29)
Процессы p1и р2называются некогерентными в том случае, если их взаимная мощность 2р1р2 равна нулю. Для независимых друг от друга процессов, как показывает теория вероятностей, это условие соблюдается всегда.
Степень причинной связи двух одновременных процессов характеризуется их моментом (функцией) корреляции
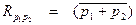 , (2.30)
, (2.30)
или нормированной величиной, называемой коэффициентом корреляции:
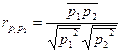 (2.31)
(2.31)
Условие равенства нулю коэффициента корреляции не всегда означает отсутствие причинной связи между составляющими, как .мы видели на примере синусоидальных составляющих одного и того же процесса.
При сложении двух процессов с одной и той же частотой они могут быть как когерентными, так и некогерентными (в зависимости от разности фаз составляющих).
Степень причинной связи во времени одного и того же случайного процесса характеризует функция автокорреляции
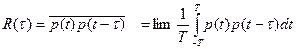 (2.32)
(2.32)
где τ — время задержки. Для стационарного случайного процесса R(τ) не зависит от момента времени, принятого за нуль.
Функция автокорреляции случайного процесса однозначно связана с его спектром мощности. Функция автокорреляции и спектр мощности полностью равноправны при описании случайного процесса.
Составляющие энергетического спектра стационарного случайного процесса сами являются случайными функциями времени, и их можно считать постоянными лишь при бесконечном времени усреднения. Реальные измерительные приборы обладают конечным временем усреднения, и поэтому показания их при измерениях спектра испытывают флуктуации случайного характера, размах которых зависит от свойств прибора и ширины полосы частот. Чем эта полоса 'больше, тем флуктуации меньше.
По этой же причине при сложении случайных звуков, а также периодических сигналов, отличающихся по частоте менее чем на 10 гц, слух человека различает биения, так как время осреднения человеческого уха составляет конечную величину порядка 1 00 мсек.
Графическоео изображение спектров.
Спектр периодического .процесса с основной частотой f1 изображается , в виде зависимости амплитуд составляющих от частоты (рисунок 2.4а). На графике откладываются отрезки, пропорциональные
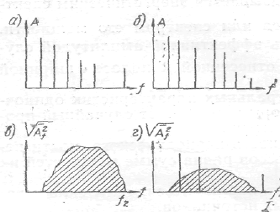
Рисунок 2.4
либо амплитудам, либо их квадратам. Начальные фазы нас не интересуют.
Спектр почти периодического процесса имеет такой же вид, только частоты не всех составляющих кратны друг другу {рисунок 2.4б). Спектры процессов, составленных из синусоид, называются дискретными или линейчатыми. Следует обратить внимание на то, что линии на таком спектре, теоретически рассуждая, не имеют ширины.
Спектр случайного или непериодического процесса (рисунок 2.4в) является оплошным, и поэтому его изображение требует обязательной оговорки о ширине ∆f элементарных полосок, к которым оно относится. По оси ординат откладываются, как показано на рисунке, либо средние квадратические значения эффективных амплитуд 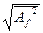 , либо соответствующие значения средних квадратов (энергий) в указанной полосе частот
, либо соответствующие значения средних квадратов (энергий) в указанной полосе частот
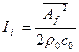 , либо действующее значение амплитуды
, либо действующее значение амплитуды 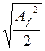 , либо уровни этих величин в дБ. Частота f1называется .нижней граничной частотой полосы спектра, а f2 — верхней. За среднюю частоту полосы обычно принимают среднюю геометрическую, равную
, либо уровни этих величин в дБ. Частота f1называется .нижней граничной частотой полосы спектра, а f2 — верхней. За среднюю частоту полосы обычно принимают среднюю геометрическую, равную
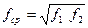 (2.33)
(2.33)
При оперировании с шумами их частотные .составляющие почти всегда считают некогерентными, и предполагают, что они подчиняются энергетическим соотношениям. Тогда, если известна эффективная амплитуда 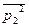 полосы ∆2 = f2-f1, то амплитуду
полосы ∆2 = f2-f1, то амплитуду 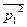 полоски ∆1f = 1 гц легко рассчитать по формуле
полоски ∆1f = 1 гц легко рассчитать по формуле
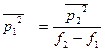 (2.34)
(2.34)
Обратный пересчет будет справедлив, если известно, что в диапазоне f2-f1 амплитуда 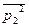 существенно не изменяется.
существенно не изменяется.
Спектр нескольких периодических и случайных процессов имеет смешанный характер (рисунок 2.4г) и изображается в виде наложения сплошного и дискретного спектров, причем совмещение их на одном графике является условным, так как амплитуда дискретной составляющей не зависит от ширины полосы спектра, а ордината сплошной части от этой ширины сильно зависит в соответствии с (2.34). Недопустимо распределять мощность дискретной составляющей по частотам в полосе, так как это не соответствует физической природе процесса.
Полосы частот.
При исследованиях шумов часто пользуются анализаторами с постоянной относительной полосой пропускания f2/f1=const. Полоса, у которой отношение f2/f1 = 2, называется октавой; если
f 2/f1 =1.26, то ширина полосы равна '/з октавы. При измерениях шумов используются также анализаторы с постоянной абсолютной полосой пропускания ∆f = const. Стандартные полосы указаны в таблице.
| Октавные полосы частот | Третьоктавные полосы частот | |||
| Граничные частоты, Гц | Среднегеометрические частоты, Гц | Граничные частоты, Гц | Среднегеометрические частоты, Гц | |
| 45-90 | 45-55 55-70 70-90 | |||
| 90-180 | 90-113 113-141 141-181 | |||
| 180-355 | 181-226 226-282 282-356 | |||
| 355-710 | 356-450 450-565 565-710 | |||
| 710-1400 | 710-900 900-1130 1130-1415 | |||
| 1400-2800 | 1415-1800 1800-2260 2260-2820 | |||
| 2800-5600 | 2820-3560 3560-4500 4500-5650 | |||
| 5600-11200 | 5650-7100 7100-9000 9000-11300 | |||
| 11200-22400 | 11300-14100 14100-18100 18100-22000 | |||
Уровень звукового давления
При анализе шума в качестве основной физической характеристики процесса обычно .выбирают уровень звукового давления. Уровень в полосе ∆f = 1 Гцназывается уровнем спектра и обозначается βШ. Исходя из условия некогерентности составляющих связь между уровнем в полосе частот f2 –f1 и уровнем спектра записывается в виде:
L(f2-f1) = 10lg 
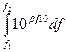 (2.35)
(2.35)
Эта формула следует из закона сложения составляющих:
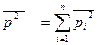 (2.36)
(2.36)
и из формулы (2.12), которую можно переписать в виде:
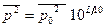 (2.37)
(2.37)
Таким образом, для конечного числа составляющих суммарный уровень звукового давления равен:
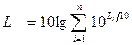 , (2.38)
, (2.38)
где n — число полос сплошного шума плюс число дискретных составляющих, или
10L/10 = 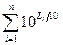 (2.39)
(2.39)
Если имеется п одинаковых составляющих с уровнем звукового давления каждой Li , то суммарный уровень звукового давления будет равен:
L = Li + 10lg n (2.40)
Чтобы облегчить вычисление суммарного уровня звукового давления при сложении “n” уровней, можно вместо формулы (2.38) воспользоваться графиком (рисунок 2.4), построенным последующему соотношению:
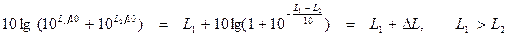 .
.
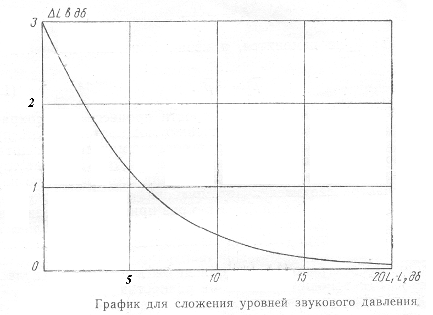
Рисунок 2.4
По оси абсцисс отсчитывается разность L1-L2 , по оси ординат - величина ∆L, которую нужно прибавить к большему уровню L1, чтобы получить суммарный уровень. Так последовательно складываются все п составляющих.
Этим же графиком удобно пользоваться при определении уровня звукового давления, развиваемого несколькими некогерентными источниками.
Пример. Определить суммарный уровень звукового давления трех компонентов, уровни каждого из которых равны L1=75 дБ, L2=62 дБ и L3=59 дБ.
Вычисляем значение L2 -L3=3 дБ; по графику находим ∆L=1,8 дБ, откуда L2”= 62+1,8=63,8 дБ; L1 – L2” =11.2 дБ; ∆L=0,3дБ; L = 75+0,3= =75,3 дБ.
Спектры, выраженные в уровнях звукового давления, обычно вычерчиваются в полулогарифмических координатах — равномерная шкала уровней и логарифмическая шкала частот.
Лекция 3
Излучение звука. Простейшие источники излучения – монополь, диполь, квадруполь – потенциал источника, колебательная скорость, звуковое давление, интенсивность звука и мощность источника. Ближнее и дальнее акустические поля .
Источник звука (излучатель) в безграничной атмосфере характеризуется звуковой .мощностью, частотным спектром и характеристикой направленности излучения.
Звуковой мощностью W называется общее количество звуковой энергии, излучаемой источником в единицу времени. Она определяется формулой
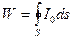 (3.1)
(3.1)
где S — замкнутая поверхность, окружающая источник звука; I0 — поток звуковой энергии (интенсивность) в направлении нормали к элементу поверхности ds. Измеряется звуковая мощность в кГм/сек или в ваттах. В .практических расчетах используется логарифмическая величина - уровень звуковой мощности, аналогичный уровню звукового давления :
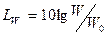 , (3.2)
, (3.2)
где W0 - постоянная величина - поток энергии с интенсивностью I0= 10-12 вт/(сек м2)= \0~13кГм/м2 сек через площадь 1 м2, то есть:
W0 =10-12вт = 10-13кГм/с (3.3)
Частотным спектром мощности излучения называется распределение излучаемой источником звуковой мощности (или уровня звуковой мощности) по шкале частот, то есть зависимость:
LWi = ψ1 (f) (3.4)
где LWi - уровень звуковой мощности в i-й полосе частот; f — средняя частота этой полосы.
Обычно допустимо считать составляющие в различных полосах частот некогерентными и суммировать их мощности энергетически. Если диапазон частот звука, создаваемого источником, ограничен, и спектр разбит на конечное число полос п, то для характеристики распределения звуковой мощности в спектре удобно пользоваться относительными спектрами звуковой мощности источника, аналогичными относительным спектрам звукового давления, введенным в предыдущем разделе:
Lw – LWi = ψ2 (f) (3.5)
где LW - суммарный уровень звуковой мощности в заданном диапазоне частот.
Удобство применения относительных спектров заключается в том, что для многих процессов можно найти такую безразмерную частоту 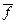 , что безразмерный относительный спектр
, что безразмерный относительный спектр
LW – LWi = ψ2 ( 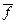 ) (3.6)
) (3.6)
может характеризовать целую группу подобных источников. При конечном числе частотных полос в спектре, по аналогии с (2.39), можно записать:
10LW/10 = 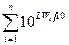 (3.7)
(3.7)
И разделив обе части на 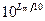 , найдем соотношение нормировки для относительных спектров:
, найдем соотношение нормировки для относительных спектров:
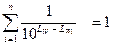 (3.8)
(3.8)
Это соотношение может служить для контроля правильности измерения или вычисления относительных спектров.
Направленность акустического излучения источника характеризуется фактором (или коэффициентом) направленности Ф, который представляет собой отношение интенсивности звука I, создаваемого источником в данной точке, к интенсивности IСФ, которую создал бы источник с такой же мощностью, но равномерно излучающий в среде без затухания по всем направлениям (т, е. обладающий сферической характеристикой направленности). То есть
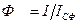 (3.9)
(3.9)
где 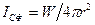 , r - расстояние от источника до точки наблюдения. Коэффициент направленности Ф — величина нормированная. Представив звуковую мощность в виде:
, r - расстояние от источника до точки наблюдения. Коэффициент направленности Ф — величина нормированная. Представив звуковую мощность в виде:
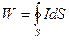 (3.10)
(3.10)
(где 5 — поверхность удаленной сферы, в центре которой находится источник) и .выразив из (3.9) значение I, получим
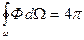 (3.11)
(3.11)
где 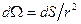 - элемент телесного угла Ω, в котором распространяется звук. Это соотношение может служить для контроля правильности вычисления или измерения характеристики направленности.
- элемент телесного угла Ω, в котором распространяется звук. Это соотношение может служить для контроля правильности вычисления или измерения характеристики направленности.
Направленность излучения может характеризоваться также отношением интенсивности или звукового давления в данной точке пространства к интенсивности или звуковому давлению на оси излучателя на таком же расстоянии от последнего.
Совокупность зависимости уровня звуковой мощности LW,, относительного спектра 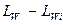 , и направленности Фi акустического излучения от режима работы и других параметров источника называется акустической характеристикой источника.
, и направленности Фi акустического излучения от режима работы и других параметров источника называется акустической характеристикой источника.
Звуковое поле (волновая зона) сформировывается лишь на некотором расстоянии от излучателя и только там можно говорить о направленности излучения; в ближней зоне около излучателя направление движения частиц среды может не совпадать с направлением потока звуковой энергии, а зависимость между давлением и скоростью может сильно отличаться от зависимости, существующей в бегущей звуковой волне.
Ближняя зона иногда называется гидродинамической, так как движение среды в ней управляется преимущественно уравнениями гидродинамики несжимаемой жидкости, а не акустики.
Действительно, в волновом уравнении (2.3) , выраженном через потенциал скорости, второй член пропорционален отношению потенциала к квадрату длины волны:
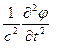 ~
~ 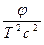 ~
~ 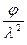 , (3.12)
, (3.12)
где Т — характерное время процесса. Первый член  уравнения пропорционален отношению потенциала к квадрату расстояния от источника до точки поля:
уравнения пропорционален отношению потенциала к квадрату расстояния от источника до точки поля:
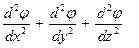 ~
~ 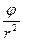 . (3.13)
. (3.13)

 При r, меньших по сравнению с λ, можно пренебречь вторым членом, и уравнение акустики переходит в уравнение гидродинамики несжимаемой жидкости:
При r, меньших по сравнению с λ, можно пренебречь вторым членом, и уравнение акустики переходит в уравнение гидродинамики несжимаемой жидкости:
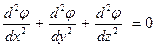 . (3.14)
. (3.14)
Таким образом, всякое решение волнового уравнения на малых расстояниях от излучателя соответствует решению уравнений движения данного тела в несжимаемой жидкости (рассматривается неподвижная среда или движущаяся, но со скоростью, существенно меньшей скорости звука). Звуковое поле неразрывно связано с гидродинамическим полем.
Точечные источники
В акустике оперируют понятием простейших (физических) источников звука, представляющих собой неподвижные материальные точки, в которых происходят попеременное втекание и вытекание жидкости в окружающую среду по тому или иному закону.
Монополь - излучатель нулевого порядка, излучающий звук равномерно по всем направлениям. Физически ему соответствует пульсирующая (расширяющаяся и сжимающаяся) сфера (рисунок 3.1а). Потенциал такого источника
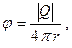 (3.15)
(3.15)
где [Q] — количество жидкости, подаваемой источником в единицу времени (расход источника) в функции аргумента (t – r/c), r - расстояние до источника
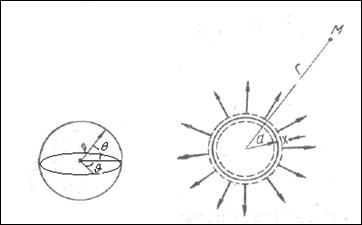
Рисунок 3.1а Простейший излучатель звука - пульсирующая сфера. Слева показана характеристика направленности
При синусоидальной зависимости от времени и расстояния потенциал сферического источника пропорционален его расходу:
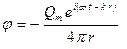 (3.16)
(3.16)
Колебательная скорость, создаваемая таким источником в направлении г, равна:
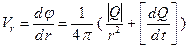 (3.17)
(3.17)
составляющие скорости, перпендикулярные к r, для этого источника 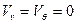 .
.
В соотношении (3.17) в квадратных скобках обозначены функции аргумента (t-r/c). Течение можно представить в виде наложения двух течений со скоростями:
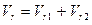 ,
,
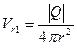 , (3.18)
, (3.18)
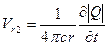
Скорость Vr1 соответствует вытеснению жидкости пульсирующей сферой, так как на поверхности сферы расход 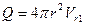 .
.
При малых “r” течение, представленное первым членом, полностью соответствует течению несжимаемой жидкости. На некотором удалении от сферы это течение отличается от существующего при аналогичных условиях в полностью несжимаемой жидкости тем, что возмущение от источника приходит в точку поля не мгновенно, а через время – r/c. Это запаздывание обусловлено сжимаемостью жидкости.
Таким образом, процесс распространения возмущения в виде звуковой волны обязательно сопровождается изменением плотности среды. Волна изменения плотности и является звуковой волной в прямом смысле этого слова; к волновому полю относятся только те составляющие скорости движения частиц среды, которые связаны с изменением ее плотности, а не вытеснением.
Вытеснение среды движущейся поверхностью излучателя приводит к изменению плотности у его поверхности, которое передается далее в виде звуковых волн. Поэтому источником волн может быть также тело с неподвижной поверхностью, на которой имеются пульсации давления, приводящие к местному переменному изменению плотности. Эти пульсации могут быть вызваны падающими на тело звуковыми волнами от другого источника, образованием вихрей у поверхности тела при его обтекании постоянным потоком и т. д. Звуковое давление выражается соотношением:
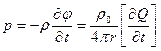 , (3.19)
, (3.19)
а изменение плотности в звуковой волне, соответствующее избыточному звуковому давлению р, будет равно:
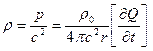 , (3.20)
, (3.20)
При большом радиусе сферы “а” волновая зона может начинаться непосредственно на ее поверхности. В этом случае вблизи поверхности сферы на расстояниях х < a волна ведет себя как почти плоская, так как там давление слабо зависит от расстояния до сферы:
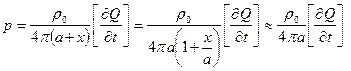 (3.21)
(3.21)
Если потенциал зависит от времени синусоидально, то колебательная скорость и давление будут равны:
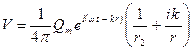 (3.22)
(3.22)
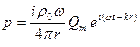 (3.23)
(3.23)
Гидродинамическая и акустическая составляющие скорости равны друг другу при kr = 1, то есть при
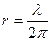 .
.
Интенсивность и мощность звука, генерируемого пульсирующей сферой, выражаются соотношениями:
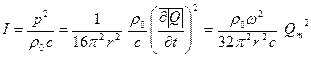 , (3.24)
, (3.24)
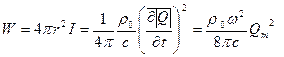 (3.25)
(3.25)
Следует обратить внимание на то, что при одном и том же расходе Qm звуковая мощность быстро растет с увеличением частоты ω. Таким образом, при сохранении неизменной амплитуды колебательной скорости на поверхности излучателя его звуковая отдача (в данном случае сферы) возрастает при увеличении отношения размера излучателя к длине звуковой волны. Это явление наблюдается у всех акустических излучателей.
Диполь – источник, образованный двумя простыми (сферическими) источниками бесконечно малых размеров с одинаковой производительностью, но работающими в противофазе и находящимися па пренебрежимо малом расстоянии друг от друга (рис. 3.16). Линия I, соединяющая источники, называется осью диполя. Направление этой линии является условным, так как положительный источник, обозначенный значком +, через половину периода станет отрицательным, и наоборот.
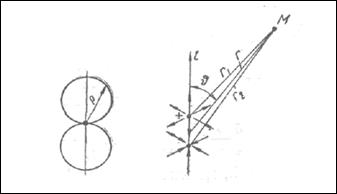
Рисунок 3.1б Простейший излучатель звука –диполь. Слева показана характеристика направленности
Поле, создаваемое диполем, соответствует полю, создаваемому .поступательно колеблющейся сферой, размеры которой меньше длины звуковых волн. Сфера может быть неподвижна, а колебания среды относительно сферы могут вызываться посторонним источником (рассеивание звука на сферическом препятствии, колебания жидкости в вихревом следе за телом и т. д.).
Потенциал диполя равен:
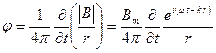 . (3.26)
. (3.26)
Выполнив дифференцирование по “t” в (3.26), получим для потенциала диполя следующее выражение:
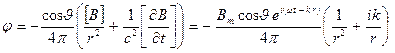 (3.27)
(3.27)
где 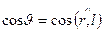 .
.
Создаваемые диполем скорости движения частиц определяются на основе соотношения (3.27):
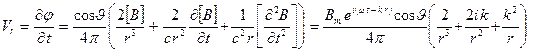 ,
,
(3.28)
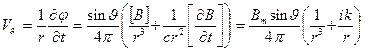 ,
,
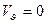 . (3.29)
. (3.29)
Давление в звуковой волне от диполя определяется выражением:
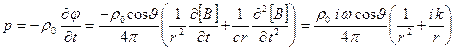 . (3.30)
. (3.30)
В случае диполя, как и для сферы, поле скорости можно представить в виде наложения совокупности скоростей ближнего .поля, ослабевающих с увеличением расстояния по закону 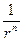 , и скорости дальнего поля, ослабевающей по закону
, и скорости дальнего поля, ослабевающей по закону 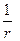 . Отличие от пульсирующей сферы заключается в том, что здесь и давление можно представить в виде комбинации членов ближнего и дальнего полей.
. Отличие от пульсирующей сферы заключается в том, что здесь и давление можно представить в виде комбинации членов ближнего и дальнего полей.
Волновую зону излучателя можно определить как область, в которой влиянием ближних членов можно пренебречь. На рисунке 3.2 показаны ближнее и дальнее поля скоростей диполя для одного из моментов времени. На рисунке видно, что направление и распределение скоростей в акустических и гидродинамических мгновенных полях могут сильно отличаться друг от друга.
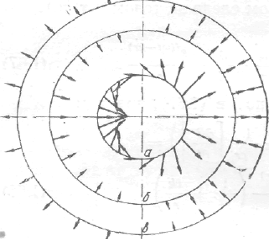
Рисунок 3.2 Ближнее (гидродинамическое) и дальнее (акустическое) поля диполя в один из моментов времени а- вблизи диполя; б - вдали; в - на расстоянии А/2 от положения б (масштабы на сферах произвольны)
Чтобы вычислить звуковую мощность диполя, нужно принимать во внимание только скорости и давления в дальнем поле, так как произведения любых ближних членов, а также произведения дальних членов на ближние пропорциональны 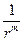 , m ≥ 3, и их интеграл по сфере неограниченно возрастающего радиуса стремится к нулю, в то время как звуковая мощность не должна зависеть от радиуса сферы, если затухания в среде не происходит. Таким образом, интенсивность звука, создаваемого диполем, направлена по радиусу и равна:
, m ≥ 3, и их интеграл по сфере неограниченно возрастающего радиуса стремится к нулю, в то время как звуковая мощность не должна зависеть от радиуса сферы, если затухания в среде не происходит. Таким образом, интенсивность звука, создаваемого диполем, направлена по радиусу и равна:
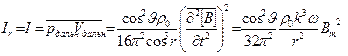 . (3.31)
. (3.31)
В силу круговой симметрии излучения относительно оси диполя звуковая мощность равна:
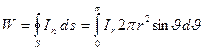 (3.32)
(3.32)
Подставив в последнее соотношение выражение для Ir из (3.31) и выполнив интегрирование, получим:
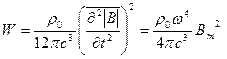 (3.33)
(3.33)
Диполь можно представить в виде вектора В, направление которого совпадает с осью диполя l. Тогда физические величины в дальней звуковой волне будут пропорциональны проекции этого вектора на радиус r, соединяющий рассматриваемую точку с центром диполя, а мощность можно считать состоящей из суммы мощностей компонентов:
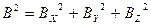 ,
,
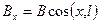 ,
, 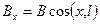 ,
, 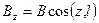 ,
,
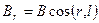 =
= 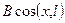 +
+ 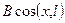 +
+ 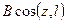 (3.34)
(3.34)
Дипольное излучение характерно для аэродинамического шума и других шумов, генерация которых обусловлена силовым воздействием на среду, таких как шум лопаточных машин газотурбинного двигателя, шум воздушных винтов, шум обтекания планера воздушного судна.
Квадруполь, - источник, составленный из двух равных и противоположных по знаку диполей (см. рисунок 3.1в) так, что механические силы и моменты, действующие на квадруполь, равны нулю независимо от закона изменения во времени производительности “Q” каждого источника, составляющего квадруполь. Оси l1 и l2 диполей могут располагаться под произвольным углом друг к другу ε. Частными случаями будут поперечный квадруполь, у которого оси составляющих диполей расположены под .прямым углом, и продольный квадруполь с осями на одной прямой.
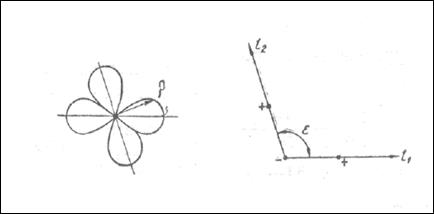
Рисунок 3.1в Простейший излучатель звука –квадруполь. Слева показана характеристика направленности
Потенциал квадруполя
φ 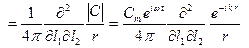 (3.35)
(3.35)
или
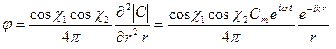 (3.36)
(3.36)
Из последнего выражения видно, что, в отличие от диполя, квадруполь характеризуется не одним, а двумя направляющими косинусами, где С - момент квадруполя.
В дальнем звуковом поле, пренебрегая в (3.35) и (3.36) членами, убывающими как 1/rn, где n ≥ 2, получим следующие выражения для колебательной скорости, звукового давления и интенсивности звука:
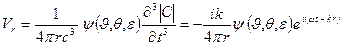 (3.37)
(3.37)
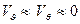 ,
,
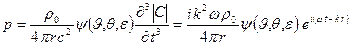 , (3.38)
, (3.38)
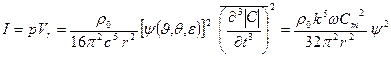 , (3.39)
, (3.39)
где ψ- функция координатных узлов и скоса диполя, которую нетрудно найти из приведенных выше формул; Ст — амплитуда момента квадруполя.
Выполнив интегрирование по сфере, получим общую формулу для мощности акустического излучения квадруполя:
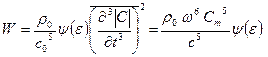 , (3.40)
, (3.40)
здесь ψ(ε)— функция конфигурации квадруполя. В гидродинамической ближней зоне квадруполя скорость убывает с расстоянием, как 1/r4. Квадрупольное излучение характерно для такого важного в современной технике источника шума, как турбулентная струя газа (реактивная струя ГТД).
О границе дальней волновой зоны
Каждый элемент поверхности “dS” колеблющегося тела конечной величины можно считать источником сферических звуковых волн. Расход такого элементарного источника равен:
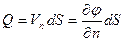 , (3.41)
, (3.41)
где n - внешняя нормаль к элементу поверхности dS; Vn - нормальная к поверхности составляющая скорости. Потенциал, создаваемый в какой-либо точке пространства М телом с произвольным распределением колебательных скоростей по поверхности, будет равен сумме потенциалов, создаваемых элементарными источниками.
Дальней (волновой) зоной .излучателя, размеры которого существенно меньше размеров волны, следует считать область, где уже сформировалась его характеристика направленности, и, следовательно, в выражениях для скорости и давления можно пренебречь членами, обратно пропорциональными расстоянию в степени выше второй включительно. Из полученных для простого источника диполя и квадруполя выражений видно, что это условие соблюдается, если расстояние “r”удовлетворяет условию: 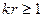 .
.
Необходимо, чтобы разность длин лучей, проведенных в точку наблюдения из центра излучателя, размеры которого существенно больше размеров .волн, и его периферии, мало отличалась от разности, которая существовала .бы для бесконечно удаленной точки, так как именно эта разность длин приводит к сформированию характеристики направленности излучателя больших размеров. Для точки наблюдения, расположенной на оси излучателя с поперечным размером “D” (рисунок 3.3), это соответствует условию
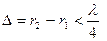 . (3.42)
. (3.42)
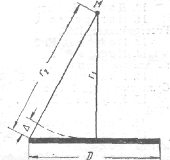
Рисунок 3.3
Поскольку 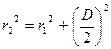 и
и 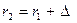 , то, пренебрегая величиной ∆2 по сравнению с
, то, пренебрегая величиной ∆2 по сравнению с 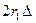 , получим условие существования дальней волновой зоны:
, получим условие существования дальней волновой зоны:
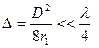 (3.43)
(3.43)
Другими словами, в дальнем акустическом поле должно выполняться условие: 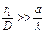 , где а = D/2 - радиус излучателя. Для излучателя больших размеров расстояние, выраженное в диаметрах излучателя, должно быть больше радиуса излучателя, выраженного в длинах волн.
, где а = D/2 - радиус излучателя. Для излучателя больших размеров расстояние, выраженное в диаметрах излучателя, должно быть больше радиуса излучателя, выраженного в длинах волн.
Практически область волновой зоны можно найти, измеряя уровни звукового давления на различных, расстояниях от излучателя. До тех пор пока на лучах, соединяющих точку наблюдения с центром излучателя, соблюдается условие:
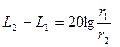 (3.45)
(3.45)
можно считать, что практически имеет место волновая зона. Иногда оказывается, что граница волновой зоны на различных лучах соответствует разным расстояниям.
Лекция 4
Пространственно-временные и спектральные характеристики шума самолетов на местности на режимах взлета и захода на посадку. Соотношение между источниками шума на местности современных самолетов. Описание и основные характеристики шума современных ТРДД в статических условиях. Источники шума ТРДД и общая характеристика источников шума.
Дата добавления: 2016-04-19; просмотров: 2581;
